Por qué los ingenieros químicos deberían conocer ANOVA
- Detalles
- Categoría: Minitab
- Visto: 8167

Por Joshua Zable.
En términos generales, si es ingeniero químico, probablemente estará desarrollando y diseñando procesos de fabricación de productos químicos. A diferencia de otros ingenieros, eso significa que es posible que deba aplicar los principios de la química, la biología, la física y las matemáticas para resolver problemas que involucran la producción o el uso de productos químicos, combustibles, medicamentos, alimentos y muchos otros productos. Con todo ese tiempo dedicado a las ciencias, si no ha dedicado tanto tiempo a la estadística como desearía, no se preocupe, ¡Minitab está aquí! Ahora, hablemos de por qué el análisis de varianza (ANOVA) puede ser el arma secreta de un ingeniero químico.
POR QUÉ DEBERÍA CONOCER ANOVA
Muchas aplicaciones industriales involucran experimentos donde el objetivo es comprender si los grupos son diferentes. En términos estadísticos, consideramos un factor, digamos el tipo de catalizador, y queremos entender si los niveles de ese factor, digamos catalizador 1, catalizador 2, catalizador 3 y catalizador 4, son significativamente diferentes estadísticamente entre sí. Cuando las mediciones en los grupos son continuas y se cumplen otras suposiciones, utilizamos ANOVA para comparar las medias de los grupos. En cierto sentido, el nombre "Análisis de varianza" es inapropiado, porque estamos interesados en comparar las medias de los grupos. Sin embargo, al analizar la variación en los datos dentro de los niveles de grupo y entre los grupos, podemos determinar si las medias del grupo son estadísticamente diferentes.
ANOVA prueba la hipótesis nula de que las medias de la población (señaladas con el símbolo µ) son todas iguales. Estimaremos las medias poblacionales utilizando las medias muestrales. Si se rechaza esta hipótesis nula, concluimos que las medias de la población no son todas iguales.
La hipótesis nula:
Ho: µCatalizador 1 = µCatalizador 2 = µCatalizador 3 = µCatalizador 4
.png)
En lenguaje sencillo, asumimos que las medias son todas iguales en todos los grupos, y recopilamos evidencia en contra de eso, lo que significa que si observamos grandes diferencias de medias entre estas medias, estaremos más seguros al rechazar esa creencia y al asumamir que hay diferencias dentro de los niveles de grupo.
EJEMPLO DE ANOVA DE UN FACTOR
Imagine que una ingeniera química quiere comparar el rendimiento del producto utilizando cuatro catalizadores diferentes. Ella calentará el catalizador con el producto para obtener una reacción. Utilizando ANOVA, la ingeniera puede determinar si el rendimiento del producto usando diferentes catalizadores difiere significativamente.
Primero, la ingeniera recopila sus datos, como se puede ver a continuación.
A continuación, la ingeniera corre un ANOVA de un solo factor.
El p-valor para el ANOVA de rendimiento del producto es pequeño, lo que indica que existe una probabilidad muy pequeña de que hubiéramos observado estos resultados si la hipótesis nula es cierta, es decir, que las medias del catalizador son todas iguales. Debido a que el valor p es menor que un nivel de significancia del 5% (estamos usando un alfa = 0.05), rechazamos la hipótesis nula. Concluimos que t, el rendimiento medio del producto, difiere entre los grupos catalizadores.

La ingeniera sabe que algunas de las medias del grupo son diferentes. La siguiente pregunta lógica es, ¿cuáles?
USO DEL MÉTODO DE TUKEY PARA REALIZAR LAS COMPARACIONES MÚLTIPLES
Si bien ANOVA nos enseñó que algunas de las medias del grupo son diferentes, la ingeniera necesita una comparación más profunda para comprender qué medias de grupo son diferentes. Minitab proporciona "Comparaciones" por esta misma razón. En nuestro ejemplo, la ingeniera química usa las comparaciones de Tukey para probar formalmente las diferencias entre los pares de grupos, para comprender cuáles son estadísticamente significativamente diferentes.
La prueba de comparación múltiple de Tukey es la prueba más conservadora de varias pruebas que se pueden utilizar para determinar qué medias entre un conjunto de medias difieren del resto. El método de Tukey se usa después de ANOVA (por lo que es posible que escuche que se hace referencia al método como una prueba post hoc) y se puede utilizar para crear intervalos de confianza para todas las diferencias por pares entre las medias de los niveles de factor mientras se controla la tasa de error familiar a un nivel que usted especifique.
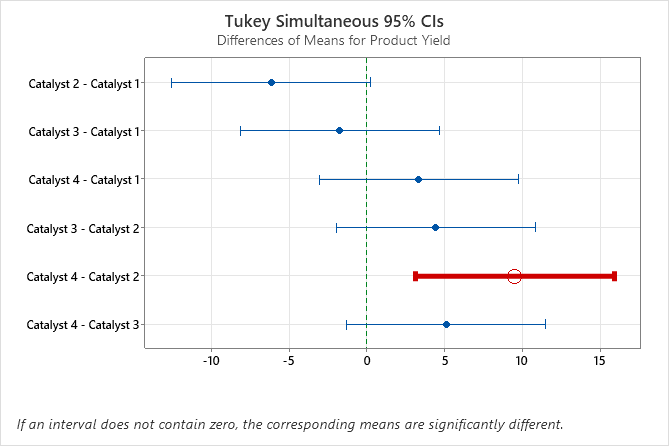
En nuestro ejemplo, el gráfico que incluye los intervalos de confianza simultáneos de Tukey muestra que el intervalo de confianza para la diferencia entre las medias de los Catalizadores 2 y 4 es de 3,114 a 15,886. Este rango no incluye cero, lo que indica que la diferencia entre estas medias es significativa. La ingeniera puede usar esta estimación de la diferencia para determinar si la diferencia es prácticamente significativa.
Por el contrario, los intervalos de confianza para los pares de medias restantes incluyen todos cero, lo que indica que las diferencias no son significativas.
¿POR QUÉ NO CORRER UN MONTÓN DE PRUEBAS T PARA IDENTIFICAR DIFERENCIAS?
Es una gran pregunta, ¡y surge mucho! La respuesta tiene que ver con el riesgo de cometer un error, específicamente, el riesgo de concluir incorrectamente que existe una diferencia estadísticamente significativa, que es lo que llamamos nuestro riesgo alfa. Cuando realizamos una prueba, hay un 5% de probabilidad de que digamos que hay una diferencia, cuando en realidad no la hay. Para los 4 catalizadores, ¡eso daría como resultado 6 pruebas t!
¿Cuál es la probabilidad de observar al menos un resultado significativo debido al azar?
P(al menos un resultado significativo) = 1 - P (sin resultados significativos)
= 1 - (1 - 0.05)6
≈ 0,264
Entonces, con 6 pruebas consideradas, tenemos un 26% de posibilidades de observar al menos un resultado significativo, incluso si todas las pruebas no son realmente significativas. Las pruebas post hoc controlan la tasa de error de los experimentos; para decirlo de manera más simple, queremos asegurarnos de que la probabilidad de que declaremos incorrectamente que cualquier par de catalizadores es diferente permanezca en el 5%. ¡Eso es exactamente lo que hace la prueba de Tukey por nosotros!
LAS RESPUESTAS ESTÁN EN ANOVA
El uso de ANOVA permite a un ingeniero químico probar mezclas para ver si los resultados son estadísticamente significativos. Igualmente importante, también puede determinar si todo el grupo es diferente o quizás solo un subsegmento del grupo utilizando pruebas de comparación. En nuestro ejemplo, solo el catalizador 2 y el catalizador 4 tienen diferencias estadísticamente significativas con respecto al rendimiento del producto. Con base en esta información, la ingeniera química puede comenzar a mirar los otros catalizadores para determinar qué catalizador es el más rentable, tiene la vida útil más larga o es más fácil de acceder sabiendo que producirá una cantidad similar de producto.

