- Detalles
- Categoría: NAG
- Visto: 5226
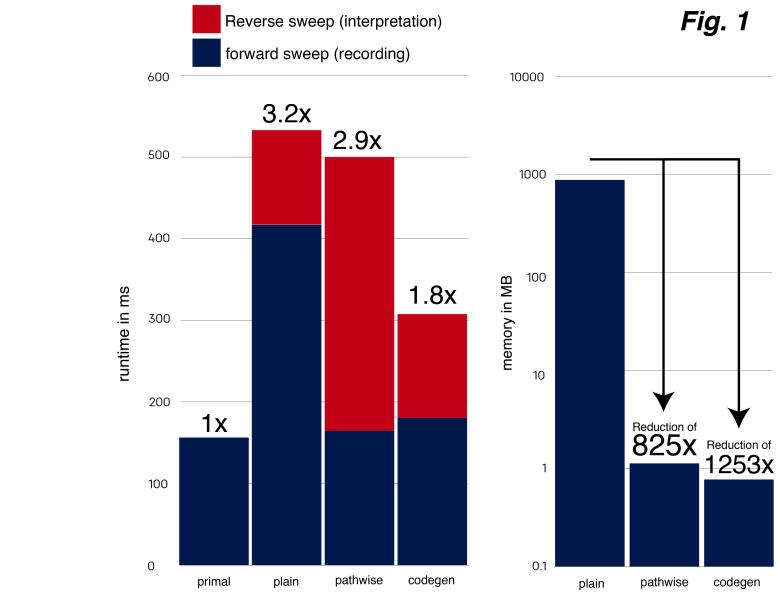
La diferenciación automática adjunta (AAD) es una técnica informática para calcular derivadas. Usada correctamente, AAD calcula las derivadas mucho más rápido y con mucha más precisión que los métodos alternativos.
NAG continúa innovando en el área de diferenciación automática a través de su colaboración con científicos informáticos líderes del RWTH Aachen y más allá con la última actualización de su producto de vanguardia. NAG proporciona una biblioteca de encabezados de C++ AD rica en funciones, completa y potente, que incluye Adjoint AD, denominada dco/c++, que ha abordado las necesidades de los clientes durante más de una década.
La herramienta de diferenciación automática dco/c++ de NAG ahora incluye:
Generación de código
¿Qué es?
Una tecnología híbrida que combina la eficiencia de transformación de fuente con la flexibilidad y…
- Detalles
- Categoría: NAG
- Visto: 5226
Uno de los algoritmos clave para abordar problemas generales de optimización no lineal con restricciones es un método de programación cuadrática secuencial (SQP) de conjunto activo. Es un caballo de batalla para muchos resolvedores comerciales y de código abierto. Las Librerías NAG® ofrecen una versión de última generación dentro de Optimization Modeling Suite. Complementa el método del punto interior (IPM) de NAG y otros métodos especializados para la optimización no lineal, como la optimización libre de derivadas (DFO) o el método de primer orden.
- Detalles
- Categoría: NAG
- Visto: 3976
DekaBank quería una mejor gestión de riesgos, precios más precisos y respaldar el negocio de derivados en expansión del banco, todo sin aumentar los costes informáticos. Fue entonces cuando recurrieron a la diferenciación automática (AD) y, en particular, a la diferenciación automática adjunta (AAD). Después de comparar tres herramientas, DekaBank eligió la solución AD de NAG, NAG® DCO/C++.
DCO/C++
Herramienta de software AD para calcular sensibilidades de códigos en C++
- Incorpora más de 15 años-persona de I+D, muchos de los cuales han requerido investigación original.
- Es una herramienta de sobrecarga de operadores con una API ingeniosa: la herramienta es fácil de aprender, fácil de usar, se puede aplicar rápidamente a una base de código y se integra fácilmente con entornos de compilación y prueba.
- Se pueden calcular derivados de orden…
- Detalles
- Categoría: NAG
- Visto: 3881
La última Mark de la librería NAG® ya está disponible para su descarga. Mark 27.3 presenta un resolvedor simbólico de Matriz de Correlación más Cercana (NCM), FEAST Eigensolver y más resolvedores de diferenciación automática (AD) de segundo orden.
Destacamos el nuevo solucionador NCM para calcular el adjunto simbólico de la matriz de correlación más cercana (NCM). Calcular derivadas del NCM permite encontrar sensibilidades a los datos de entrada. El adjunto simbólico calcula la derivada matemáticamente, lo que da como resultado una rutina que es 70 veces más rápida y utiliza 2500 veces menos memoria que el adjunto algorítmico. Se accede al adjunto simbólico a través de un nuevo modo para el solucionador g02aa. Anteriormente, esto se podía hacer en la Librería NAG AD calculando el adjunto algorítmico, que diferenciaba el…