Este primer artículo de la serie dentro de The NAG Optimization Corner está dedicado a brindar orientación sobre cómo elegir la herramienta de optimización adecuada para un problema dado y demostrar las consecuencias de una elección inapropiada.

En NAG sabemos que elegir la herramienta de optimización adecuada puede ser una tarea bastante difícil y que el proceso, en ocasiones, puede parecer confuso. Una parte de nuestras solicitudes de servicio al cliente tratan este mismo tema. La mayoría de las veces, las consultas comienzan con la misma pregunta: "¿Por qué falla el resolvedor?" y, con bastante frecuencia, una inspección más detallada revela que se ha elegido el resolvedor incorrecto o que el modelo podría mejorarse significativamente. Si bien esta publicación aborda el primero, apreciamos que construir un modelo bueno o incluso adecuado puede no ser nada fácil, este tema se revisará en una próxima publicación de esta serie.

En esta publicación, mostramos dos ejemplos que ilustran la importancia de elegir el resolvedor adecuado y concluimos con algunas observaciones importantes.

Diferentes problemas y diferentes resolvedores.

A diferencia de las gorras de béisbol, una misma talla no sirve para todos cuando se trata de resolver problemas de optimización. De hecho, es una práctica recomendada intentar siempre primero el ajuste más ajustado posible. Tomemos, por ejemplo, el siguiente caso: resolver un problema de programación lineal (LP) utilizando un resolvedor de programación no lineal general (NLP) en lugar del resolvedor LP ajustado. La herramienta NLP será más cara y menos robusta que el resolvedor de LP ajustado especializado que comprende y explota la linealidad del problema.

A continuación, mostraremos por qué es esencial comprender y explotar la estructura subyacente de un problema de optimización y combinarlo con un resolvedor que pueda aprovecharlo.

Comencemos por presentar rápidamente las distintas partes que componen un problema de optimización. Un problema se compone de variables, una función objetivo y restricciones. Los diferentes tipos de variables, objetivos y restricciones definen diferentes clases de problemas. La Introducción al capítulo Optimización E04 de NAG ofrece una descripción completa de las diversas clases de problemas de optimización y los resolvedores recomendados para su uso.

Calibraciones costosas

Los problemas de calibración (ajuste de datos, regresión) generalmente se expresan en términos de mínimos cuadrados lineales (LSQ) o no lineales (NLN-LSQ) con la tarea de minimizar la suma de los cuadrados de los residuos. Las funciones residuales, r_I(x), representan el error entre la predicción del modelo y los datos, mientras que la función objetivo se denota como

.

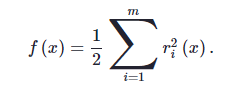
Para obtener más información sobre la optimización de mínimos cuadrados, consulte la documentación de NAG sobre optimización.

Se realizó el siguiente experimento, resolvimos un lote de 39 problemas NLN-LSQ no restringidos y comparamos un resolvedor NLN-LSQ especializado con un resolvedor NLP de propósito general. Los resultados de la evaluación comparativa, que se muestran en la Figura 1, muestran que NLN-LSQ es notablemente más rápido. En promedio, el resolvedor especializado NLN-LSQ ofrece una velocidad 1,8 veces mayor que el resolvedor general de NLP, con un 20% de los problemas resueltos al menos 5 veces más rápido. Como revelan los últimos problemas 32–39, a veces el resolvedor de PNL puede superar al especializado debido a factores como el punto de partida que favorece a un método en particular sobre otros. Esto también destaca la importancia de probar más de un resolvedor.

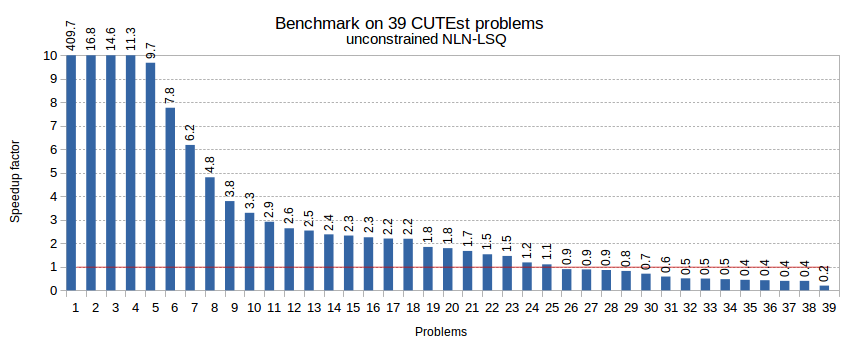
Figura 1. Comparativas de referencia en más de 39 problemas CUTEst NLN-LSQ que comparan los rendimientos de los resolvedores NLN-LSQ y NLP. La altura de la barra vertical representa el factor de aceleración medido como la relación de tiempo NLP / tiempo NLN-LSQ.

El factor de aceleración más importante para el resolvedor NLN-LSQ está en cómo se aproxima el hessiano. Más detalladamente, el problema se define como

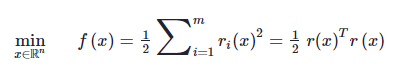
Objetivo de mínimos cuadrados no lineal

con el siguiente gradiente (primeras derivadas) y hessiano (segundas derivadas)

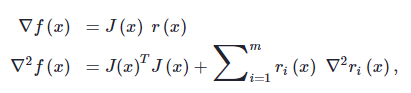
donde J(x) es el jacobiano de los residuos. Ahora, el hessiano resulta ser el producto matriz-matriz del transpuesto del jacobiano por sí mismo (también conocido como la matriz de Gauss-Newton) y una suma de m residuos hessianos. Si el problema tiene una buena solución de ajuste (pequeños residuos r_I(x)) luego cerca de una solución la segunda parte que involucra la suma de los residuos hessianos, 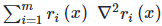, pueden considerarse insignificantes y, por lo tanto, se omiten. Este último hecho es muy importante, ya que evaluar m hessianos individuales pueden ser extremadamente caro.

Las LSQ dedicadas son generalmente más rápidas porque conocen y explotan estos hechos importantes y, por lo tanto, pueden aproximar con éxito las segundas derivadas utilizando solo las primeras derivadas de los residuos. Mientras que los resolvedores NLP genéricos no pueden hacer estas suposiciones clave y no se aprovechan de ellas.

Compromiso: NLP para resolver QP

Los resolvedores de NLP de propósito general son capaces de resolver una gran variedad de clases de problemas con el compromiso de no explotar la estructura del problema subyacente. Solo deben usarse cuando no se dispone de resolvedores especializados. En el siguiente ejemplo, ilustramos tal compensación resolviendo un lote de 50 QP convexos (problemas de programación cuadrática) y comparando el costo incurrido en el uso del resolvedor de NLP general nlp2_sparse_solve (e04vh) en lugar del cuadrático convexo especializado nlp2_sparse_solve (e04nq) donde ambos resolvedores son métodos de conjuntos activos. Los resultados computacionales visualizado en la Figura 2 muestran que el resolvedor QP e04nq es en promedio 2,3 veces más rápido que el resolvedor de NLP e04vh y al menos 5 veces más rápido en el 28% de los problemas.

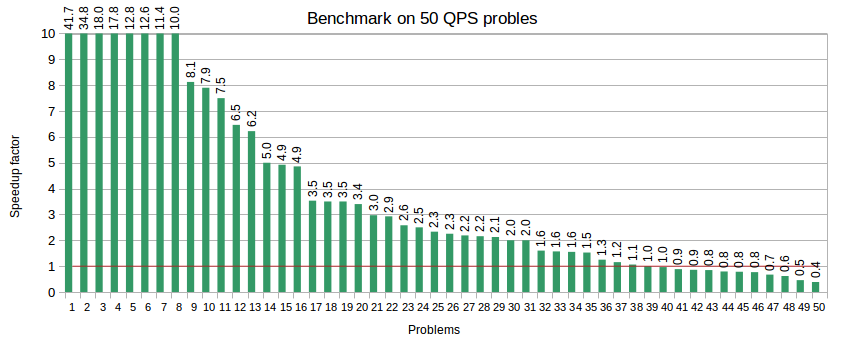
Figura 2. Comparativas de referencia en 50 problemas convexos de QP comparando el rendimiento de los resolvedores de QP y NLP. La altura de la barra vertical representa el factor de aceleración medido como la relación de tiempo NLP / tiempo QP.

El mayor factor de aceleración es esencialmente que e04nq, el resolvedor especializado, se adapta a la estructura QP y aprovecha el hecho de que el hessiano (segundas derivadas) es constante para todoa x. Mientras que el resolvedor general e04vh no tiene acceso a la misma información, ya que no solicita segundas derivadas. En general, los resolvedores de NLP que pueden usar derivadas de segundo orden tendrán un alto costo computacional por iteración, requiriendo, por ejemplo, costosas factorizaciones del hessiano o actualizaciones parciales de una aproximación al mismo, potencialmente en cada iteración.

Cosas para recordar

En esta artículo, presentamos dos ejemplos que ilustran la compensación de usar resolvedores de optimización genéricos para resolver problemas que tienen una estructura subyacente. Los resultados numéricos muestran que los resolvedores especializados son preferibles a los genéricos.

• Elija el resolvedor de optimización adecuado. Es ventajoso tomarse el tiempo para comprender la estructura subyacente del problema y elegir el resolvedor que se ajuste más a los requisitos. Es por eso que la biblioteca NAG le ofrece una gran variedad de resolvedores de optimización.
• El resolvedor especializado ofrece un mejor rendimiento (tiempo de solución) pero también robustez y precisión.
• Elegir el resolvedor adecuado no siempre es una tarea fácil. Aquí en NAG, siempre estamos listos para ayudarle. Tenemos una mesa de soporte amigable y muchos recursos en línea a su disposición, como los diagramas de árbol de decisiones fáciles de explorar para ayudarlo a elegir la herramienta de optimización adecuada.
• Si hay dos o más resolvedores que se ajustan a su problema, la experimentación numérica ayuda a elegir el mejor. Abordaremos este tema en una próxima publicación.

Nuestra próxima publicación de esta serie tratará sobre problemas densos y escasos.