COMSOL Uncertainty Quantification Module 6.4
DESCRIPCIÓN
El módulo de cuantificación de incertidumbre, Uncertainty Quantification Module, se utiliza para comprender el impacto de la incertidumbre del modelo: cómo las cantidades de interés dependen de las variaciones en las entradas de un modelo. Proporciona una interfaz general para la detección, el análisis de sensibilidad, la propagación de la incertidumbre y el análisis de fiabilidad.
Uncertainty Quantification Module puede probar de manera eficiente la validez de los supuestos del modelo, simplificar los modelos de manera convincente, comprender la entrada clave de las cantidades de interés, explorar la distribución de probabilidad de las cantidades de interés y descubrir la fiabilidad de un diseño. La garantía de la corrección del modelo y una mayor comprensión de las cantidades de interés ayudan a reducir los costes de producción, desarrollo y fabricación.
SECTORES
Uncertainty Quantification Module se puede utilizar con productos de toda la suite de productos COMSOL para analizar incertidumbres en simulaciones de ingeniería electromagnética, estructural, acústica, de flujo de fluidos, térmica y química. Puede combinarlo con el módulo de importación de CAD, el módulo de diseño o cualquiera de los productos LiveLink™ para CAD.
CARACTERÍSTICAS
Parámetros de entrada y cantidades de interés
Cuando se arranca un estudio de cuantificación de incertidumbre se define un conjunto de parámetros de interés en términos de una solución del modelo COMSOL®. De esta forma, las cantidades de interés son funciones de los parámetros de entrada.
En el caso de un análisis estructural, las cantidades de interés pueden ser el desplazamiento máximo, la tensión o el ángulo de deflexión. Para un análisis de transferencia de calor o CFD, las cantidades de interés pueden ser la temperatura máxima, la pérdida total de calor o la tasa de flujo total del fluido. Para una simulación electromagnética, pueden ser resistencia, capacitancia o inductancia. Dado que Uncertainty Quantification Module es aplicable a cualquier modelo físico calculado con el software COMSOL Multiphysics®, así como a cualquier expresión matemática de varias magnitudes de campo resueltas, las opciones que pueden ser valor de interés son infinitas.
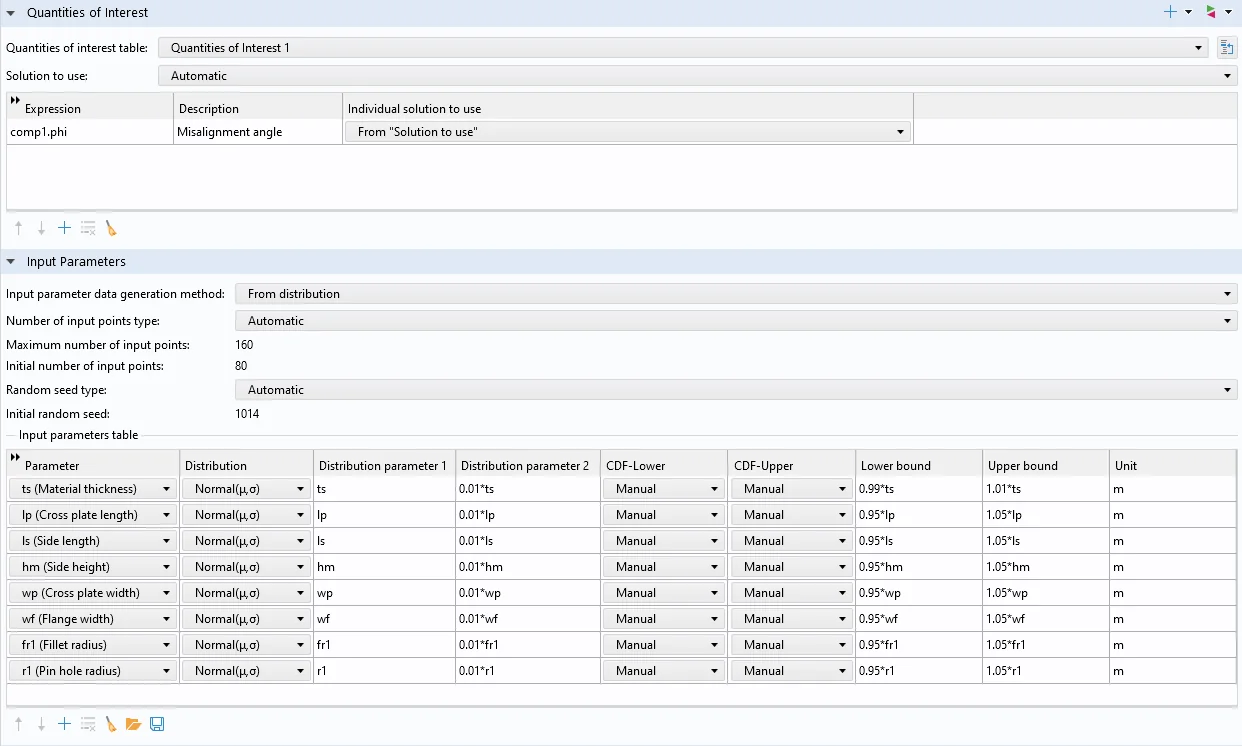
Los ajustes para los parámetros de entrada y los valores de interés.
Cualquier entrada de modelo incierta, ya sea una configuración física, una dimensión geométrica, una propiedad de material o una configuración de discretización, puede tratarse como un parámetro de entrada, y cualquier salida del modelo puede utilizarse para definir las cantidades de interés.
Screening
El tipo de estudio Screening, MOAT implementa un método de cribado global ligero que proporciona una medida cualitativa de la importancia de cada parámetro de entrada. El método se basa puramente en las muestras, utiliza el método de Morris one-at-a-time (MOAT), y requiere un número relativamente pequeño de evaluaciones del modelo COMSOL. Esto lo convierte en un método ideal cuando el número de parámetros de entrada es demasiado grande para permitir estudios de cuantificación de incertidumbre más costosos desde el punto de vista computacional.
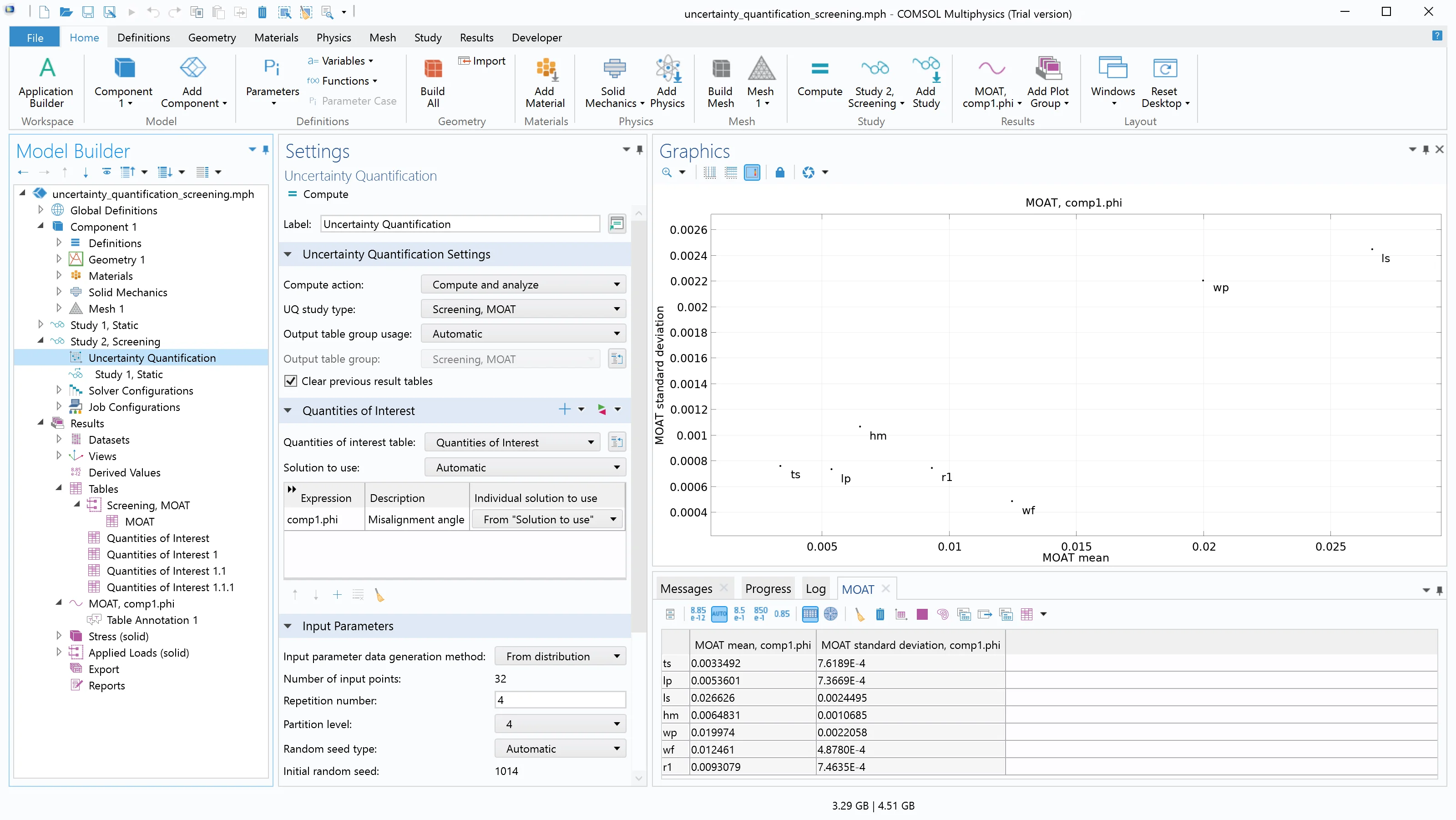
Se realiza un análisis Screening de la media y desviación estándar MOAT para un valor de interés, con siete parámetros de entrada. Un diagrama de dispersión MOAT se muestra como resultado.
Para cada valor de interés, este método MOAT calcula la media MOAT y la desviación estándar MOAT para cada parámetro de entrada. Estos valores se presentan en un diagrama de dispersión MOAT. La clasificación de la media MOAT y las desviaciones estándar MOAT dan la importancia relativa de los parámetros de entrada. Un valor alto de la media MOAT implica que el parámetro influye significativamente en el valor de interés. Un valor alto de la desviación estándar MOAT implica que el parámetro es influyente y que está interactuando fuertemente con otros parámetros o que tiene una influencia no lineal, o ambas cosas.
Análisis de sensibilidad
El tipo de estudio Análisis de sensibilidad/Sesitivity Analysis se utiliza para calcular la sensibilidad de los valores de interés con respecto a los parámetros de entrada. Este tipo de estudio incluye dos métodos: el de Sobol y el de correlación.
El método de Sobol analiza toda la distribución de parámetros de entrada y descompone la varianza de cada cantidad de interés en una suma de contribuciones de los parámetros de entrada y sus interacciones.
Para cada parámetro de entrada, el método de Sobol calcula los índices de Sobol. El índice de Sobol de primer orden muestra la varianza de una cantidad de interés atribuida a la varianza de cada parámetro de entrada individualmente. El índice de Sobol total muestra la varianza de una cantidad de interés atribuida a la varianza de cada parámetro de entrada y su interacción con los otros parámetros de entrada. Los índices de Sobol para cada cantidad de interés y todos los parámetros se presentan en un diagrama de Sobol dedicado donde los histogramas se ordenan por índice de Sobol total. La cantidad de interés es más sensible al parámetro de entrada con el índice de Sobol total más alto. La diferencia entre el índice de Sobol total y el índice de Sobol de primer orden para un parámetro de entrada mide el efecto de la interacción entre esta entrada y otras.
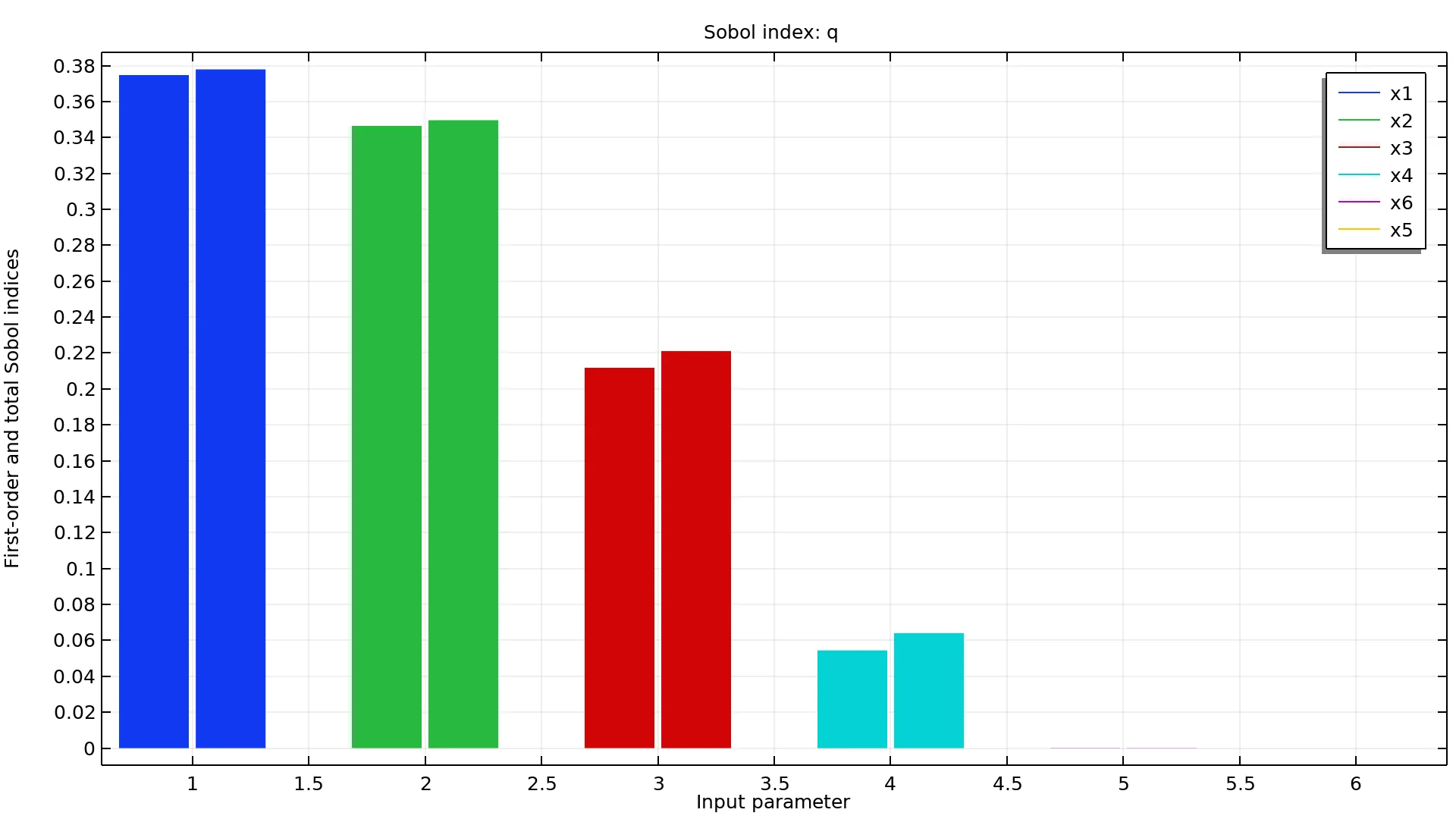
Un gráfico de índice de Sobol para un valor de interés 'q' utilizando 6 parámetros de entrada donde cada par de barras del mismo color representa un parámetro de entrada. La bara izquierda de cada par representa el índice Sobol de primer orden y la de la derecha el índice Sobol total.
En comparación con el método de selección, el análisis de sensibilidad se utiliza para analizar cuantitativamente cómo las incertidumbres en los valores de interés se distribuyen entre los diferentes parámetros de entrada. Este método requiere más recursos computacionales ya que el cálculo de índices de Sobol precisos se basa en un modelo sustituto de alta calidad.
El método de correlación calcula la relación lineal y monótona entre cada parámetro de entrada y los valores de interés. Para el análisis de sensibilidad basado en el método de correlación se calculan cuatro tipos de correlaciones: correlación bivariada, bivariada clasificada, parcial o correlación parcial clasificada.
Propagación de la incertidumbre
El tipo de estudio Propagación de la incertidumbre se utiliza para analizar cómo las incertidumbres de los parámetros de entrada se propagan a cada valor de interés mediante la estimación de su función de densidad de probabilidad (PDF). La física subyacente que asigna los parámetros de entrada a los valores de interés a través de las evaluaciones del modelo de COMSOL Multiphysics® es imposible de calcular analíticamente para la mayoría de las aplicaciones.
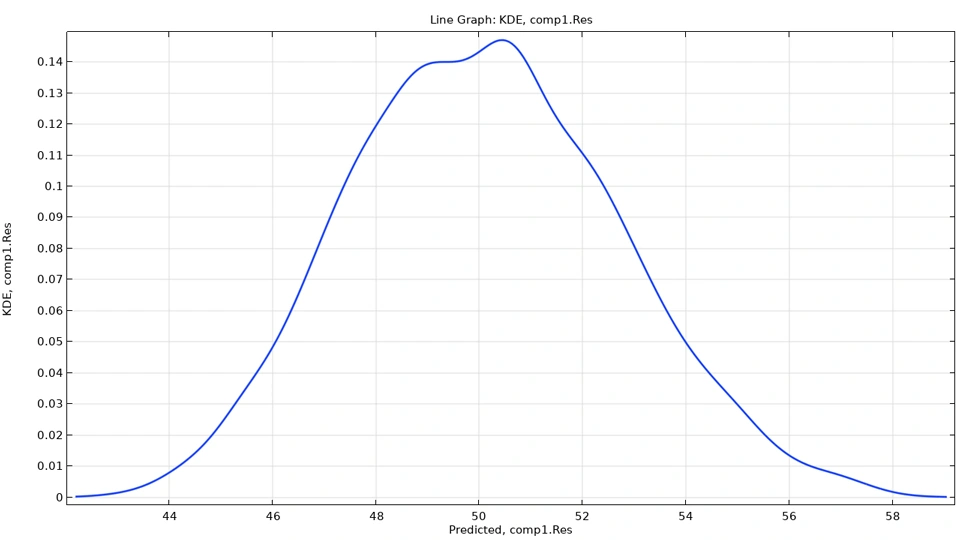
Por esta razón, es necesario un análisis de Monte Carlo para aproximar las PDF. Similar al método de Sobol, se utiliza un modelo sustituto para reducir drásticamente el coste computacional del análisis de Monte Carlo. Para cada valor de interés, se realiza una estimación de densidad kernel (KDE) y se visualiza como un gráfico, como una aproximación de la PDF. Además, en base a este análisis, una tabla de intervalos de confianza brinda, para cada valor de interés, la media; Desviación Estándar; mínimo; máximo; y los valores límite inferior y superior correspondientes a niveles de confianza del 90%, 95% y 99%.
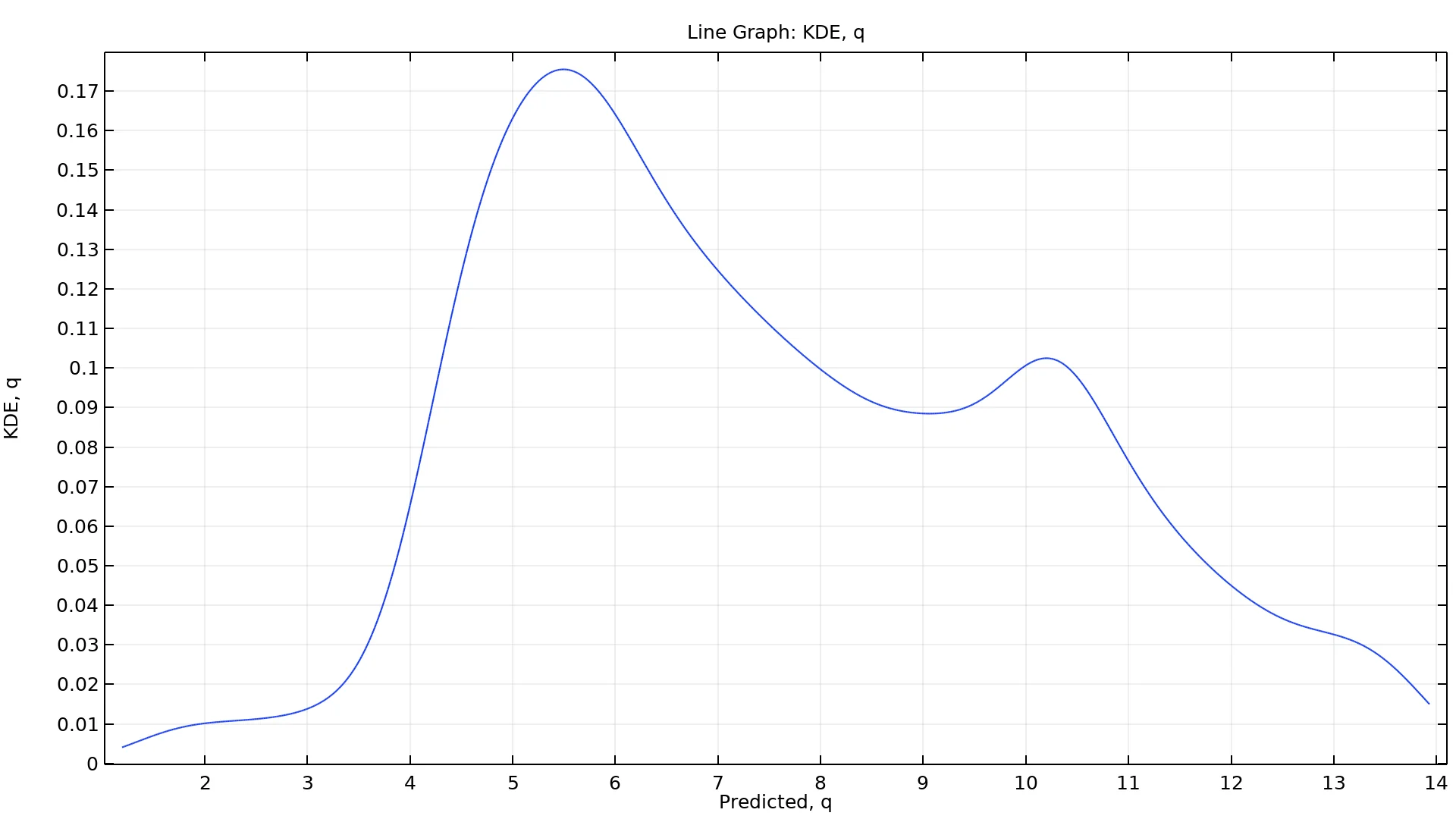
Un gráfico de estimación de la densidad kernel para el valor de interés q.
Análisis de fiabilidad
En comparación con otros tipos de estudios de cuantificación de la incertidumbre que investigan la incertidumbre general de los valores de interés, el método Reliability analysis, EGRA aborda una pregunta más directa. Dado un diseño nominal y algunas entradas inciertas específicas, ¿cuál es la probabilidad de que el diseño falle? La falla puede ser una falla completa del diseño, pero también puede expresarse en términos de un criterio de calidad.
Para garantizar la fiabilidad, el enfoque tradicional de modelado y simulación es utilizar márgenes de seguridad y escenarios del peor de los casos. Con un análisis de fiabilidad adecuado es posible evitar la sobreestimación y la subestimación, ya que se pueden realizar estimaciones de la probabilidad real. Se puede obtener una estimación aproximada de la tabla de intervalos de confianza de la propagación de la incertidumbre para cada valor de interés. Pero con el análisis de fiabilidad, puede definirse un criterio de fiabilidad más sofisticado basado en combinaciones de los valores de interés y los umbrales correspondientes. El método de análisis de fiabilidad global eficiente (EGRA) utilizado para el estudio de análisis de fiabilidad dirige eficientemente los recursos computacionales al estado límite que separa la falla y el éxito del diseño.
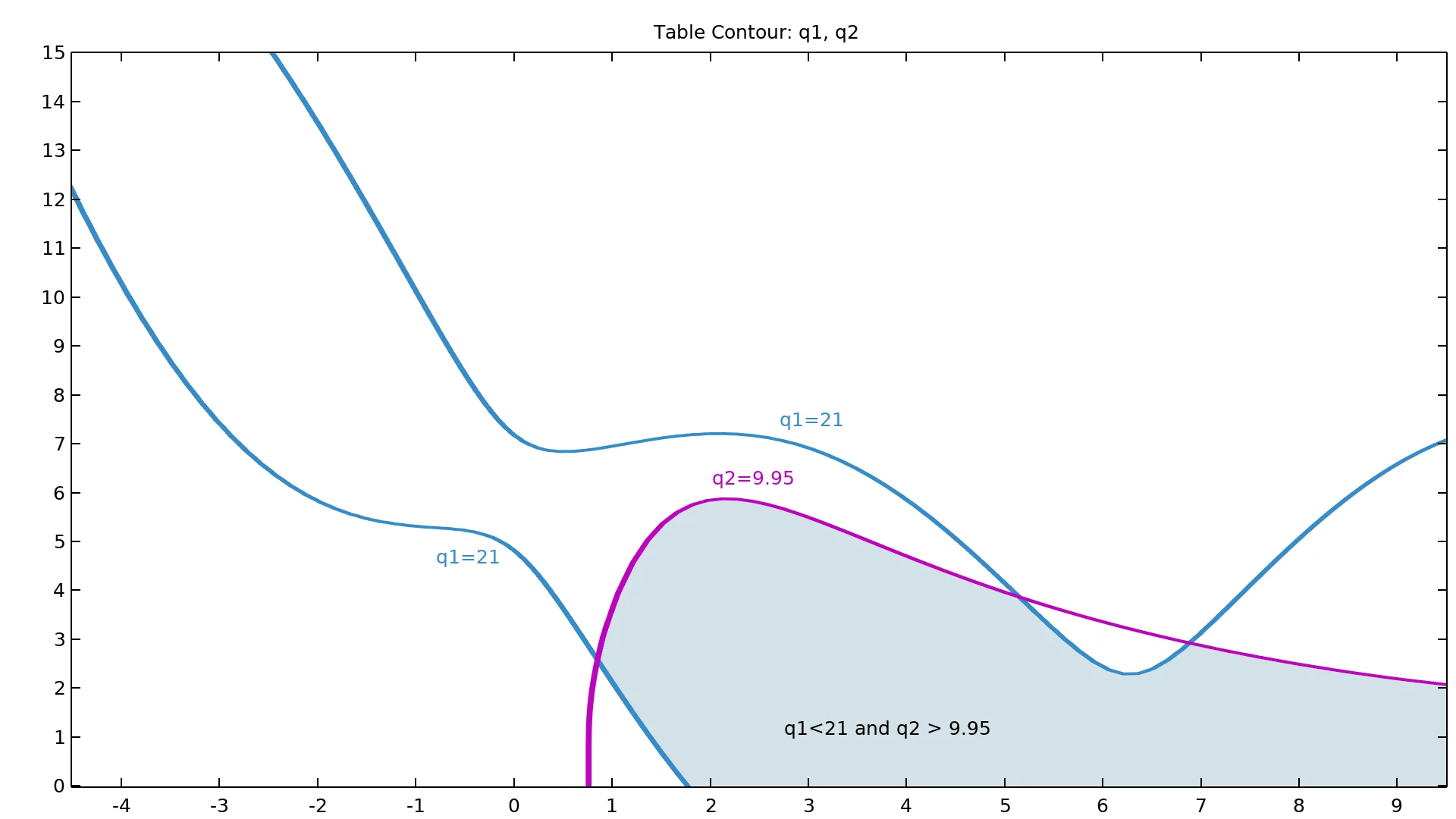
Líneas de contorno para los dos valores de interés q1 (azul) y q2 (morado) donde los niveles representan los umbrales q1 = 21 y q2 = 9.95 utilizados en el análisis de fiabilidad. Aquí se utilizan dos parámetros de entrada como ilustración (datos de eje x- e y-). La región sombreada muestra los parámetros de entrada que satisfacen el criterio de fiabilidad.
Modelos sustitutos y superficies de respuesta
Los análisis de sensibilidad calculados con el método Sobol, la propagación de la incertidumbre y el análisis de fiabilidad se basan en un análisis preciso tipo Monte Carlo. Esto a menudo requiere una gran cantidad de evaluaciones para lograr una buena precisión. Para problemas realistas en los que una evaluación del modelo de COMSOL Multiphysics® podría requerir recursos significativos y donde el análisis de cuantificación de la incertidumbre implica varios parámetros, un análisis de Monte Carlo realizado solo con evaluaciones del modelo COMSOL Multiphysics® no es factible computacionalmente. Una característica clave del Uncertainty Quantification Module es su capacidad para entrenar y utilizar un modelo sustituto, también conocido como metamodelo, para un análisis UQ particular para ahorrar recursos computacionales.
Un modelo sustituto es un modelo matemático compacto construido para representar y evaluar los valores de interés en el dominio de interés definido por los parámetros de entrada. Este modelo es completamente independiente del modelo COMSOL Multiphysics® subyacente y puede, cuando se entrena adecuadamente, usarse en lugar del modelo COMSOL Multiphysics® para predecir valores para las cantidades de interés para otros valores de los parámetros de entrada distintos a los resueltos. El proceso de construcción de un modelo sustituto suele ser adaptativo y el modelo sustituto puede aproximarse al modelo original con un alto grado de precisión. Las tolerancias definidas por el usuario le permiten aumentar la precisión de los modelos sustitutos. Un nivel más alto de precisión requiere evaluaciones adicionales de modelos de COMSOL Multiphysics®.
Una vez que se ha creado un modelo sustituto puede realizarse una verificación independiente para probar aún más su validez, y puede calcularse rápidamente los datos de la superficie de respuesta para todo el espacio de parámetros de entrada. A continuación, se puede visualizar una superficie de respuesta, donde se traza una cantidad de interés frente a dos parámetros de entrada a la vez.
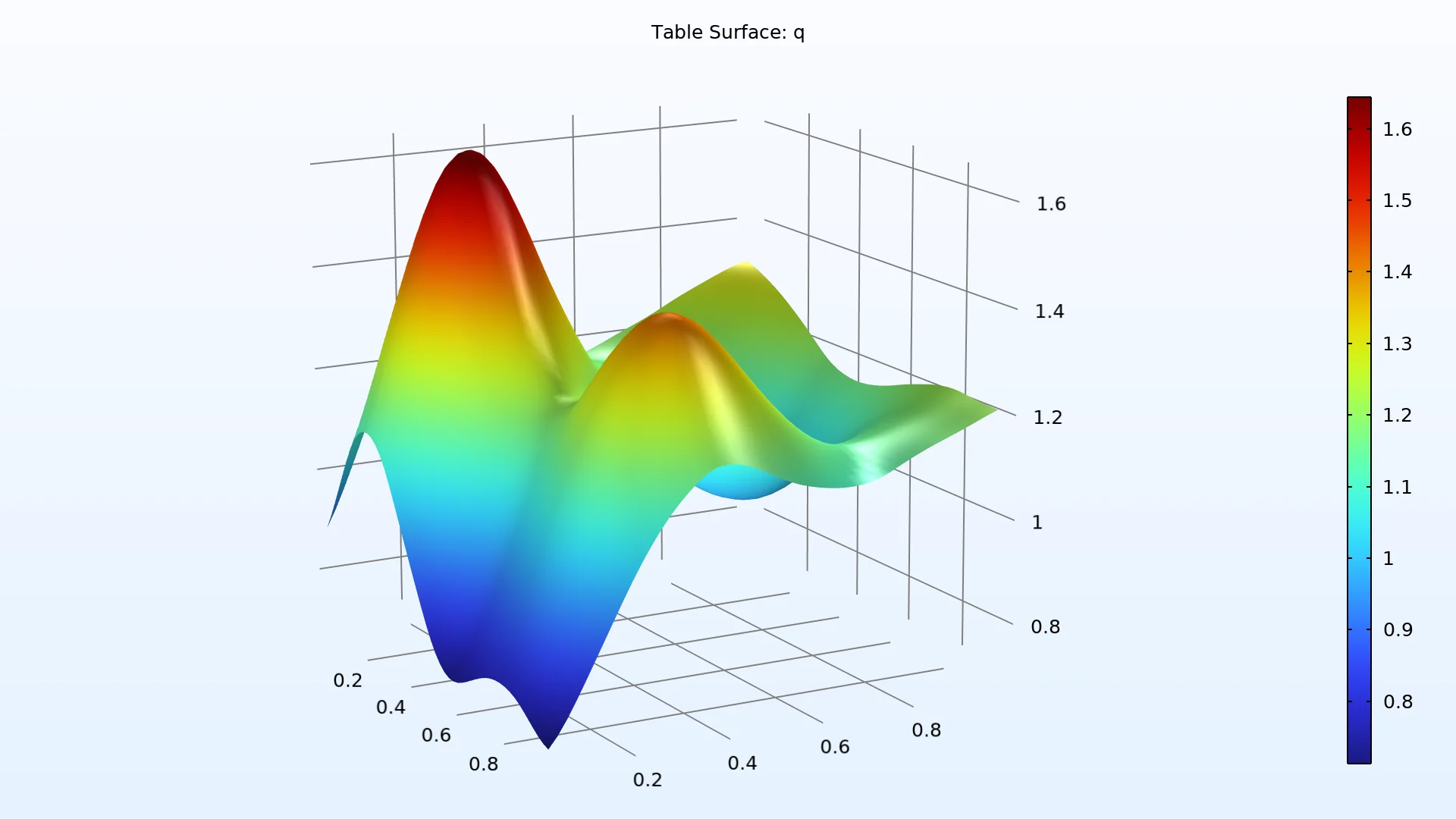
Un gráfico de superficie de respuesta de un valor de interés q como función de dos parámetros de entrada. Nótese que para problemas con más de dos parámetros de entrada, la superficie de respuesta puede actualizarse fácilmente por otro par de parámetros de entrada en los ajustes del gráfico.
VERSIONES
6.4
NOVEDADES
6.4 incorpora compatibilidad con magnitudes de interés (CdI) dependientes de la frecuencia y el tiempo, y permite definir la incertidumbre de medición para la cuantificación inversa de la incertidumbre (CU).
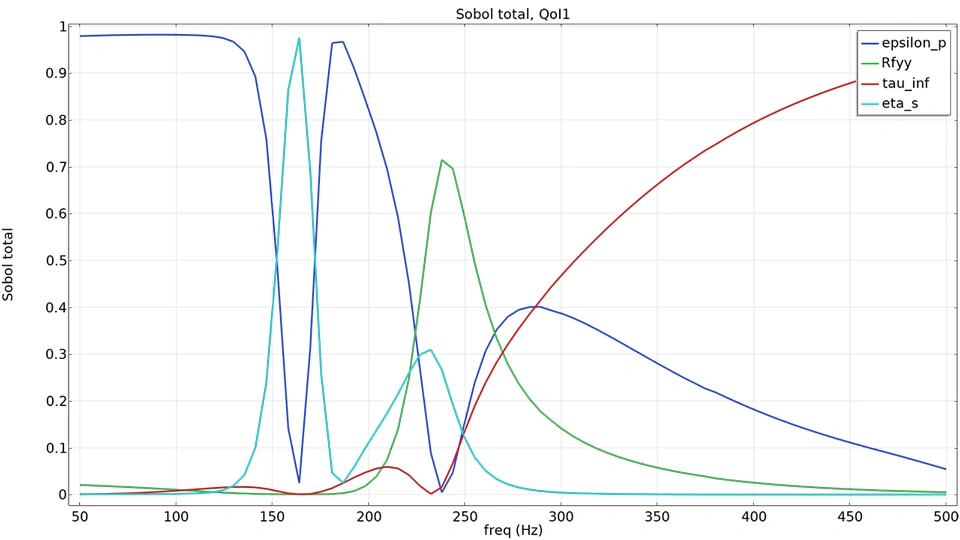
Cuantificación de la incertidumbre dependiente de la frecuencia y del tiempo
El Módulo de Cuantificación de Incertidumbre ahora admite QoI dependientes de la frecuencia y el tiempo, lo que permite un análisis UQ eficiente sin necesidad de realizar simulaciones adicionales. Todos los puntos de frecuencia o pasos de tiempo calculados del estudio subyacente se pueden utilizar directamente para realizar análisis de cribado, de sensibilidad, de propagación de incertidumbre y de fiabilidad. Esta mejora se aplica a cualquier modelo dependiente de la frecuencia o el tiempo y es especialmente útil en aplicaciones como RF, acústica, MEMS y simulaciones de baterías, donde el rendimiento suele depender de respuestas dependientes de la frecuencia y el tiempo. Ahora es posible explorar cómo se propaga la incertidumbre en los parámetros de entrada a lo largo de todo el espectro de frecuencia o tiempo. El modelo tutorial Piezoelectric Energy Harvester with Uncertainty Quantification demuestra esta nueva capacidad.
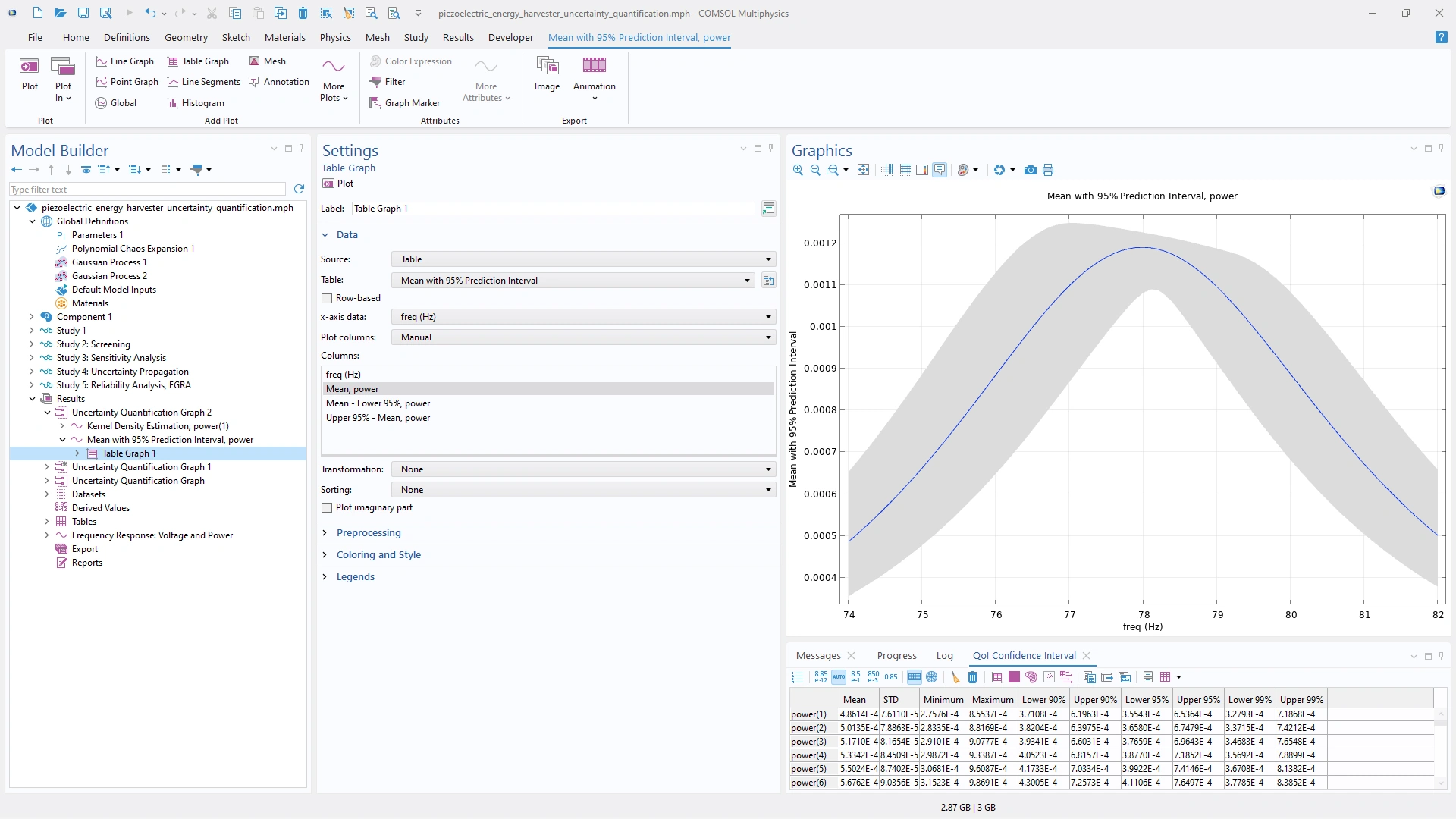
El estudio de cuantificación de incertidumbre ahora admite QoI dependientes de la frecuencia, lo que permite el análisis UQ de todas las expresiones de QoI que varían con la frecuencia.
Incertidumbre de medición definida por el usuario para UQ inversa
Los estudios de UQ inversa ahora admiten la incertidumbre de medición definida por el usuario, lo que ofrece mayor flexibilidad en la calibración de parámetros. Esta mejora permite definir explícitamente la incertidumbre de medición asociada a los datos experimentales. Cuando se conoce la incertidumbre de medición, incluirla en un estudio de UQ inversa permite una calibración más precisa de los parámetros de entrada. En los casos en que se desconoce la incertidumbre de medición, se puede estimar conjuntamente con los parámetros de entrada calibrados.
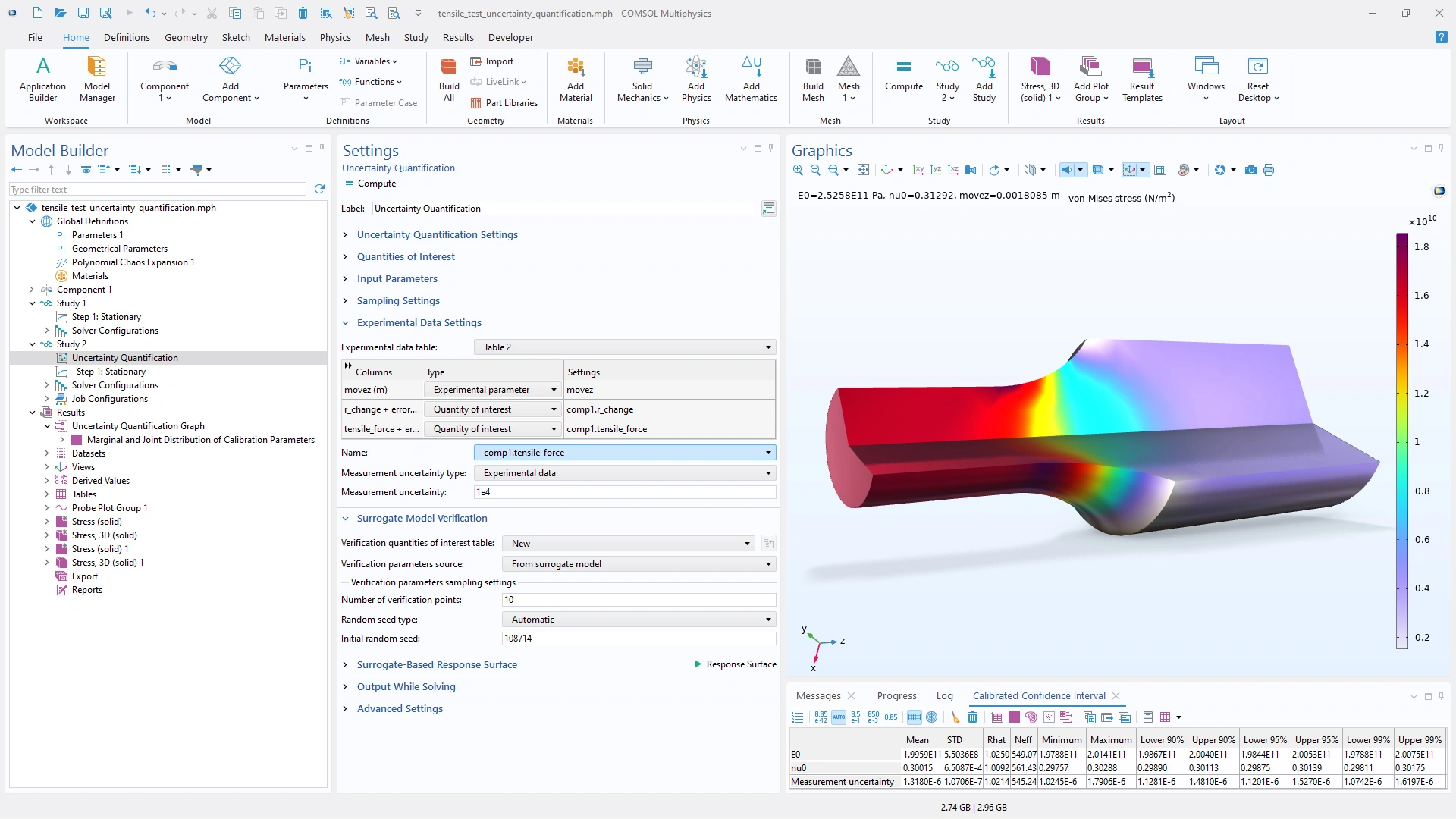
El estudio de cuantificación de incertidumbre ahora admite la incertidumbre de medición definida por el usuario a partir de configuraciones de datos experimentales para estudios de UQ inversa.
Nuevos modelos tutoriales
|
Piezoelectric Energy Harvester Uncertainty Quantification |
Uncertainty Quantification of Poroacoustic Parameters in a Transverse Isotropic Porous Material* |
|
Uncertainty Quantification of a Resistor |
6.2
NOVEDADES
Parámetros de entrada dependientes
Ahora puede definir parámetros de entrada correlacionados agrupándolos en grupos de correlación. Los puntos de datos se muestrean con el método de cópula gaussiana, que utiliza la matriz de correlación y distribuciones marginales para el muestreo de datos. Cuando se utilizan los ajustes de la función sustituta para especificar los parámetros de entrada y los parámetros de entrada de verificación del análisis de Monte Carlo, los mismos ajustes de correlación utilizados en el entrenamiento de la función sustituta se utilizan para muestrear datos para el análisis y la verificación de Monte Carlo. Estas operaciones amplían la funcionalidad de los estudios de cuantificación de la incertidumbre para respaldar mejor los parámetros de entrada multivariados.
Añadir función subrogada
Los tipos de estudios de cuantificación de la incertidumbre basados en sustitutos, incluido Sensitivity Analysis; Uncertainty Propagation; Reliability analysis, EGRA; y Inverse uncertainty quantification — ahora crea funciones subrogadas globales después de calcular el estudio. Luego, las funciones subrogadas se pueden evaluar con o sin el módulo de cuantificación de incertidumbre.
Gráficos de región de error
Además de utilizar el gráfico Error Bar disponible anteriormente, ahora también se puede visualizar las incertidumbres como una región coloreada dentro del gráfico. Esta nueva incorporación se puede utilizar para visualizar, por ejemplo, la incertidumbre en la regresión del proceso gaussiano. El nivel de incertidumbre mostrado también se puede personalizar para visualizar, por ejemplo, la región de 1 sigma, 2 sigma, etc.
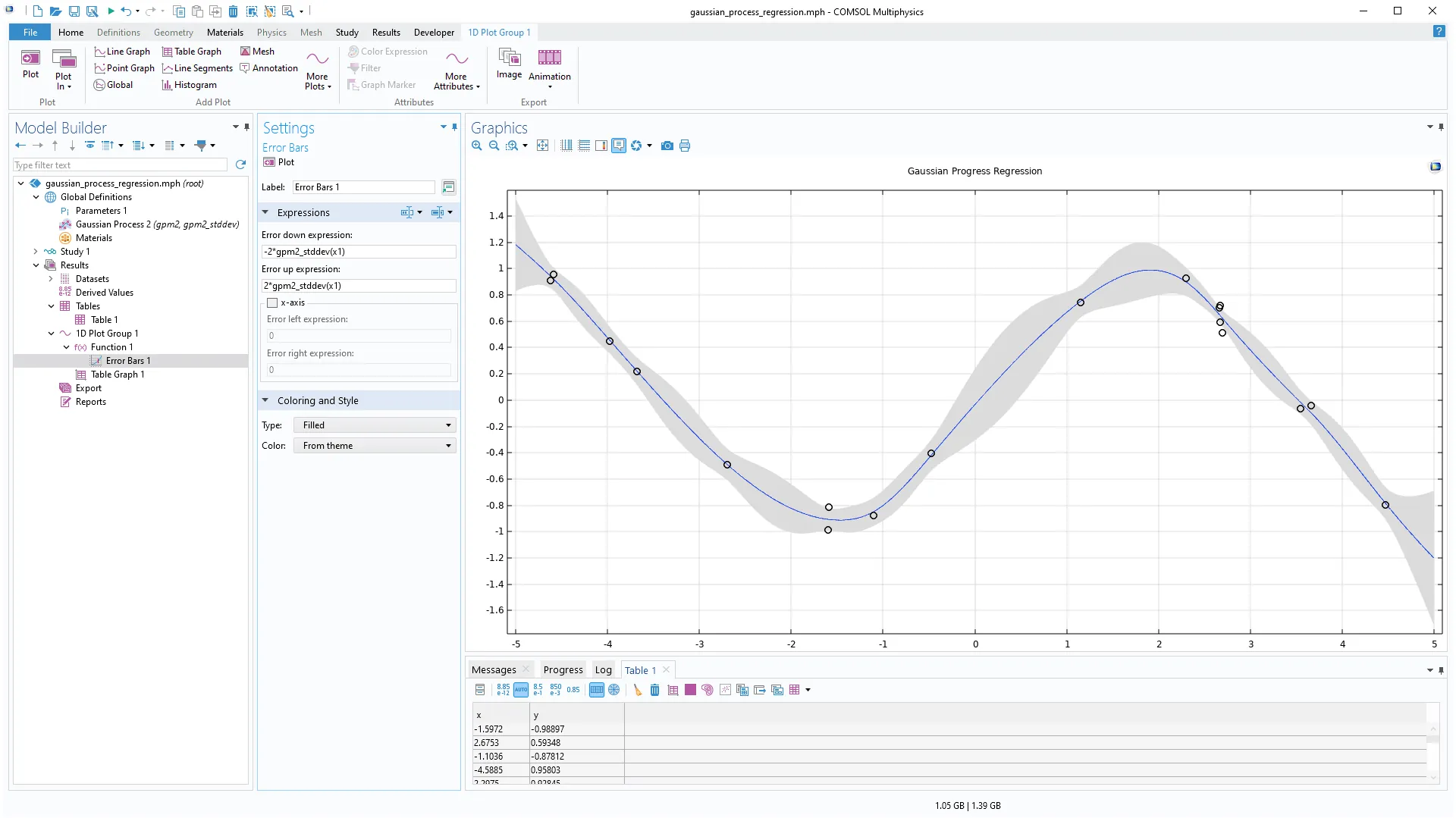
Un proceso de regresión gaussiano de datos ruidosos con una región de error que indica incertidumbre en el nivel 2 sigma.
Nuevos modelos tutoriales
|
Inverse Uncertainty Quantification for a Tensile Test |
Solidly Mounted Resonator 2D with Uncertainty Quantification |
6.1
NOVEDADES
La versión 6.1 presenta la capacidad de utilizar datos experimentales para calibrar la incertidumbre de entrada y nuevas formas de especificar parámetros de entrada.
Cuantificación inversa de la incertidumbre
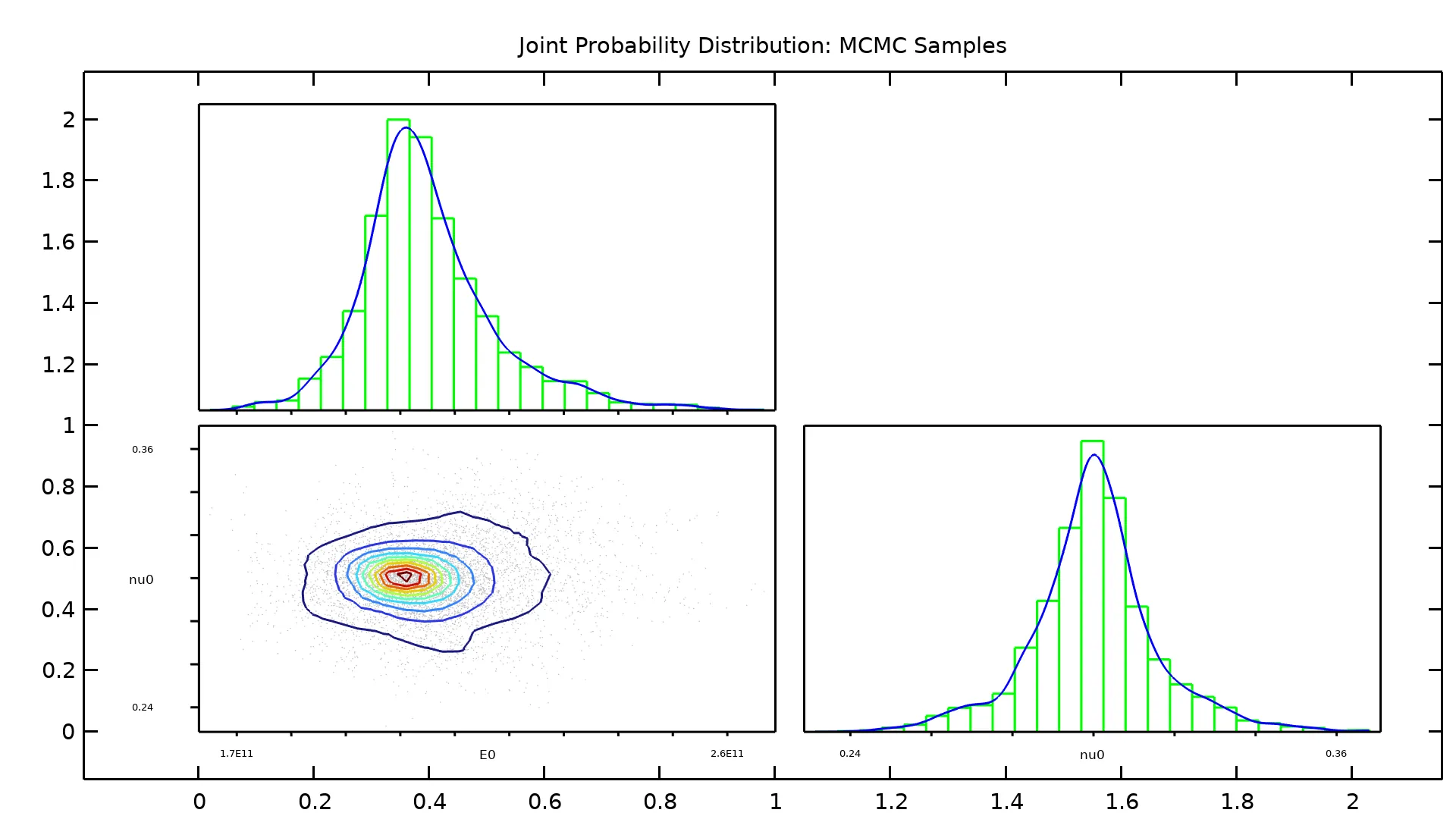
Ahora pueden utilizarse datos experimentales para calibrar las distribuciones de probabilidad desconocidas de los parámetros de entrada. El nuevo tipo de estudio Inverse Uncertainty Quantification se utiliza para calcular la distribución posterior de los parámetros de entrada, es decir, los parámetros de calibración que mejor reflejan su distribución en función de los datos experimentales y el conocimiento previo de los parámetros de calibración. El método Monte Carlo de cadena de Markov (MCMC) se utiliza para inferir la distribución posterior de los parámetros de calibración mediante la construcción de cadenas de Markov cuya distribución estacionaria es la distribución posterior. Este tipo de estudio propaga los datos experimentales hacia atrás para obtener conocimiento de los parámetros de calibración. Para obtener conocimiento de las cantidades de interés, se puede comparar este tipo de estudio con el tipo de estudio existente Uncertainty Propagation, que propaga la distribución de un parámetro conocido hacia adelante.
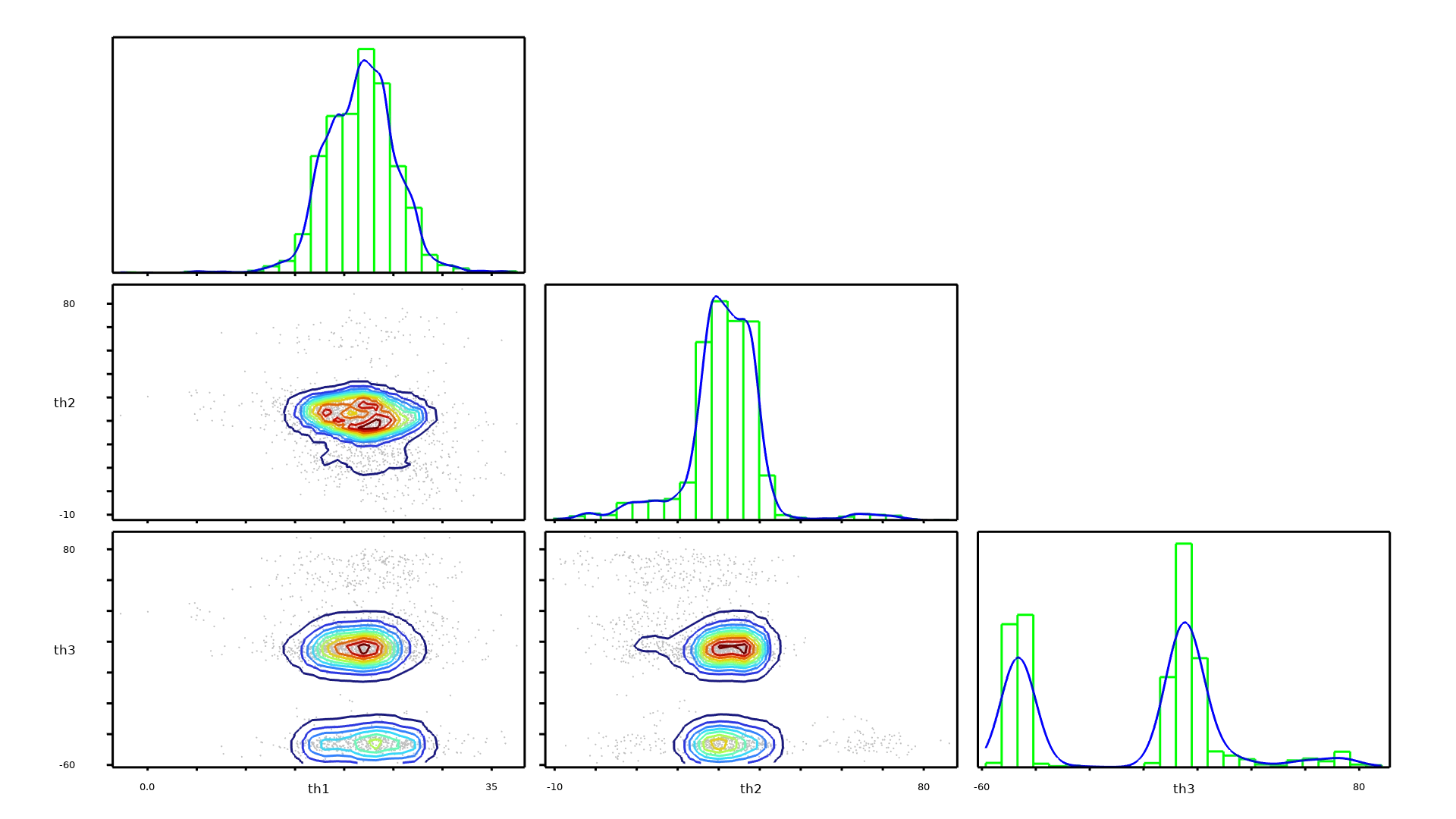
Un gráfico de distribución de probabilidad conjunta y distribución marginal, generado con muestras de MCMC. Los parámetros calibrados en el gráfico son las orientaciones de fibra de capas de secuencia de apilamiento en un laminado compuesto que coincide con las tensiones requeridas para una condición de carga específica.
Esquemas adicionales para parámetros de entrada
Hay nuevas formas de especificar los parámetros de entrada, los parámetros utilizados para el análisis Monte Carlo basado en sustitutos y los parámetros utilizados para la verificación del modelo sustituto. Los parámetros pueden tomar sus valores de distribuciones analíticas, columnas de datos de tablas de resultados o valores específicos.


 COMSOL Multiphysics 6.4
COMSOL Multiphysics 6.4