Por David Osborn

Dentro de muchos círculos de producción, particularmente en las industrias de proveedores y fabricación de automoción, el tamaño de la muestra estándar para estudios de capacidad es de 30 piezas o partes.

Como cualquier análisis estadístico, el tamaño de la muestra tiene un efecto inverso en el error. A medida que el tamaño de la muestra crece, el error decrece. A medida que se evalúa la capacidad de un proceso, se desea minimizar el error y por tanto posiblemente se querrá un tamaño de muestra más grande.

¿POR QUÉ SE REALIZA UN ESTUDIO DE CAPACIDAD DEL PROCESO? EXISTEN TRES RAZONES:

¿DE DÓNDE VIENE LA REGLA DEL 30?

Mucha gente utiliza 30 piezas como valor de corte por la idea errónea de que para que un análisis sea "estadísticamente significativo" se necesitan 30 muestras. Así que "30" se ha convertido en un número algo arbitrario que la gente tiende a acordar que es suficientemente grande. Mientras que es verdad que el número 30 tiene un papel en estadística, particularmente con la distribución-t, no existe relación entre el número y la capacidad de calcular de forma adecuada el comportamiento de un proceso y su capacidad de ajustarse a las especificaciones. Desgraciadamente, en esta aplicación, el número 30 es insuficiente para modelar apropiadamente el proceso.

EN LA INDUSTRIA DE AUTOMOCIÓN, EN REALIDAD ES UNA ¡REGLA DE 100!

Por ejemplo, en los manuales de control de procesos estadísticos (SPC) y proceso de aprovación de producción de piezas (PPAP) publicados por el Grupo de Acción de la Industria de Automoción (AIAG), se definen 100 piezas como el tamaño de muestra adecuado para un estudio inicial de capacidad (basado en 20 subgrupos de 5 o 25 subgrupos de 4). Sin embargo, cada proceso es diferente, así que el número "correcto" para cualquier proceso depende de sus fuentes de variación.

ENTONCES, ¿QUÉ ES? ¿30 PIEZAS? ¿100 PIEZAS? ¿MÁS O MENOS?

A diferencia del diseño de experimentos o los tests de hipótesis, los estudios de capacidad no tratan de la potencia estadística, sino de la variabilidad. ¿Se ha capturado todas (o la fuentes más grandes) de la variación del proceso en el estudio? Independientemente de cuántas muestras se toman, mediante el uso de Intervalos de confianza en el análisis de capacidad, se puede obtener un rango de dónde podría estar la verdadera capacidad. Si es muy grande podría ser un indicador de que la muestra era demasiado pequeña.

Ejemplo:

Supongamos que tenemos una población teórica (10000) de una distribución normal que tiene una media de 30mm y una desviación estándar de 1mm.

Con una especificación inferior (LSL) de 25mm y una especificación superior (USL) de 35mm, sabemos que la capacidad "verdadera" (utilizaremos Pp por simplicidad) es 1.67:

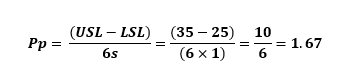
En Minitab, como se puede ver, utilizando toda la población, se obtiene una Pp de 1.67, que es exactamente la que se esperaba.

Ahora veremos la Pp que se obtiene cuando muestreamos esta población:

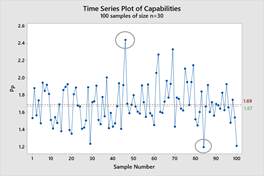
Escenario 1: Muestreamos esta población 100 veces con n=30

Ahora si muestreamos nuestros datos 100 veces utilizando muestras de 30 piezas, puede verse en el gráfico más abajo que se obtiene una gran variabilidad. En general, nuestro Pp promedio era de 1.69, que está cerca del valor "verdadero", pero nuestras muestras oscilaban en un rango entre un bajo 1.19 y un alto de 2.44. Efectivamente, obtenemos mucha variabilidad en los resultados de la muestra de 30 piezas, con Pp significativamente más bajos y más altos que el Pp de la población real. Utilizando solo este tamaño de muestra se podría llegar a una conclusión equivocada.

ENTONCES COMO NOS ASEGURAMOS QUE ESTAMOS ACERCÁNDONOS A LA Pp CORRECTA?

Una buena práctica para capturar la confiabilidad de la estimación de Pp es utilizar los Intervalos de confianza de Minitab, disponibles en Estadística>Herramientas de calidad>Análisis de capacidad>Normal>Opciones. Si muestreamos el proceso una vez, utilizando 30 piezas, y activamos los Intervalos de confianza, obtenemos los siguientes resultados:

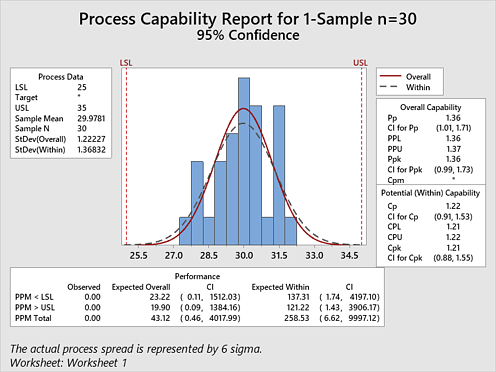
Como se puede ver, en base a la muestra única de 30 piezas, se obtiene uno de los valores bajos de Pp en 1.36, no muy cerca de la capacidad "verdadera" de la población, otra estimación poco fiable. Con solo mirar ese número se creería que el proceso no es capaz de 1.67.

Sin embargo, utilizando un intervalo de confianza de 95%, se puede ver dónde es probable que esté la capacidad "verdadera". Y un rango amplio como el que se tiene aquí tan bajo como 1.01 (no muy capaz según la mayoría de los estándares) o tan alto como 1.71 (muy capaz según la mayoría de estándares) es un indicador de que sencillamente no estamos seguros de qué es realmente capaz este proceso. Más muestras reducirán ese rango.

CONCLUSIÓN

En general, las muestras más grandes proporcionarán una mejor estimación de la verdadera capacidad. Los manuales AIAG SPC y PPAP recomiendan al menos 100 muestras. A veces obtener muestras puede ser difícil o costoso. De cualquier manera, utilizando los Intervalos de confianza de Minitab se obtendrá una mejor idea de la variabilidad y se evitarán errores costosos que pueden surgir como resultado de un tamaño de muestra pequeño.