Transferencia de calor por convección en COMSOL
- Detalles
- Categoría: Comsol
- Visto: 9189
Introducción
En el Webinar de Introducción a COMSOL Multiphysics hemos utilizado el modelo Busbar para mostrar cómo funciona el software y estudiar un caso multifísico. En aquel modelo, se somete una barra conductora de cobre (busbar) a una diferencia de potencial. Debido al efecto Joule, ésta se calienta. Adicionalmente, la barra sufre una deformación debido a la expansión térmica [1]. En esta ocasión miraremos con algo de detalle la incorporación del fenómeno de convección natural.
Coeficiente de transferencia de calor
En los fenónemos de Transferencia de Calor, el coeficiente de transferencia de calor es la constante de proporcionalidad entre el flujo de calor y la fuerza impulsora termodinámica para el flujo (es decir, la diferencia de temperatura, ΔΤ). Se utiliza para calcular la transferencia de calor, típicamente por convección o transición de fase entre un fluido y un sólido. El coeficiente de transferencia de calor tiene unidades SI de watios por metro cuadrado por Kelvin (W/m2/K).
Cuantitativamente, la tasa de transferencia de calor general para modos combinados generalmente se expresa en términos de una conductancia general o coeficiente de transferencia de calor. En ese caso, la tasa de transferencia de calor es (Ec. 1):
|
(1) |
La definición general del coeficiente de transferencia de calor es la ecuación siguiente, donde es el flujo de calor en W/m2 (Ec. 2).
|
(2) |
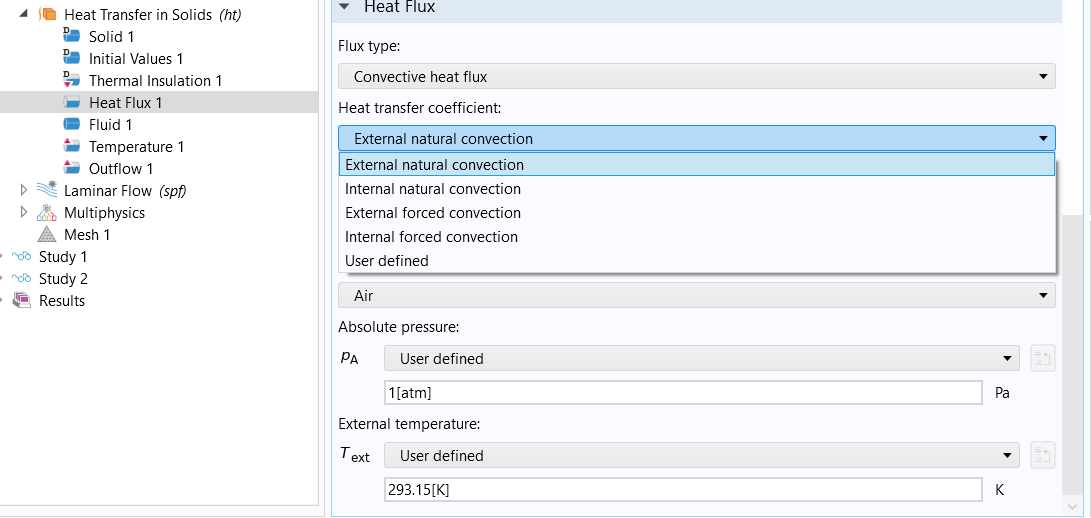
Aunque la transferencia de calor por convección se puede derivar analíticamente a través del análisis dimensional, el análisis exacto de la capa límite, el análisis integral aproximado de la capa límite y las analogías entre la transferencia de energía y cantidad de movimiento, es posible que estos enfoques analíticos no ofrezcan soluciones prácticas a todos los problemas cuando no existen métodos matemáticos. modelos aplicables. Por lo tanto, varios autores desarrollaron muchas correlaciones para estimar el coeficiente de transferencia de calor por convección en varios casos, incluida la convección natural, la convección forzada para el flujo interno y la convección forzada para el flujo externo [2]. Estas correlaciones empíricas se presentan para su particular geometría y condiciones de flujo. Como las propiedades del fluido dependen de la temperatura, se evalúan a la temperatura de la película. Dichos casos ya están implementados en COMSOL y se pueden escoger al implementar el nodo correspondiente (Fig. 1a) [3].
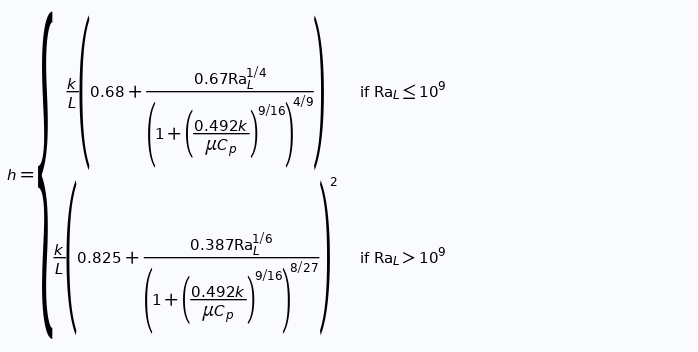
Las recomendaciones de Churchill y Chu proporcionan la siguiente correlación para la convección natural adyacente a un plano vertical, tanto para flujo laminar como turbulento [2]. En tales casos, k es la conductividad térmica del fluido, L es la longitud característica con respecto a la dirección de la gravedad, RaL es el número de Rayleigh con respecto a esta longitud. Se observa que se produce una transición de un límite laminar a uno turbulento cuando RaL excede alrededor de 109. (Fig. 1b).
|
|
|
|
Figura 1. Izquierda: Cada una de las opciones para definir convección (natural o forzada e interna o externa). Derecha: Ecuaciones para el caso de Convección Natural Externa. |
|
Hemos dicho que las expresiones empíricas, tanto para el caso de convección natural como también las existentes para la convección forzada, permiten abordar el fenómeno sin tener que implementar métodos analíticos imprácticos. No obstante, COMSOL Multiphysics se basa en el método de elementos finitos y podemos resolver problemas complejos numéricamente. Tal es el caso de si en lugar de utilizar el coeficiente de transferencia por convección podemos calcular la velocidad del fluido (aire) la cual participa de la ecuación del calor, a través del término (ρCpu·∇T) en la ecuación del calor. Para calcular u necesitamos de las ecuaciones de Navier Stokes [4].
Resultados
A continuación, se muestran resultados tras implementar la convección por medio del coeficiente de transferencia de calor y tras implementar CFD.
La Figura 3 muestra el resultado de la distribución de temperatura en todo el dispositivo cuando se le aplica una diferencia de potencial de 20 mV en sus terminales eléctricos y con un coeficiente de transferencia de calor de 5 W/(m2 K). En este caso, debido a que la convección está descrita por medio de la Ec. 1 y Ec. 2, no es posible detallar el transporte convectivo en el espacio que rodea al dispositivo.
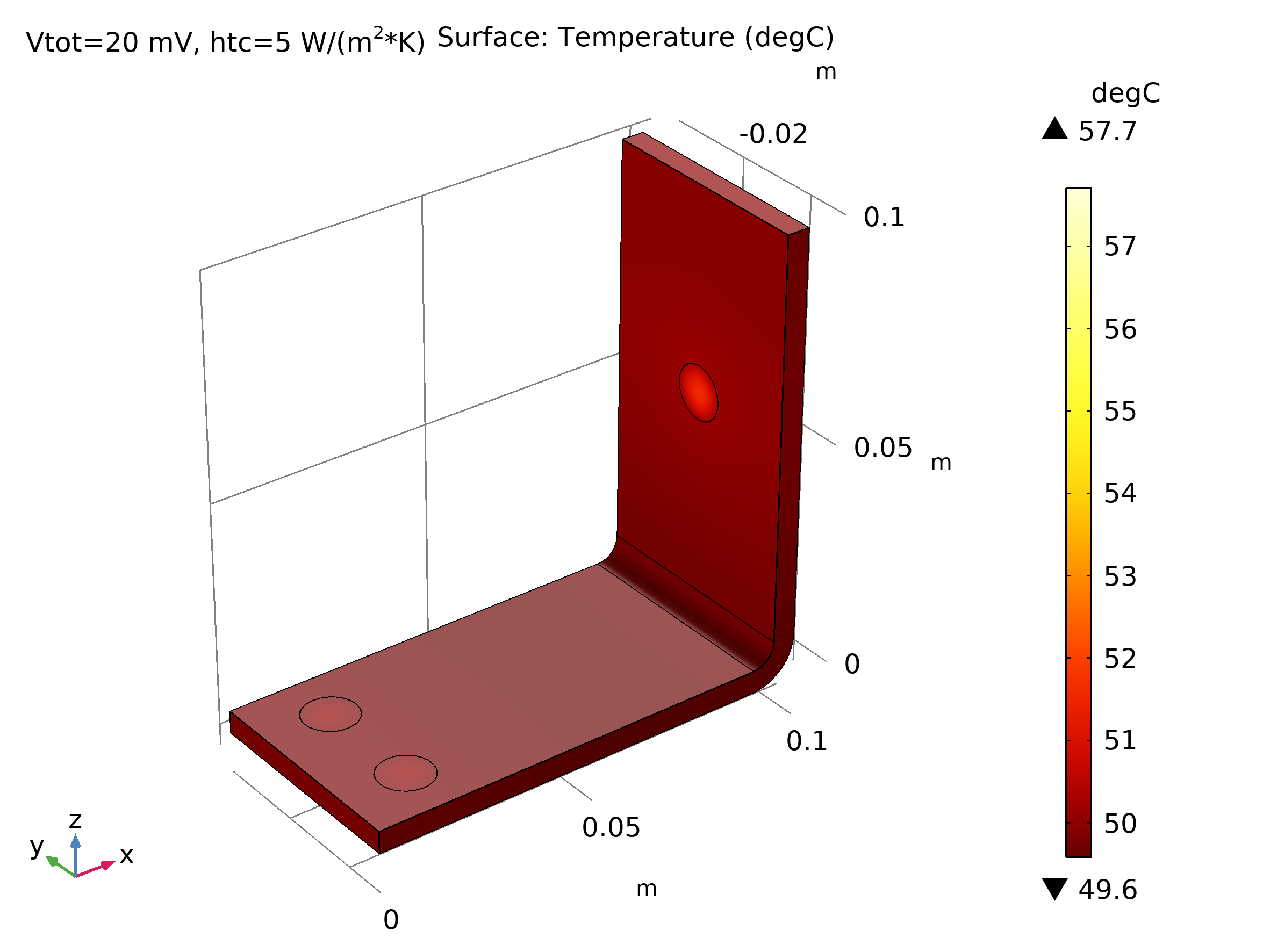
Figura 3: Distribución de la temperatura en la barra colectora, usando el coeficiente transferencia de calor para modelar la convección.
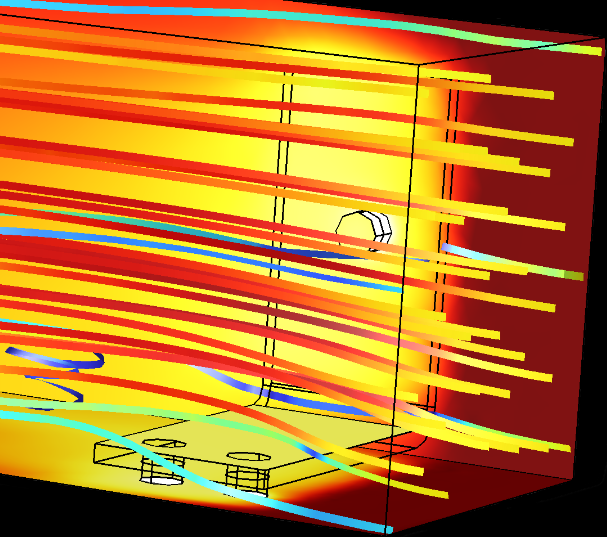
Por otra parte, la Figura 4 muestra el resultado de la distribución de temperatura en todo el dispositivo cuando se le aplica una diferencia de potencial de 20 mV en sus terminales eléctricos y con una velocidad de ingreso del aire de 0.1 m/s por el contorno del lado derecho. En este caso, no se utiliza un coeficiente de transferencia de calor (h), sino que la física de transferencia de calor se acopla a fluido dinámica. Así, es posible detallar el transporte convectivo en el espacio que rodea al dispositivo en donde se muestras streamlines para la velocidad del aire.
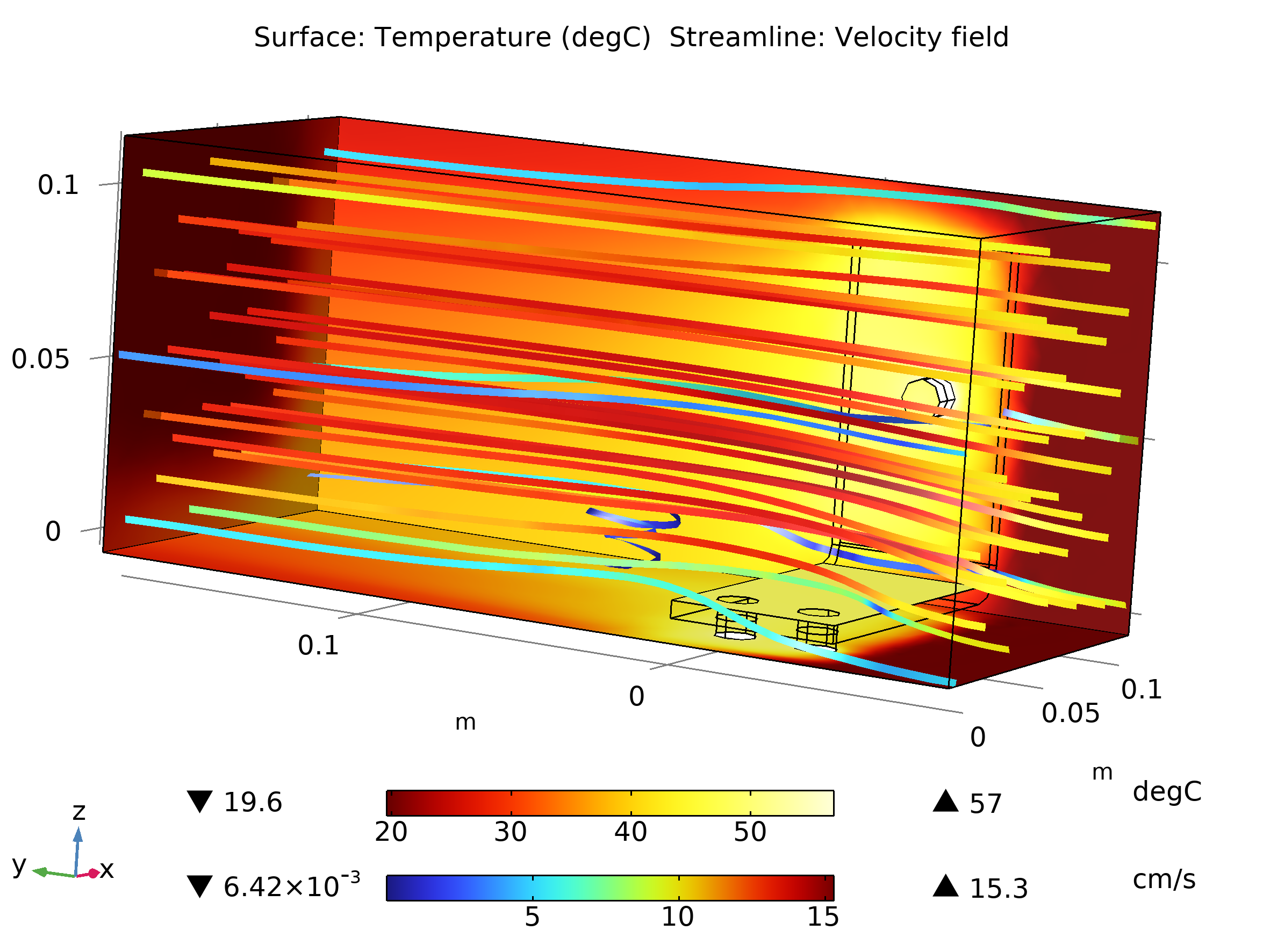
Figura 4: Distribución de la temperatura en el dispositivo (barra colectora) así como también en el dominio o región (bloque) donde se implementan las ecuaciones de Navier Stokes.
Referencias
[1] Vídeo "Introducción práctica a la simulación multifísica con COMSOL Multiphysics"
[2] Churchill, Stuart W.; Chu, Humbert H.S. (November 1975). "Correlating equations for laminar and turbulent free convection from a vertical plate". International Journal of Heat and Mass Transfer. 18 (11): 1323–1329.
[3] Heat Transfer Module User’s Guide
[4] https://www.comsol.com/multiphysics/navier-stokes-equations