Conozcamos el módulo Semiconductor Module de COMSOL Multiphysics
- Detalles
- Categoría: Comsol
- Visto: 5800
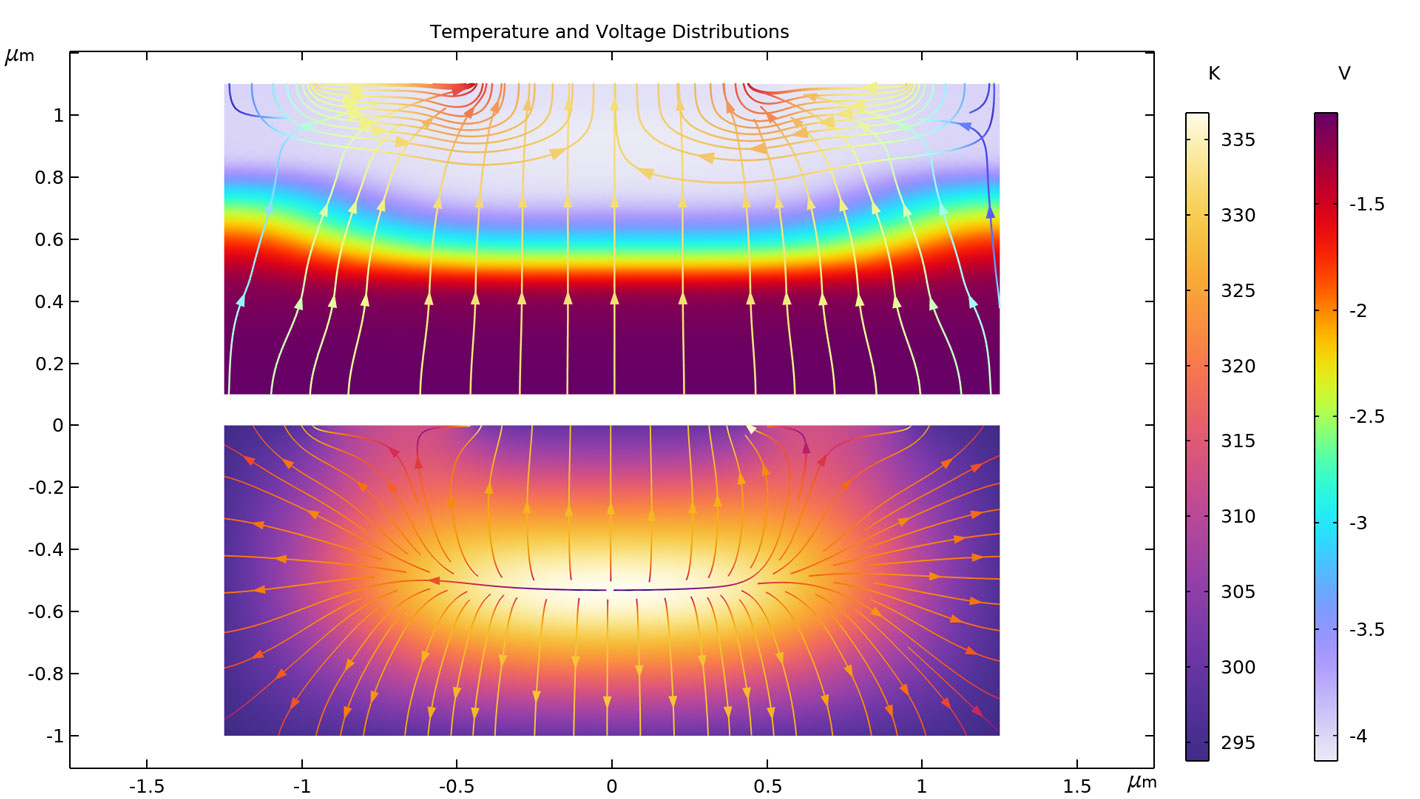
En la familia de productos de COMSOL Multiphysics, dentro del grupo de módulos sobre Electromagnetismo tenemos varios productos tales como AC/DC, RF, Wave Optics, Ray Optics, Plasma y Semiconductor. Dentro de ellas existen interfaces específicas para ciertos fenómenos de interés. Particularmente, el Semiconductor Module permite analizar el funcionamiento de dispositivos semiconductores al nivel físico fundamental. Las interfaces físicas dentro de él son las siguientes:
- Semiconductor (semi)
- Schrödinger Equation (schr)
- Schrödinger-Poisson Equation (schr)
- Semiconductor Optoelectronics, Beam Envelopes (ewbe)
- Semiconductor Optoelectronics, Frequency Domain (ewfd)
Una descripción sobre las ecuaciones que describen la física de cada interfaz se especifica a continuación.
Semiconductor Interface
La interfaz de Semiconductor da la posibilidad de describir a los electrones y huecos mediante la distribución de Maxwell-Boltzmann o Fermi-Dirac. Utiliza la Ecuación de Poisson para calcular el potencial eléctrico según la distribución de portadores de carga que existan. Los portadores de carga pueden ser electrones y huecos, así como también impurezas como donadores y aceptores. El transporte de los portadores, en términos de la densidad de corriente, se describe por medio del modelo de Drift-Diffusion (difusión-deriva), la cual tiene 3 términos principales: La respuesta de los portadores frente a i) un campo eléctrico, ii) un gradiente de concentración de portadores y iii) cambios de la temperatura. Bajo el nodo principal, se pueden incluir modelos de movilidad para electrones y huecos de tal modo de considerar las interacciones con la red cristalina L), impurezas (I), dispersión portador-portador (C), dispersión con impurezas neutras (N), saturación de velocidad en un campo intenso (E) y dispersión superficial (S). Como ejemplo, el modelo Arora toma en cuenta una combinación de estos procesos, siendo en modelo tipo LI.
Adicionalmente al sistema de ecuaciones, se añade una ecuación de continuidad debido a la recombinación de electrón-hueco y de la generación de pares electrón-hueco. La interfaz incluye los principales mecanismos de recombinación (Direct, Auger y Trap assisted recombination), y la posibilidad de definir una tasa de generación de pares electrón-hueco. Para extraer o inyectar portadores a un dispositivo se usan contactos metálicos. El contacto puede ser ideal óhmico o Schottky. Cuando se escoge Schottky, se pueden ingresar la Función de Trabajo (Metal Work Function), junto con los coeficientes de Richardson, e incluir un modelo para el tunelaje de electrones y huecos. Además, se pueden incluir velocidades de recombinación superficial (surface recombination velocities). Si, dentro del contacto Schottky se escoge User Defined, se puede ingresar la altura de la barrera (barrier height). Desde la versión 6.0 existe la posibilidad de activar el campo Contact Resistance (en la sección Terminal del nodo de Metal Contact). Con ello se puede especificar el valor de la resistencia específica de contacto (specific contact resistivity).
Desde el punto de vista numérico, se proporcionan dos métodos: el método del volumen finito y el método de elementos finitos estabilizado por mínimos cuadrados de Galerkin [1].
Schrödinger y Schrödinger-Poisson interfaces
Por un lado, la interfaz de la ecuación de Schrödinger resuelve la ecuación de Schrödinger para problemas generales de mecánica cuántica, así como para las funciones de onda de electrones y huecos en semiconductores cuánticos confinados bajo el supuesto de la aproximación de la función envolvente (envelope function).
Por otro lado, la interfaz multifísica de la ecuación de Schrödinger-Poisson combina la ecuación de Schrödinger y la electrostática (es) para modelar portadores de carga en sistemas cuánticos, también con confinamiento. El potencial eléctrico contribuye al término de energía potencial en la ecuación de Schrödinger. Una suma ponderada de las densidades de probabilidad de los eigenstates de la ecuación de Schrödinger contribuye a la densidad de carga espacial en la electrostática. Cuando se selecciona la interfaz de Schrödinger-Poisson, se añade la interfaz de Electrostatics (es) así como un nodo de multifísica para el acoplamiento.
Una descripción teórica de la física de esta interfaz junto con un ejemplo se encuentra disponible en el Blog de COMSOL [2]. Allí se muestra que la ecuación Schrödinger-Poisson permite simular potadores de cargas confinados en quantum wells, nanowires y dots. El ejemplo descrito se trata de un nanowire de GaAs para demostrar la utilización de la interfaz.
Semiconductor Optoelectronics, Beam Envelopes y Frequency Domain
En este caso, se combinan la interfaz Semiconductor con la interfaz Electromagnetic Waves, Beam Envelopes (ewbe) o Frequncy DOmain (ewfd). El acoplamiento se produce a través de la función Transiciones ópticas. Para ello, existe el nodo Optical Transitions el cual añade un término de generación de emisión estimulada (apropiado para materiales de banda prohibida directa) en los dominios de la interfaz Semiconductor. Este término es proporcional a la intensidad óptica en la interfaz “ewbe” o en la interfaz “ewfd”. Además, se tiene en cuenta la emisión espontánea (para materiales de banda prohibida directa). El efecto de la adsorción o emisión de luz se explica por un cambio correspondiente en la permitividad compleja o el índice de refracción en la interfaz de óptica ondulatoria. Estas interfaces se utilizan para modelar dispositivos como fotodiodos, diodos emisores de luz y diodos láser sin pozos cuánticos en materiales de banda prohibida directa. Un ejemplo práctico se encuentra disponible en [3], donde se modela y simula un fotodiodo PIN de GaAs. El estudio en el dominio de la frecuencia permite visualizar las características espectrales del dispositivo.
Observaciones finales
El módulo proporciona una interfaz fácil de usar para analizar y diseñar dispositivos semiconductores, simplificando en gran medida las tareas de simulación del dispositivo en la plataforma de COMSOL. Así, el módulo Semiconductor es útil para simular una gran variedad de dispositivos prácticos. La librería de modelos integrada contiene una suite de modelos diseñados para proporcionar instrucciones sencillas y demostrar cómo utilizar la interfaz para simular sus propios dispositivos. Semiconductor Module es particularmente adecuado para simular transistores incluyendo transistores bipolares, de efecto de campo metal-semiconductor (MESFET), efecto de campo metal-oxido-semiconductor (MOSFET), diodos Schottky, tiristores, uniones P-N y células solares. Dentro de la librería de aplicaciones, existen diversos ejemplos para simular dispositivos como transistores bipolares, transistores de efecto de campo metal-semiconductor (MESFET), transistores de efecto de campo metal-oxido-semiconductor (MOSFET), diodos Schottky, tiristores y uniones P-N. También existen aplicaciones como una célula solar acoplado con Ray Optics, donde se puede escoger la locación y considerar el recurso solar local [4]. Otro recurso disponible para aprender sobre este módulo se encuentra en el Webinar realizado por Addlink [5].
Referencias
[1] https://www.comsol.com/semiconductor-module
[2] https://www.comsol.com/blogs/self-consistent-schrodinger-poisson-results-for-a-nanowire-benchmark.
[3] https://www.comsol.com/model/gaas-pin-photodiode-19705
[4] https://www.comsol.com/model/si-solar-cell-with-ray-optics-36201
[5] https://www.addlink.es/eventos/comsol/webinar-taller-introduccion-practica-a-la-simulacion-de-dispositivos-semiconductores-con-comsol-multiphysics

