COMSOL Optimization Module 6.4
DESCRIPCIÓN
No importa la disciplina de ingeniería. Una vez que se tiene un modelo de un producto o un proceso, se desea mejorarlo. Optimization Module puede utilizarse en toda la familia de productos COMSOL Multiphysics. Se trata de una interfaz general para calcular soluciones óptimas a problemas de ingeniería. Cualquier entrada de un modelo, sean dimensiones geométricas, formas de piezas, propiedades de materiales, o distribución de materiales, puede ser tratada como variable de diseño, y cualquier salida del modelo puede ser una función objetivo.
Optimization Module calcula las sensibilidades analíticas de la función objetivo para las variables de diseño, considera cualquier restricción impuesta al problema, y utiliza una técnica de optimización basada en el gradiente para encontrar los diseños óptimos. Se basa en el código SNOPT desarrollado por Philip E. Gill de la Universidad de California San Diego, y Walter Murray y Michael A. Saunders de la Universidad de Stanford. El módulo de Optimización puede utilizarse para resolver problemas de optimización de formas, tamaños y topología, así como problemas inversos como estimación de parámetros.
VERSIONES
6.4
NOVEDADES
6.4 introduce condiciones de parada para la optimización dependiente del tiempo, un paso de estudio de Optimización de Parámetros y varios modelos tutoriales nuevos
Optimización dependiente del tiempo
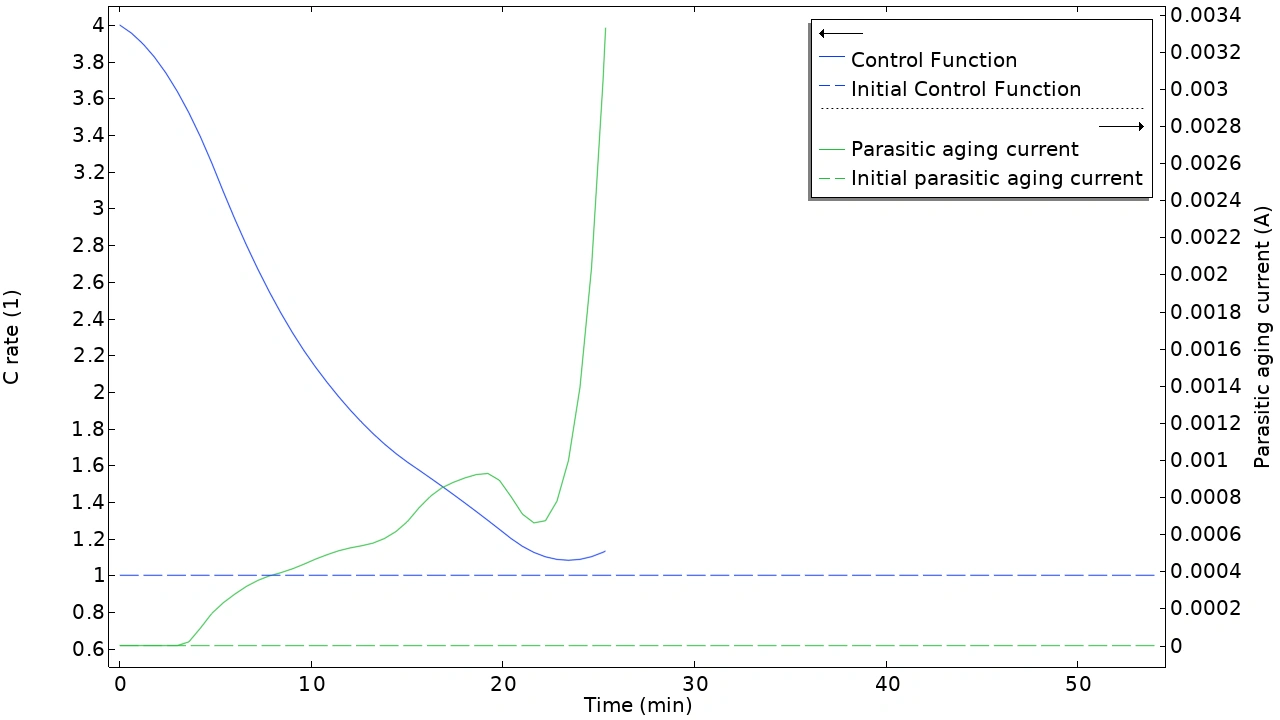
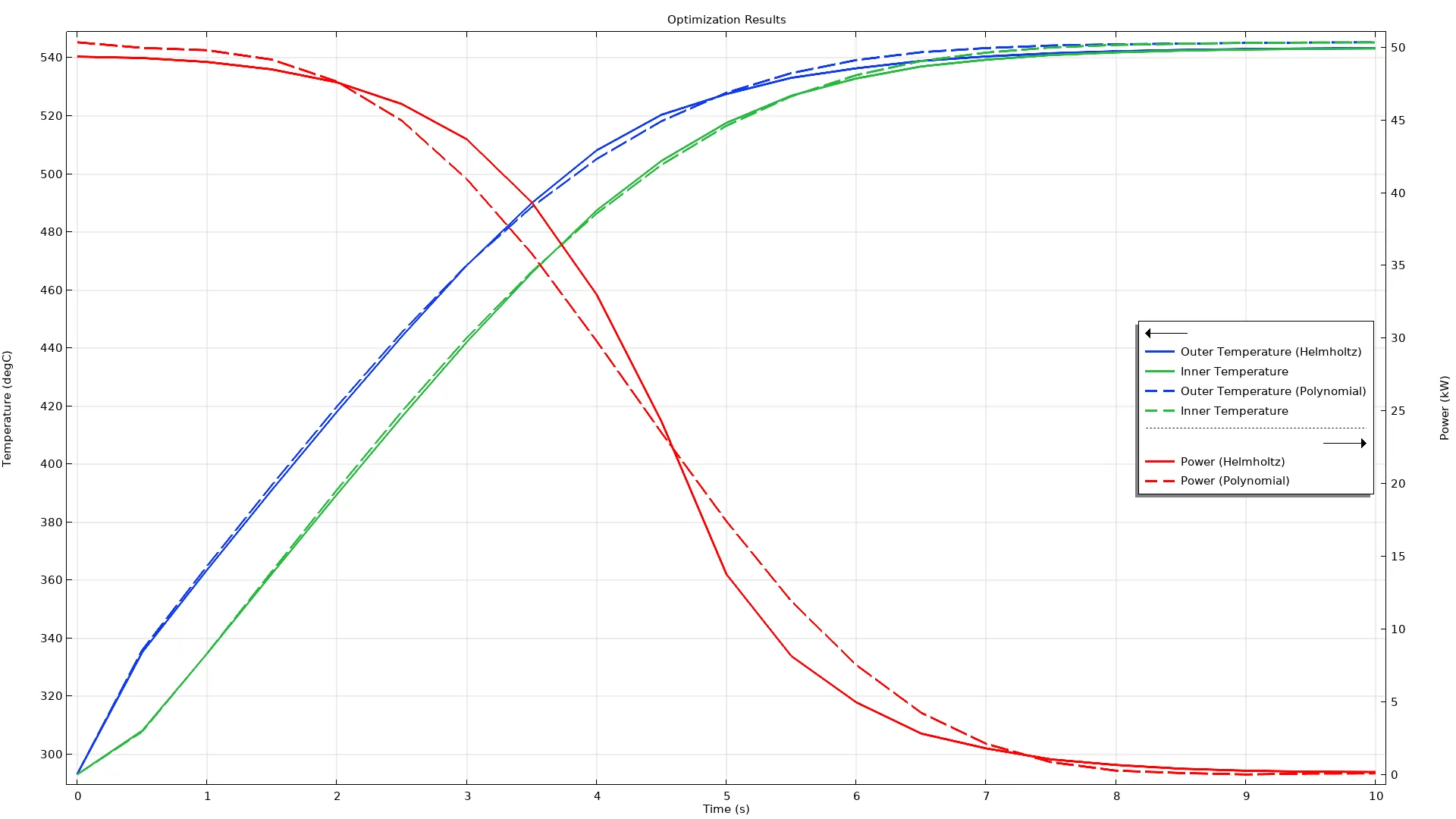
La optimización basada en gradientes para problemas dependientes del tiempo ahora también permite optimizar el tiempo final. Esto significa que es posible minimizar la duración de un proceso o dejar que el solucionador elija el tiempo que proporcione el mejor valor objetivo. En el ejemplo siguiente, el objetivo es minimizar el tiempo de carga de una batería de iones de litio. El modelo utiliza la función Control Function, que ahora permite exportar el resultado optimizado como función analítica o de interpolación.
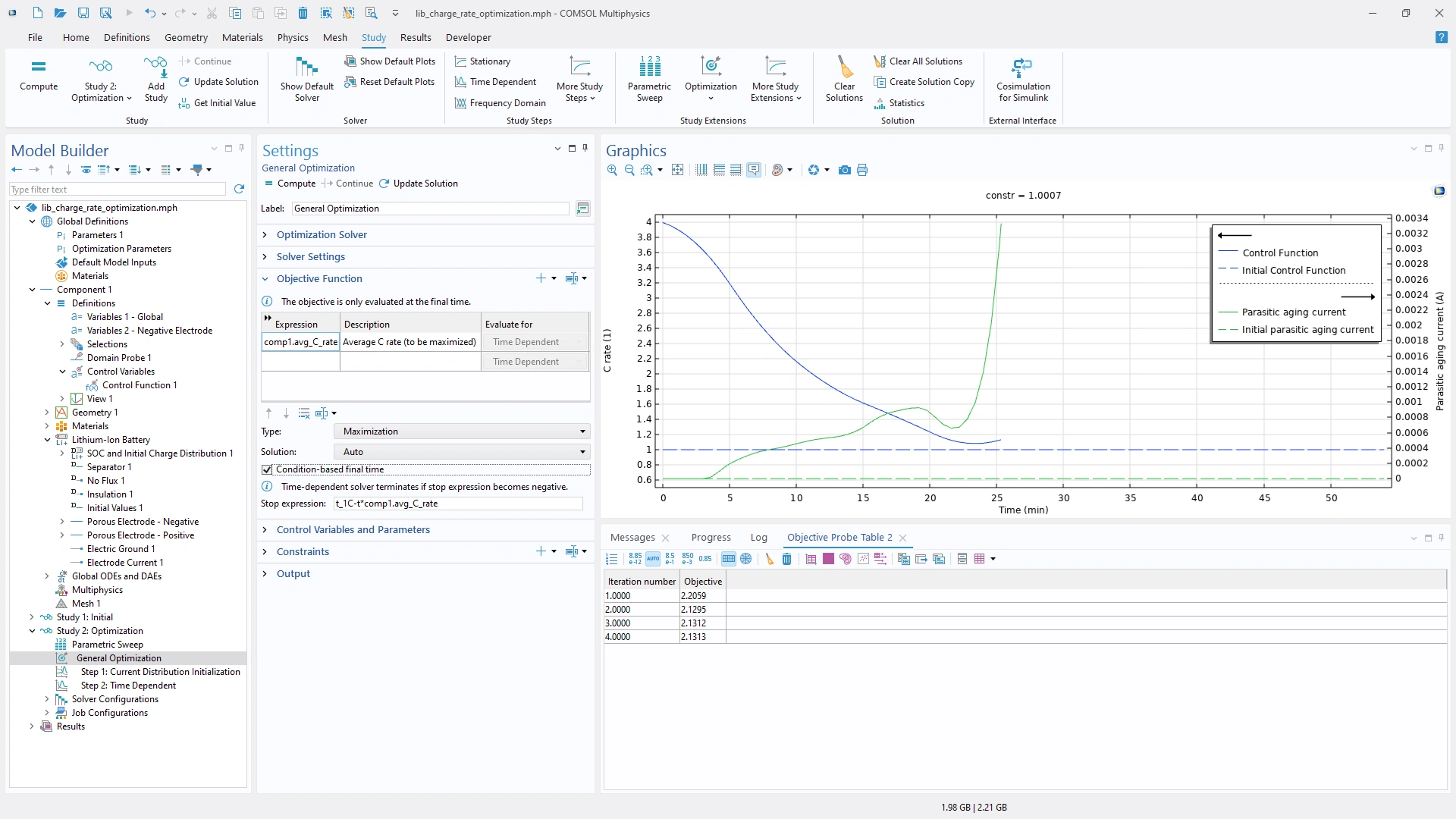
La casilla de verificación "Tiempo final basado en condición" se muestra en la configuración del paso del estudio de Optimización General . Este ejemplo optimiza el perfil de carga de una batería de iones de litio con una restricción en la degradación. El modelo muestra cómo la función de control ahora crea una variable para su valor promedio.
Optimización de parámetros
Se ha introducido un paso de estudio de Parameter Optimization, diseñado específicamente para la optimización sin gradiente, donde las escalas de control se establecen en función de los límites, eliminando así la necesidad de definirlas manualmente. Esta función también permite la creación automática de nuevos casos de parámetros basados en los parámetros optimizados.
Además, la interfaz de usuario se ha reorganizado en relación con el antiguo paso de estudio Optimization, que ahora se denomina General Optimization. Tanto el paso de estudio General Optimization como el de Parameter Optimizatin permiten la aleatorización de los valores iniciales de los controles globales acotados, lo que permite identificar diferentes mínimos locales.
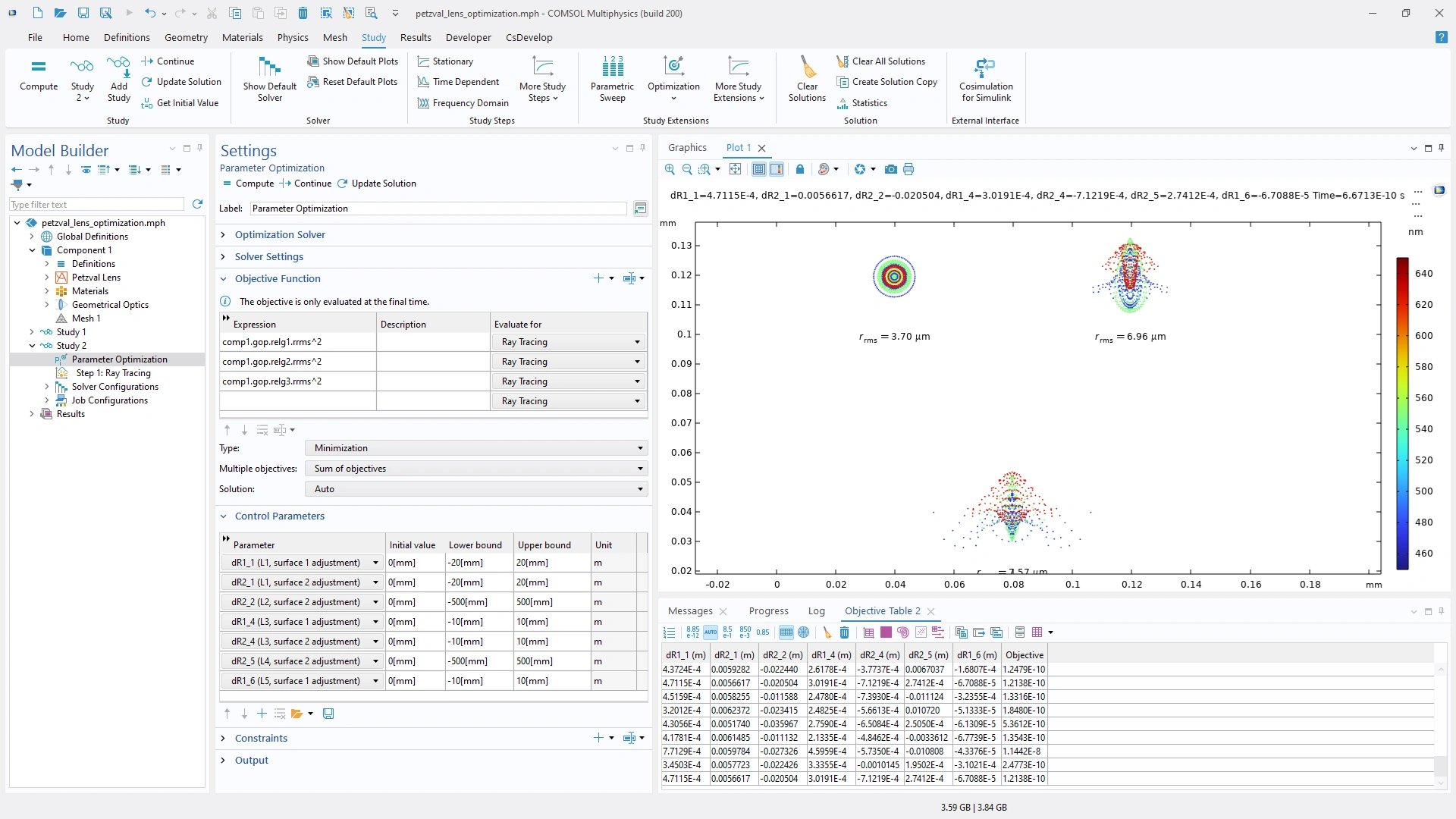
Este ejemplo demuestra un análisis de óptica de rayos que implica la optimización de un sistema de lentes para diferentes colores y ángulos de campo.
Resolvedores de optimización basados en gradientes
El resolvedor de optimización SNOPT se ha descontinuado; los modelos antiguos se han migrado a IPOPT, que ahora es el método recomendado para lograr la convergencia cuadrática (excepto para la estimación de parámetros, donde se espera que el resolvedor Levenberg-Marquardt sea superior). Además, al elegir la opción MMA en un paso de estudio de optimización, se activaba el uso de GCMMA (para la configuración predeterminada del resolvedor); sin embargo, ahora tanto MMA como GCMMA están disponibles a nivel de estudio.
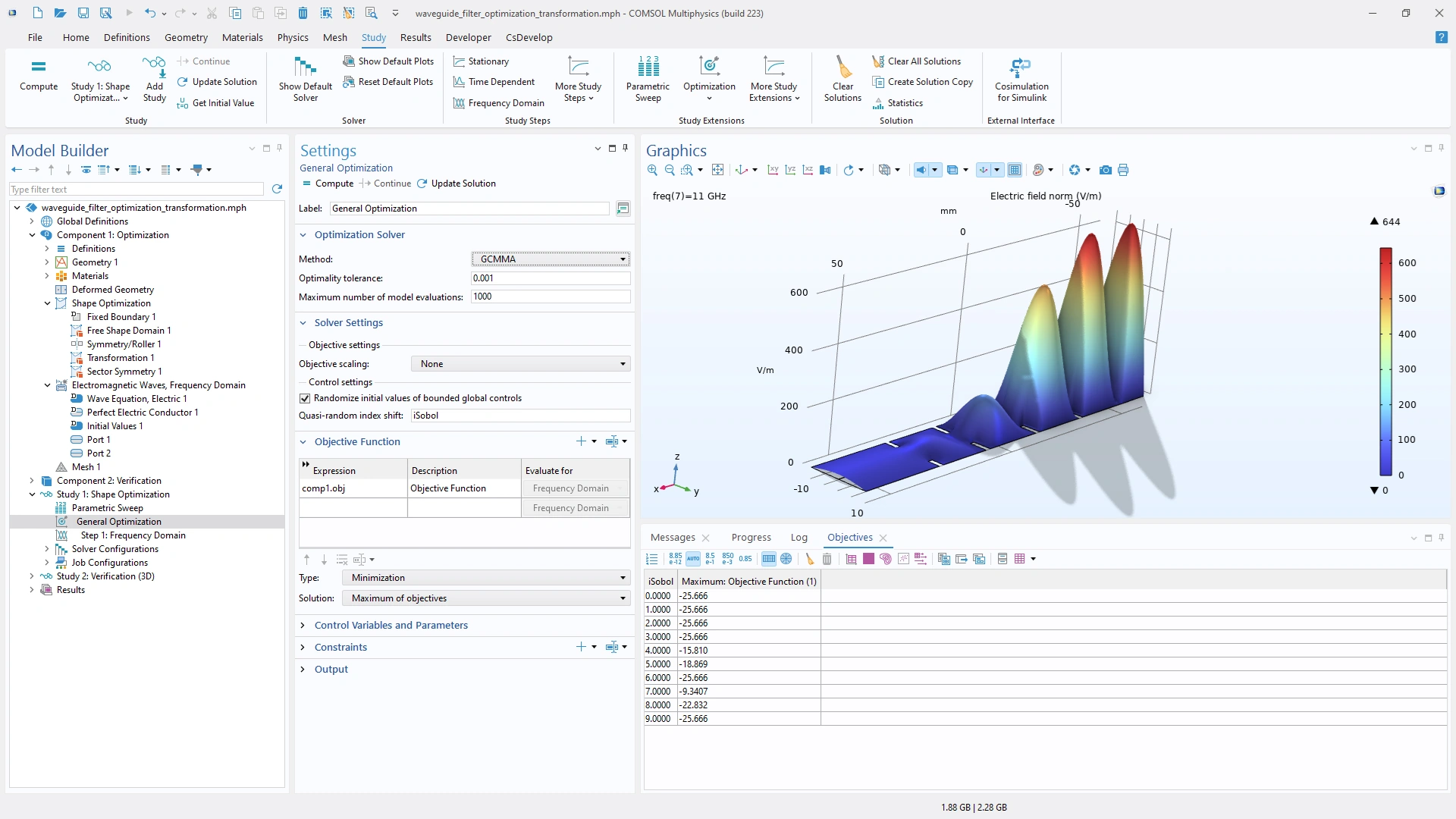
Los métodos de optimización GCMMA y MMA ya están disponibles para los pasos del estudio de optimización, como se demuestra en este modelo de ejemplo, donde se utiliza la optimización de forma en el diseño de un filtro de RF. El modelo también muestra cómo aleatorizar los controles iniciales para identificar diferentes óptimos locales.
Nuevas funciones y mejoras diversas
- Nuevas funciones P-norm y Standard Deviation:
- La función P-norm puede aproximar el valor máximo de un campo de una manera que sea compatible con la optimización basada en gradientes, como se usa a menudo para restricciones de tensión en problemas estructurales.
- La función Standard Deviation se puede utilizar para homogeneizar un campo en una selección.
- Se han añadido operadores de campo lejano compatibles con la optimización basada en gradientes a la interfaz Electromagnetic Waves.
- La optimización de valores propios ahora admite el uso de operadores no analíticos en la expresión objetivo, de modo que es posible diseñar para una frecuencia propia objetivo considerando solo la parte real.
- Se ha agregado soporte para restricciones de extrusión a la función Density Model.
- Se han realizado mejoras de rendimiento para la optimización basada en gradientes.
Nuevos modelos tutoriales
|
Time-Optimal Control for Heating of a Rod |
Designing a Metasurface Beam Deflector Using Shape Optimization |
|
Minimizing the Charging Time of a Lithium-Ion Battery |
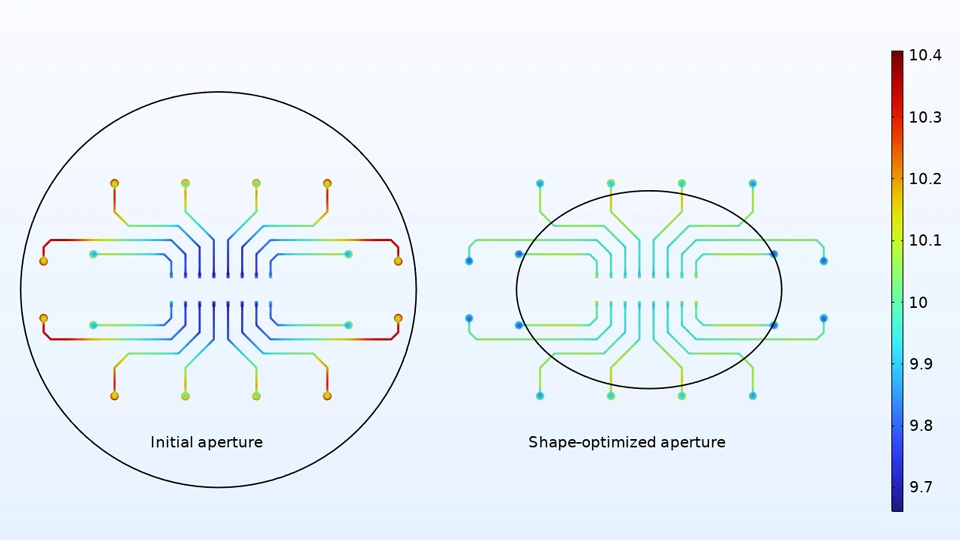
Aperture Shape Optimization for Electroplating of a Printed Circuit Board |
|
Wheel Rim — Stress Optimization with Fatigue Evaluation |
Topology Optimization of a Metalens |
|
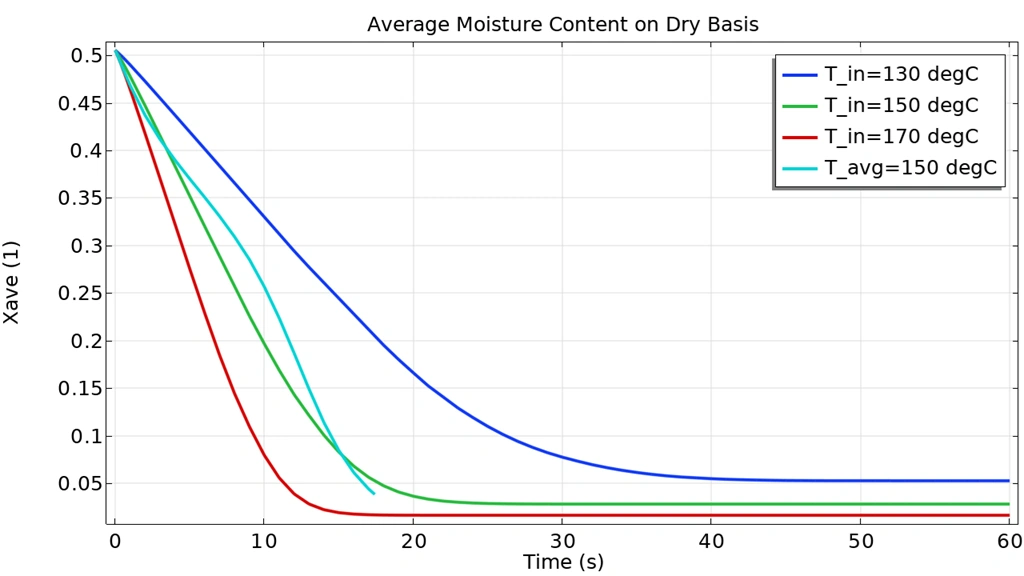
Minimizing the Drying Time of a Wood Particle |
6.3
NOVEDADES
La versión 6.3 ofrece una mayor solidez y velocidad para la optimización dependiente del tiempo, un nuevo resolvedor de optimización global eficiente (EGO) y varios modelos tutoriales nuevos.
Optimización dependiente del tiempo
El algoritmo para la optimización basada en gradientes de problemas dependientes del tiempo se ha mejorado para utilizar el método adjunto discreto. Esto funciona de manera similar a cómo se realizan todos los cálculos de gradientes estacionarios en el software COMSOL ® . Si bien el algoritmo adjunto continuo anterior aún está disponible, este método adjunto discreto es más robusto, tiene mejor precisión y es más rápido. Tenga en cuenta que ambos algoritmos pueden requerir un recálculo de la solución hacia adelante, pero la robustez de estos cálculos reiniciados se ha mejorado significativamente. Además, el nuevo método proporciona una aceleración igual al número de puntos de medición en el tiempo cuando se utiliza para la estimación de parámetros con el resolvedor de optimización del optimizador de puntos interiores (IPOPT) o el optimizador no lineal disperso (SNOPT).
Se puede acceder a las configuraciones avanzadas para la optimización basada en gradientes de problemas dependientes del tiempo seleccionando Adjoint como el método de gradiente para el Optimization Solver. Las configuraciones predeterminadas son sólidas, por lo que los ajustes suelen ser innecesarios y ofrecen pocos beneficios adicionales.
Optimización global eficiente
El resolvedor de optimización global eficiente (EGO) se ha añadido como un nuevo resolvedor de optimización sin gradiente al paso de estudio Optimization. Este resolvedor utiliza la optimización bayesiana para construir un modelo subrogado que enfatiza la precisión en áreas con buenos objetivos. Los resolvedores locales de versiones anteriores (como el resolvedor de optimización de límites por aproximación cuadrática [BOBYQA]) son más rápidos que este resolvedor; sin embargo, en algunos casos, el resolvedor EGO identifica de manera consistente mejores valores objetivos. El resolvedor EGO requiere límites en el parámetro de control, pero no se utilizan valores iniciales ni escalas. Es posible inspeccionar la superficie de respuesta gaussiana después de la optimización, lo que puede ser útil para evaluar la sensibilidad del objetivo a las perturbaciones en diferentes regiones. El resolvedor comparte funcionalidad y configuración con el módulo Uncertainty Quantification Module, pero solo requiere una licencia para el módulo Optimization Module.

El resolvedor EGO está disponible para el paso de estudio Optimization. Aumentar la cantidad de muestras iniciales por variable de control puede mejorar la probabilidad de identificar el óptimo global. El resultado se puede mejorar aún más cambiando a otro resolvedor sin gradiente (local) y continuando la optimización utilizando el botón Continue en la ventana Settings.
Optimización de valores propios
En la versión 6.3, se ha añadido compatibilidad con problemas de valores propios no lineales y es compatible con las funciones existentes para la optimización de valores propios, incluido el paso de estudio Stationary Then Eigenfrequency. También hay nuevas herramientas para ordenar y filtrar los valores propios, que pueden resultar útiles en el contexto de la optimización.

Las configuraciones para ordenar y filtrar soluciones de valores propios están disponibles para varios pasos de estudio, incluido el paso de estudio Stationary Then Eigenfrequency.
Tipo de resolvedor adjunto discreto
Hay disponible un nuevo tipo de resolvedor adjunto Time discrete para el control óptimo y la estimación de parámetros dependientes del tiempo. Este tipo de resolvedor se basa en un método de sensibilidad discreta, que proporciona mayor solidez, mayor precisión y un rendimiento más rápido para la optimización basada en gradientes con el Time-Dependent Solver.
En los problemas de estimación de parámetros transitorios, se logran mejoras de velocidad significativas con los solucionadores SNOPT o IPOPT. Esta aceleración se debe a que la sensibilidad agregada de todo el objetivo se calcula en una sola pasada en lugar de realizar cálculos separados para cada punto de medición. El método de sensibilidad continua anterior aún está disponible, pero ya no es el predeterminado para la optimización transitoria.
Tanto los métodos discretos como los continuos reducen el consumo de memoria mediante la creación de puntos de control, lo que implica el recálculo de la solución de avance. Además, existe una nueva opción Out-of-core que se puede utilizar de forma alternativa para el manejo de la solución de avance, que en su lugar utiliza espacio de disco temporal para evitar el recálculo.
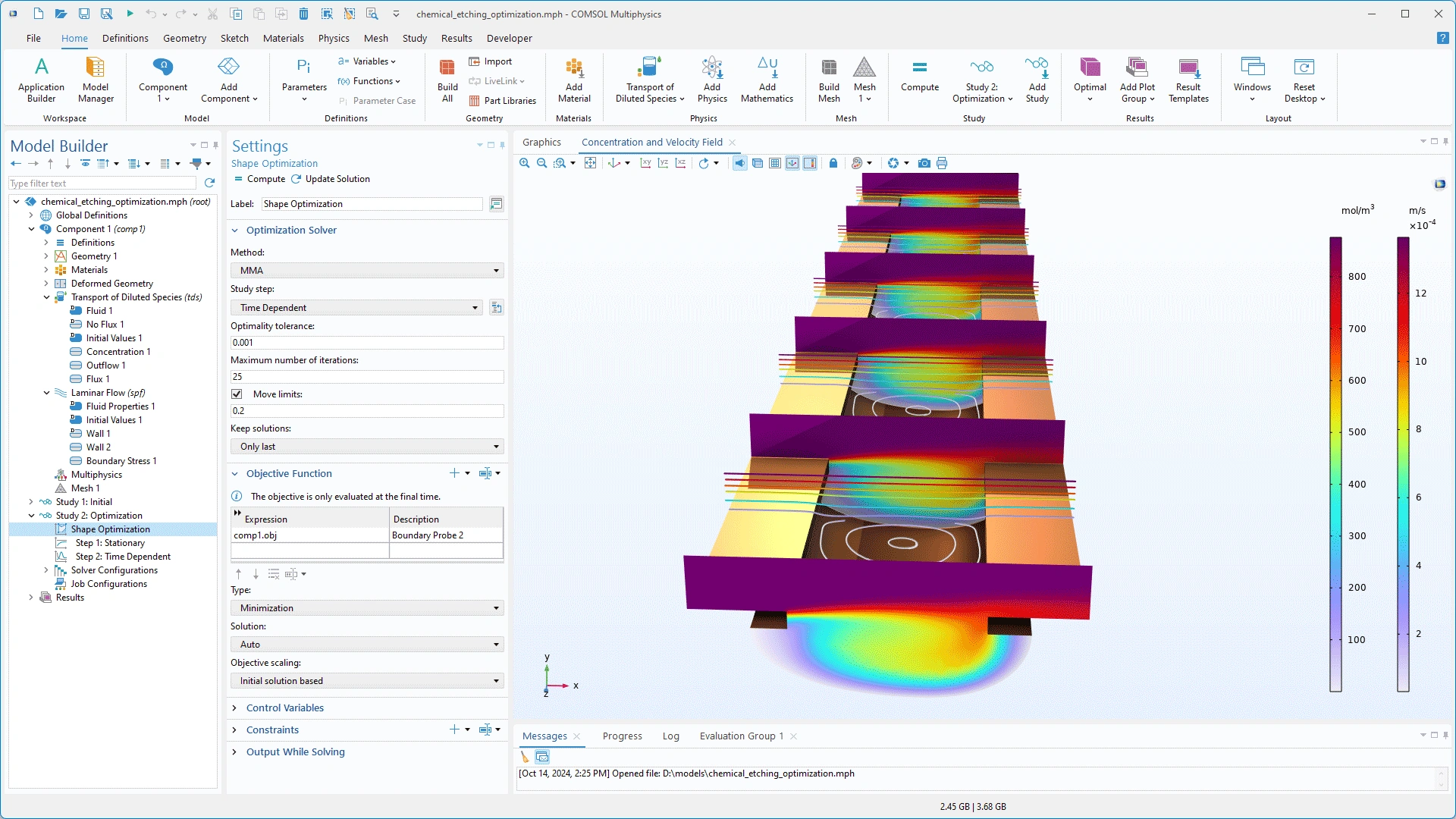
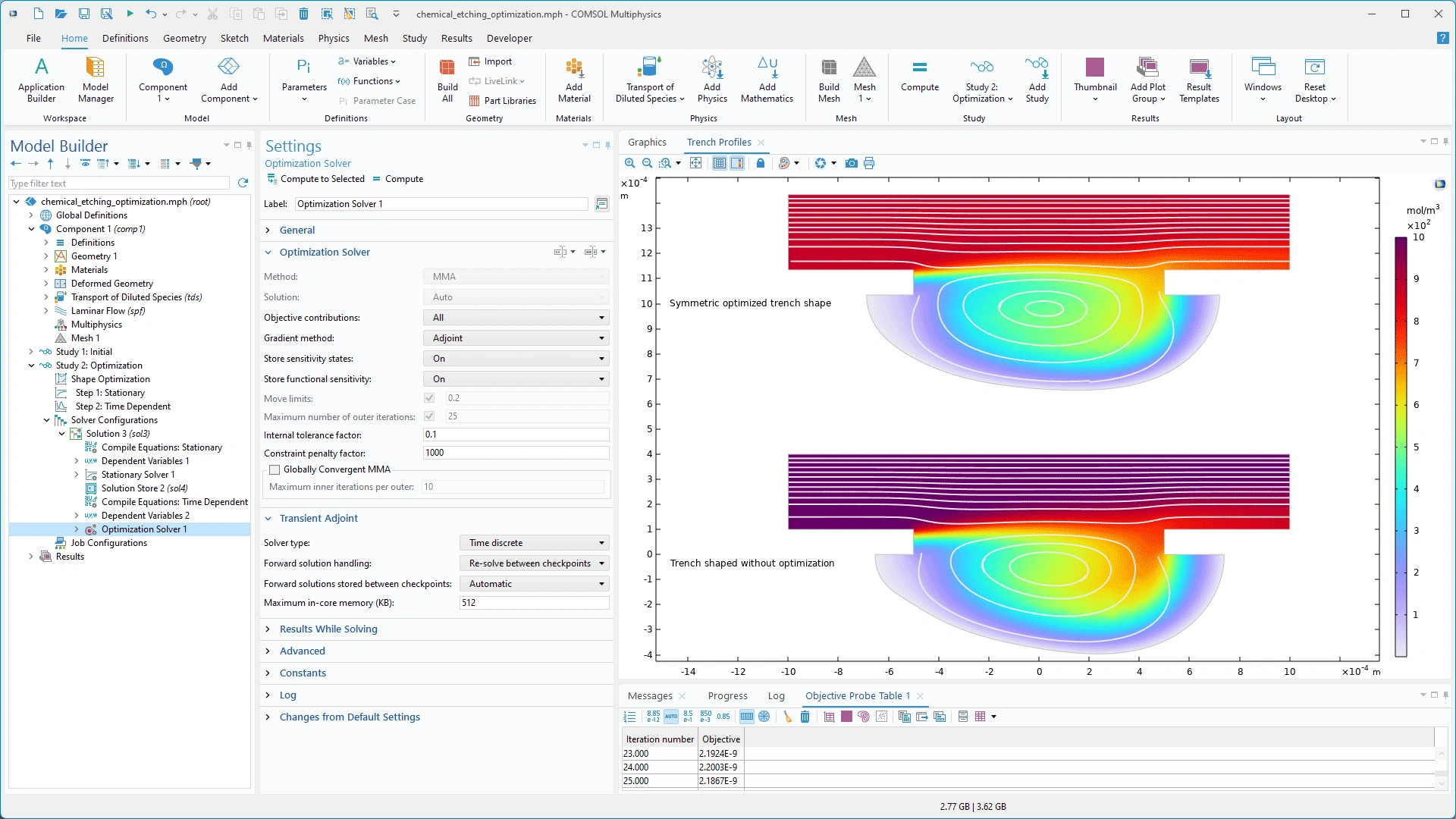
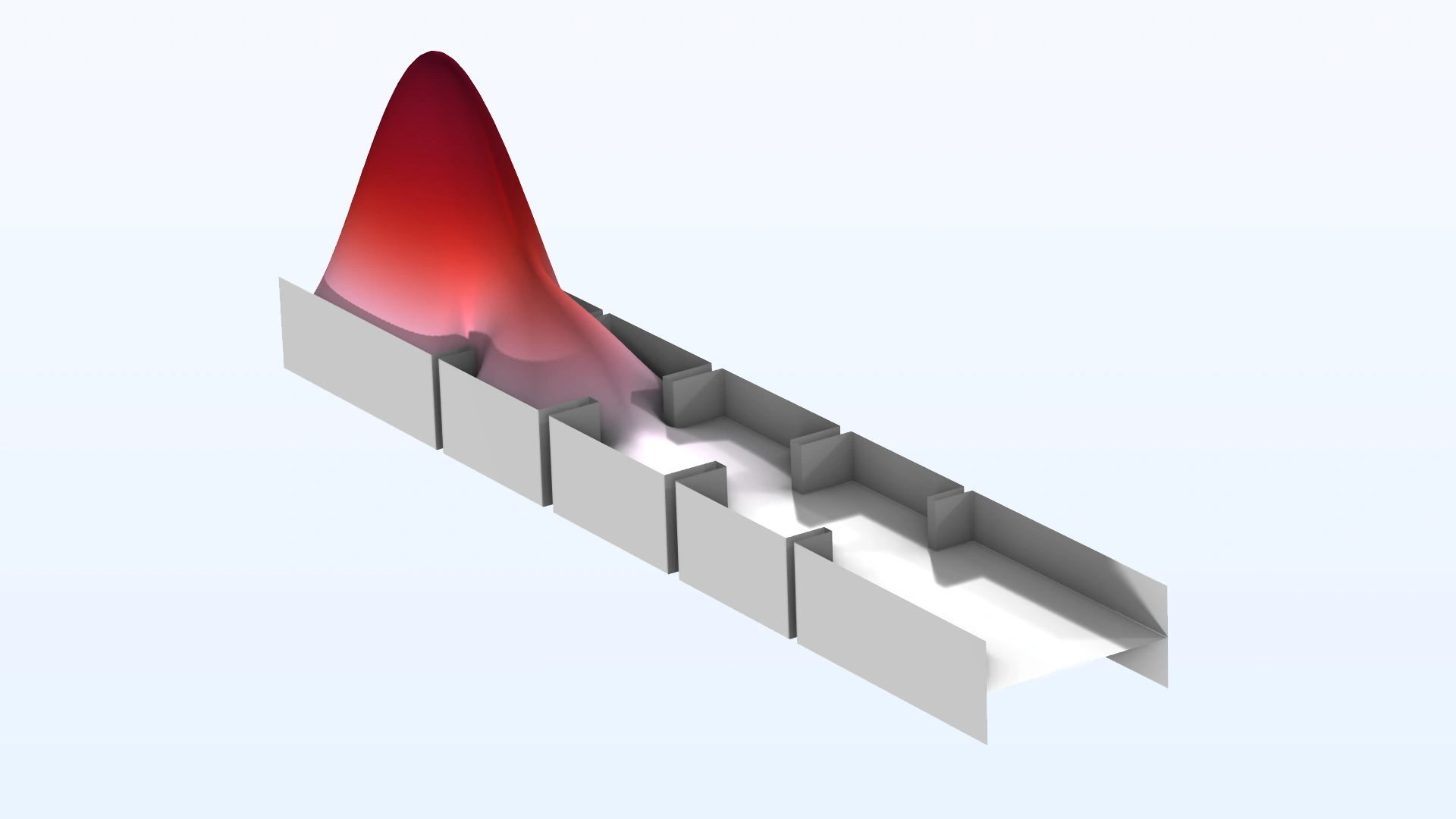
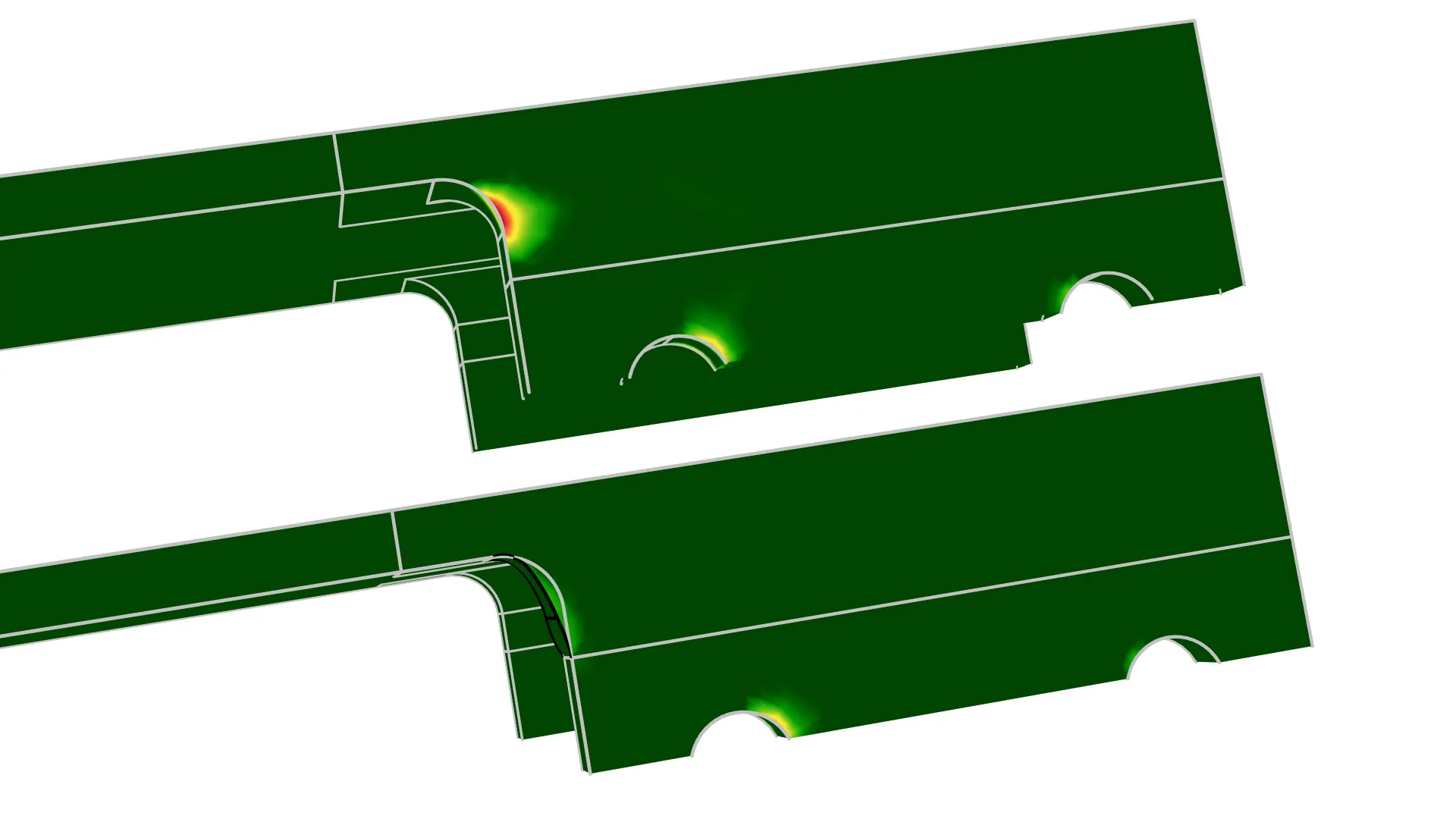
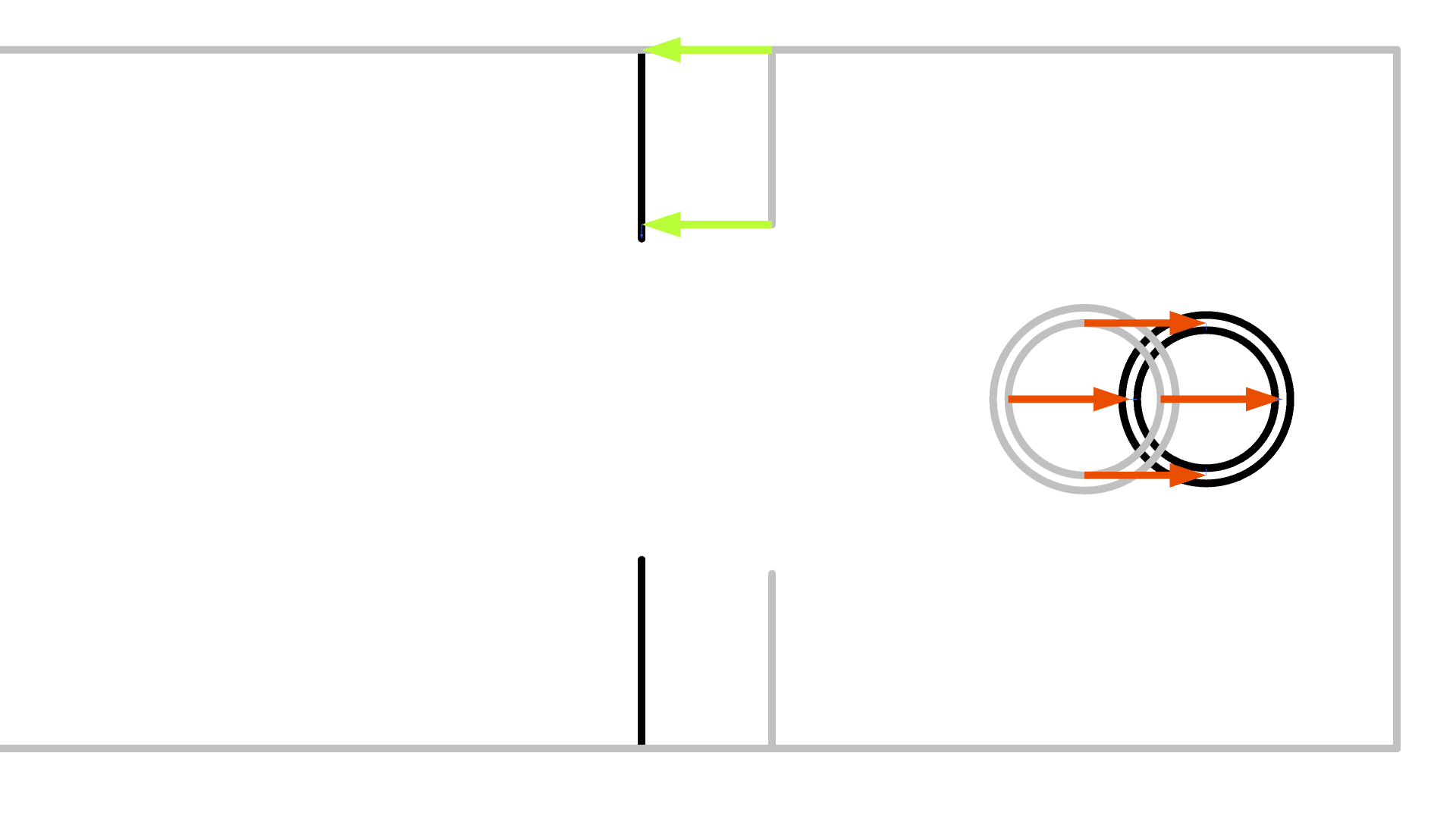
Configuración para el paso de estudio Shape Optimization utilizando un paso de estudio Time Dependent para la optimización de un proceso de grabado químico donde el objetivo es obtener una zanja simétrica como resultado del grabado.
Mejoras varias
En versiones anteriores, las funciones Free Shape Boundary y Free Shape Shell permitían conservar la continuidad de la normal en todos los límites de simetría o en ninguno. En esta versión, estas funciones se han actualizado y ahora es posible seleccionar para qué límites se conservará la simetría. Las funciones Polynomial Boundary y Polynomial Shell también se han actualizado para incluir compatibilidad con la conservación de la normal en bordes fijos en 3D. Además, la función Control Function se ha mejorado con compatibilidad con un valor inicial no uniforme y una interfaz de usuario rediseñada. Por último, la función Global Least-Squares Objective se ha trasladado a Global Definitions.
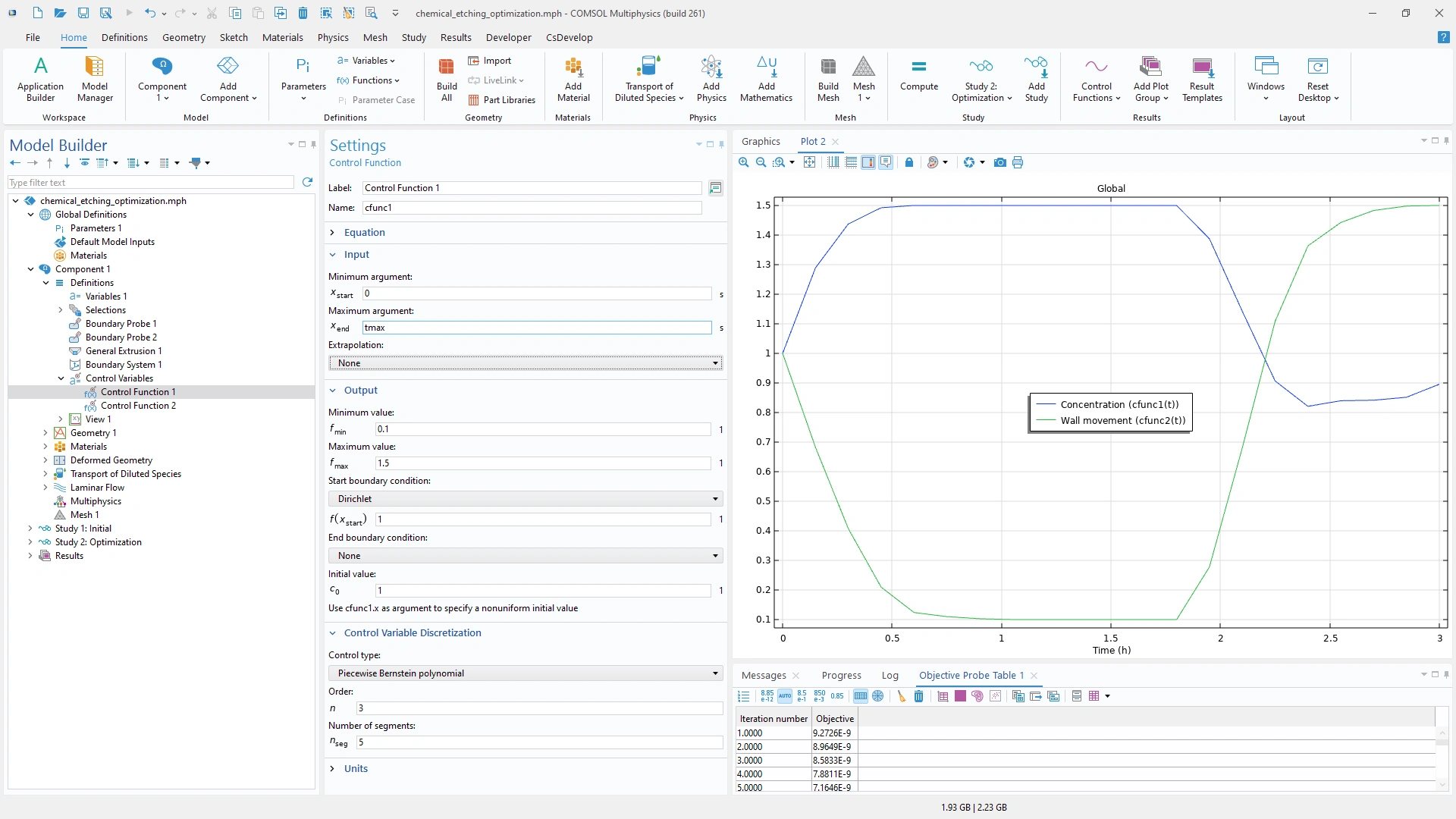
La función Control Function ahora admite cantidades físicas, un valor inicial no uniforme y configuraciones de extrapolación.
Nuevos modelos tutoriales
|
Pyrolysis of Wood with Time-Integrated Objective |
Optimization of Chemical Etching |
|
Optimization of the Solder Ball Array to Minimize Chip Warpage |
Bow Tie Antenna Optimization |
|
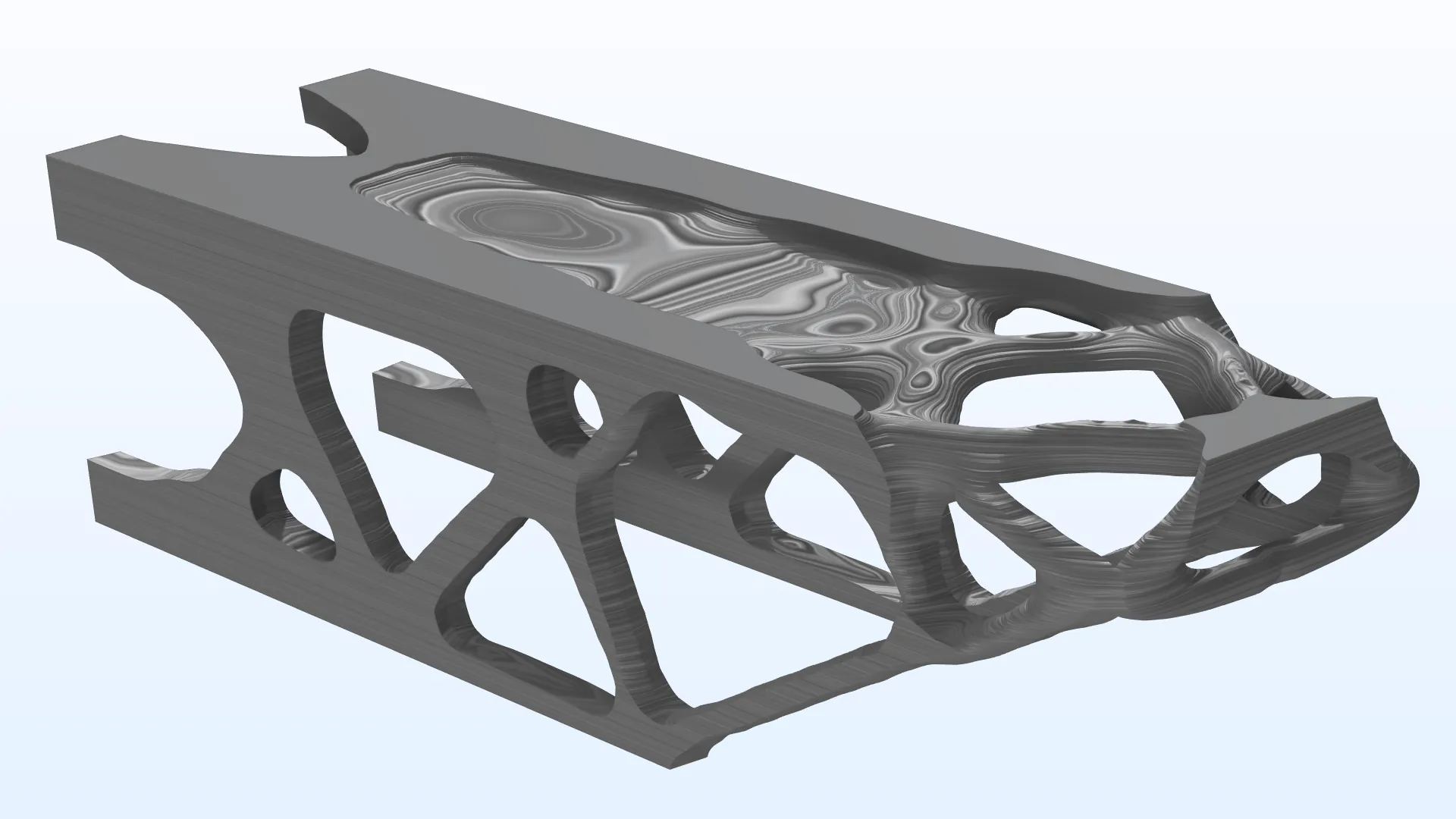
Topology Optimization of an MBB Beam with a Maximum Length Scale |
Optimization of a Waveguide Iris Bandpass Filter — EGO Version |
6.2
NOVEDADES
Paso de estudio Stationary Then Eigenfrequency
Un nuevo paso de estudio Stationary Then Eigenfrequency permite resolver consecutivamente un estudio Stationary y uno Eigenfrequency en un solo paso de estudio. Esta funcionalidad, de forma predeterminada, utiliza Stationary Solver para resolver las variables dependientes asociadas con las interfaces de optimización de forma y topología y usa Eigenfrequency Solver para resolver las variables dependientes asociadas con las interfaces de física. Esta funcionalidad es generalmente aplicable y podría usarse para maximizar la frecuencia propia más baja para una aplicación en mecánica estructural o para diseñar bandas prohibidas. Téngase en cuenta que el nuevo paso de estudio Stationary Then Eigenfrequency resuelve diferentes conjuntos de variables dependientes en los resolvedores estacionario y de frecuencias propias, lo que lo hace inadecuado para maximizar, por ejemplo, cargas de pandeo.
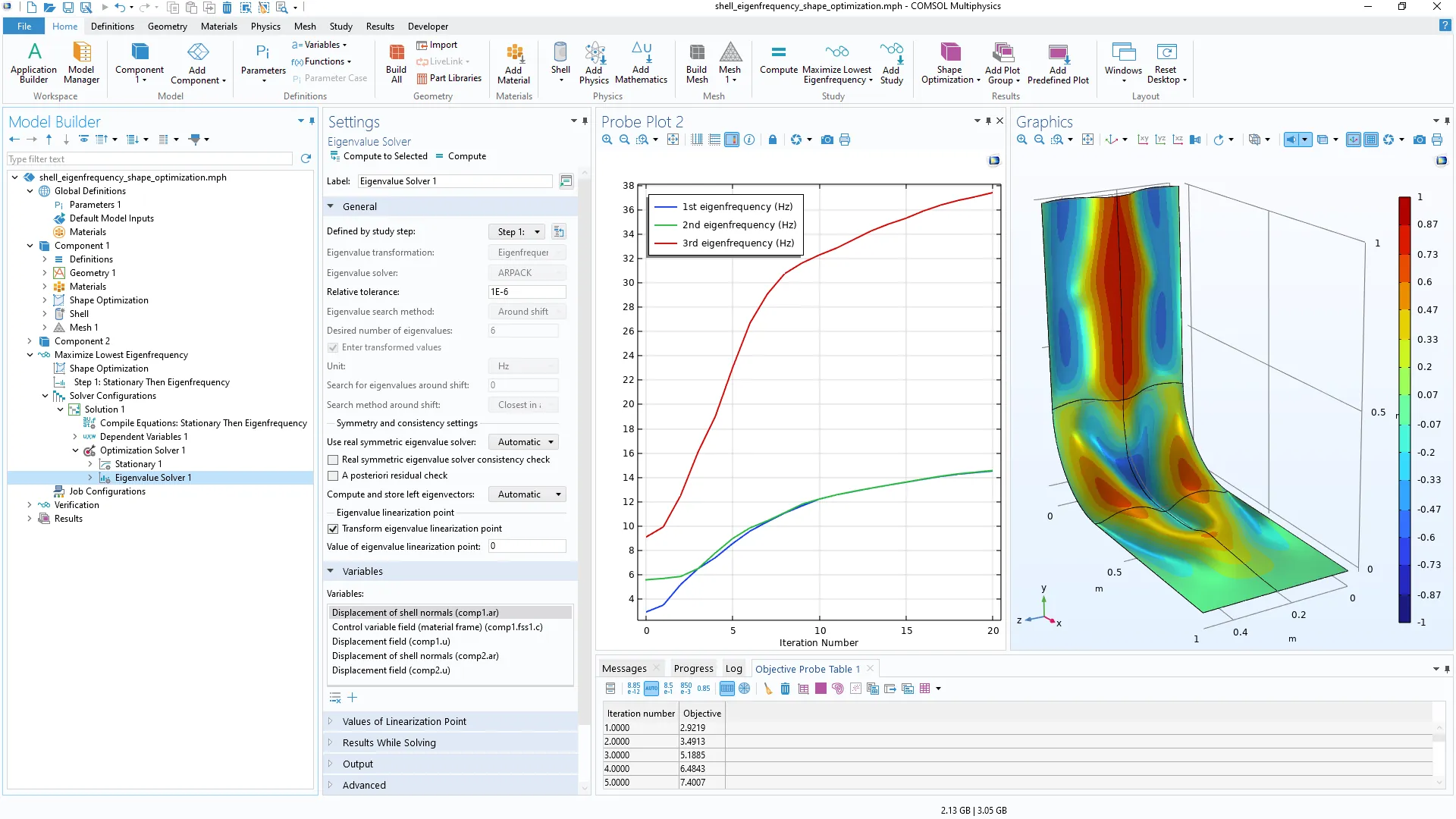
El nuevo paso de estudio Stationary Then Eigenfrequency se combina con la función Free Shape Shell para maximizar la frecuencia propia de una cáscara. El modelo también utiliza la nueva función Mirror Symmetry.
Estimación de parámetros
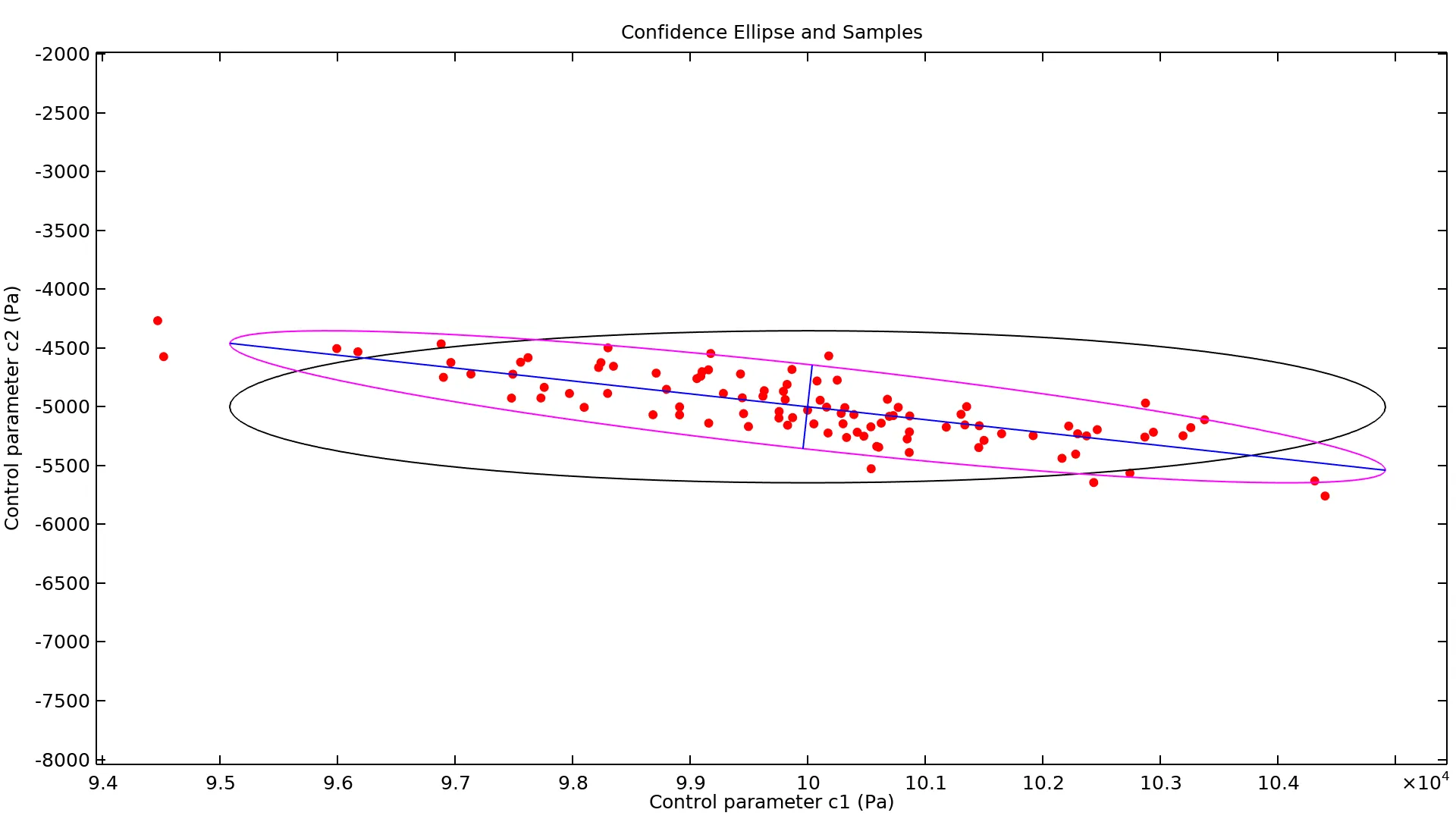
La función Global Least-Squares Objective y el paso de estudio Parameter Estimation ahora proporcionan una columna Varince para especificar la varianza de las mediciones individuales. Alternativamente, la varianza se puede estimar automáticamente y, en cualquier caso, los resultados se pueden utilizar para estimar la incertidumbre del resultado de la estimación de parámetros. El enfoque más simple es calcular intervalos de confianza para los parámetros estimados, pero los intervalos resultantes pueden no ser aplicables si los parámetros están correlacionados. Por lo tanto, se ha añadido la capacidad de exportar la matriz de covarianza y está disponible con el método de optimización de Levenberg-Marquardt. Esta capacidad proporciona una evaluación más detallada de la incertidumbre de la producción que utilizar los intervalos de confianza de los parámetros estimados. Además, se ha añadido soporte para límites al método de optimización Levenburg-Marquardt, lo que puede mejorar la solidez de los modelos no lineales.
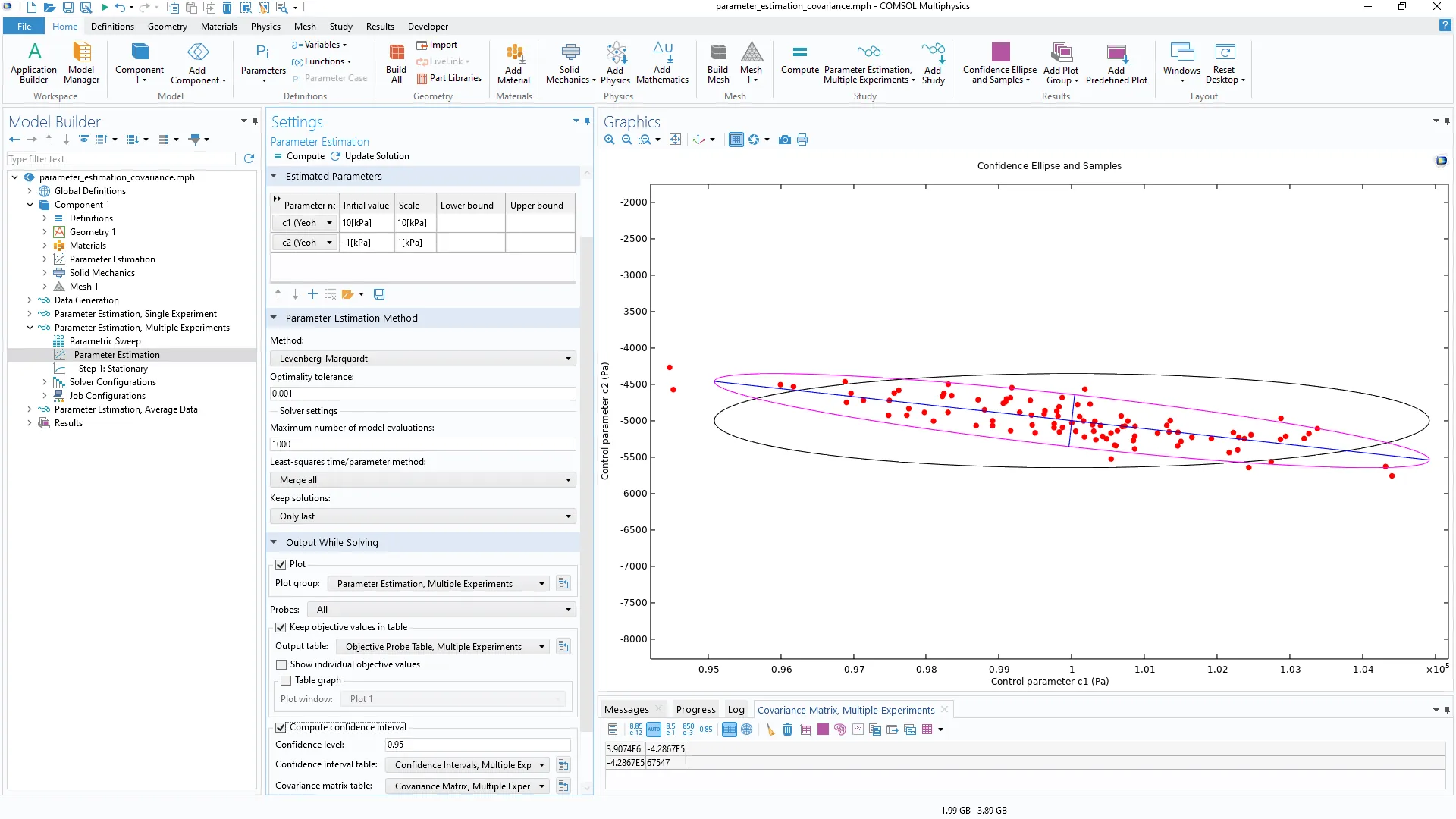
El cálculo de la matriz de covarianza se puede habilitar en la sección Output While Solving de los nodos de estudio Optimization and Parameter Estimation. El nuevo modelo Parameter Estimation with Covariance Analysis verifica que la matriz de covarianza proporciona una representación más ajustada de la incertidumbre que los intervalos de confianza (representados con líneas negras en la imagen).
Actualizaciones de optimización de topología y forma
Para la optimización de la topología, se han añadido nuevas funciones Mirror Symmetry y Sector Symmetry para simplificar la configuración de modelos donde se requiere un diseño simétrico pero donde no se espera que los efectos de ciertos fenómenos físicos sean simétricos. En algunos casos, estas características se pueden utilizar para reducir la cantidad de soluciones o casos de carga por iteración, lo que conduce a un mejor rendimiento. Además, las características de optimización de la forma ahora incluyen la capacidad de establecer el desplazamiento máximo para componentes individuales, y también es posible imponer una interpretación euclidiana del desplazamiento máximo, en lugar de la interpretación anterior taxicab (en forma de caja).
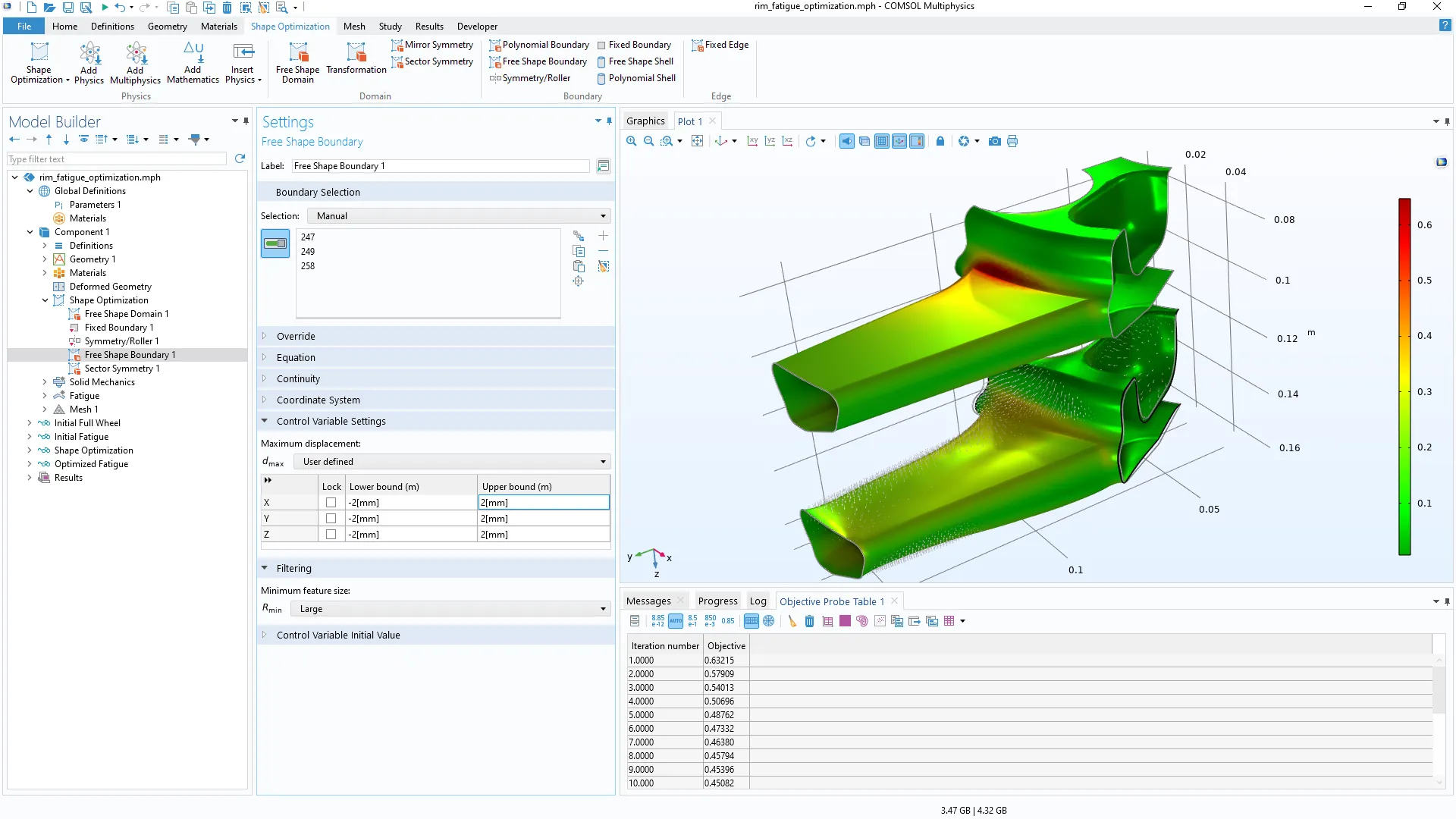
Las nuevas configuraciones de optimización de forma para un desplazamiento máximo se muestran en el modeloWheel Rim — Stress Optimization with Fatigue Evaluation y la nueva pestaña Shape Optimization en la cinta.
Actualizaciones de propósito general
- La funcionalidad Control Variable Field incluye soporte para agrupar entidades adyacentes utilizando la nueva discretización constante geométrica.
- La configuración de la función Control Function incluye opciones adicionales y una coherencia mejorada entre las funciones polinómicas y la regularización de Helmholtz.
- Las nuevas pestañas de cinta Shape Optimization, Topology Optimization y Parameter Estimation aparecen cuando las funciones están en uso, lo que proporciona una mejor coherencia con el árbol del Model Builder.
- Las funciones Control Function y Control Variable Field se han movido a la rama Definitions en el árbol del Model Builder.
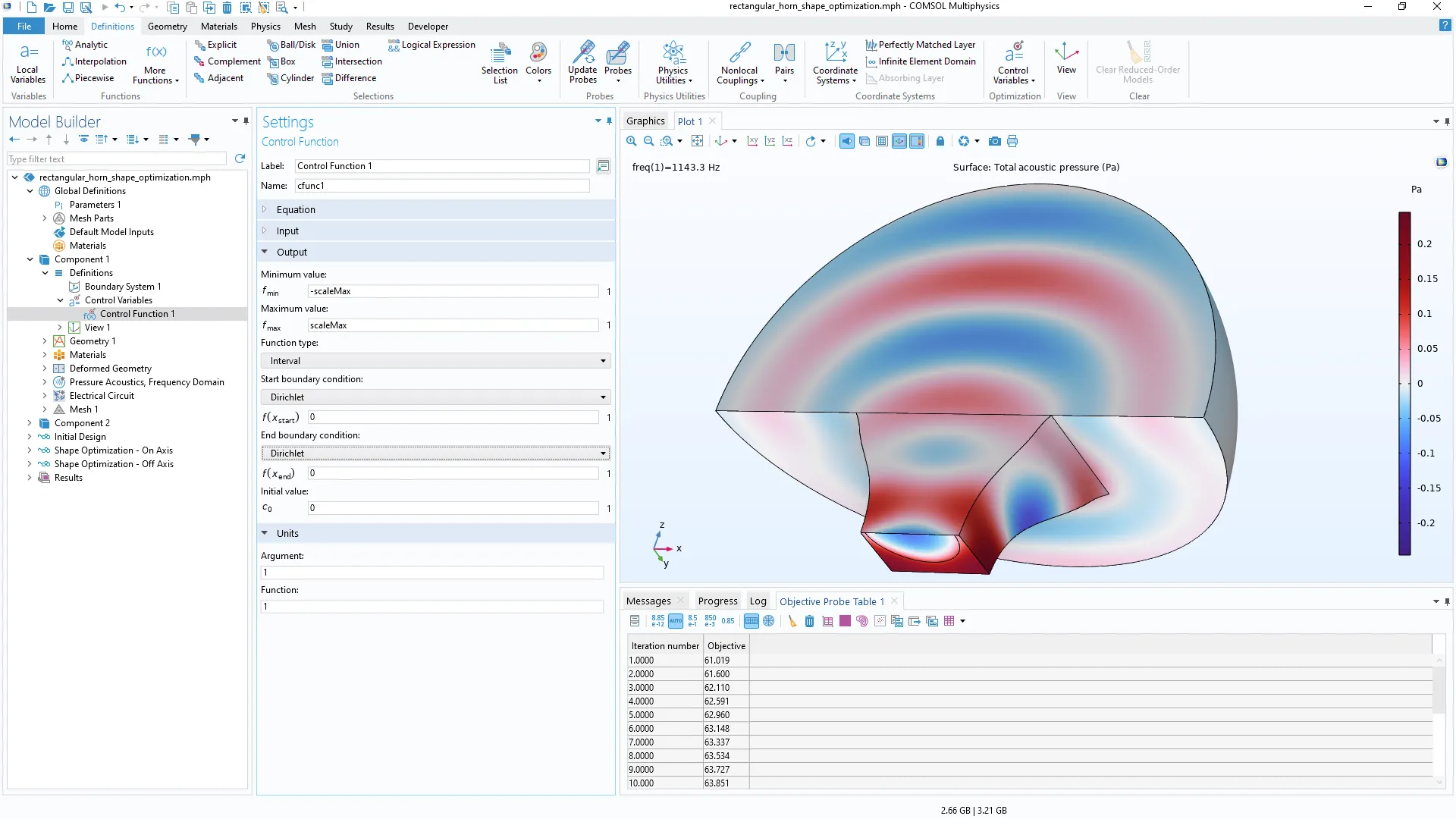
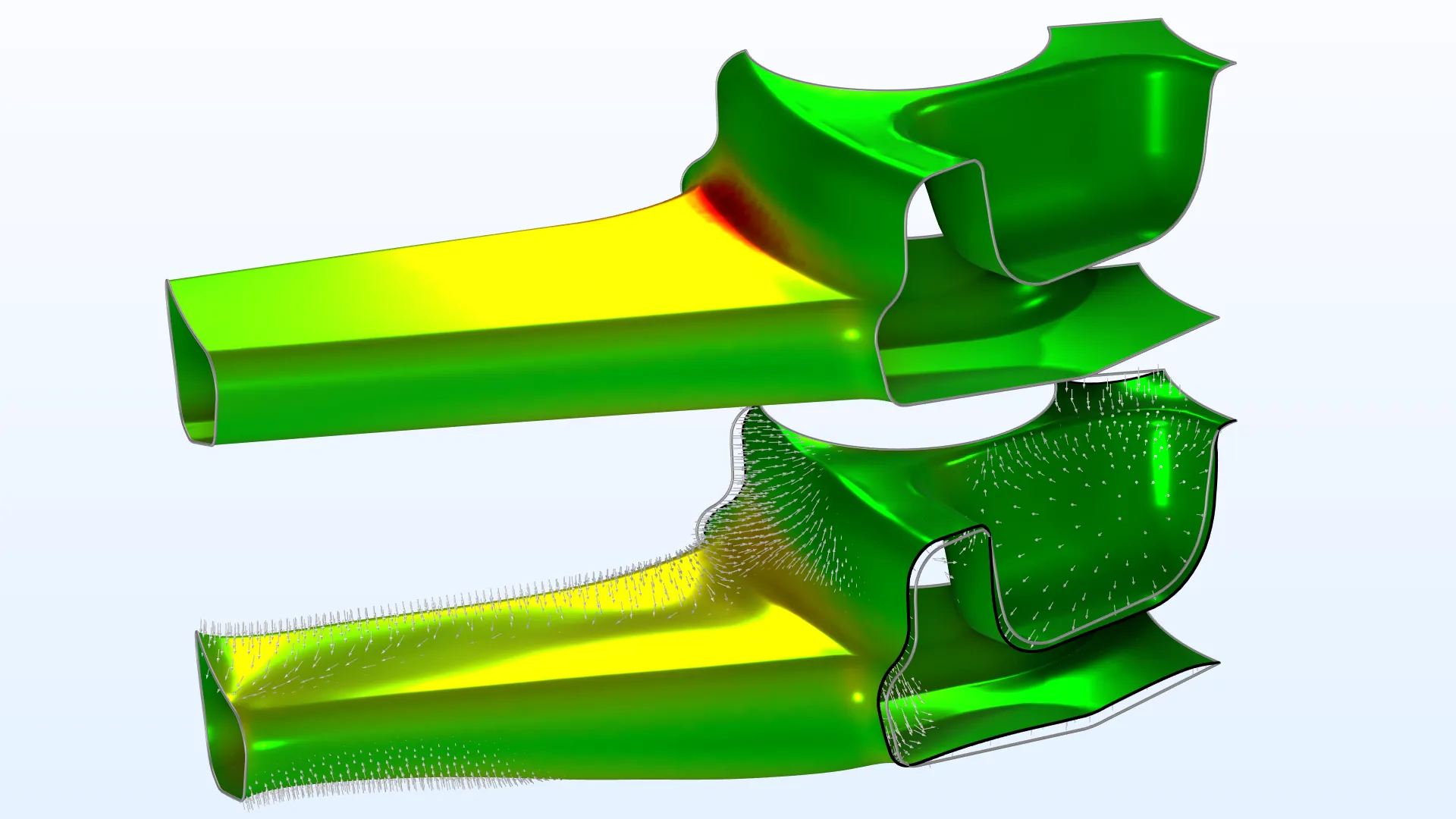
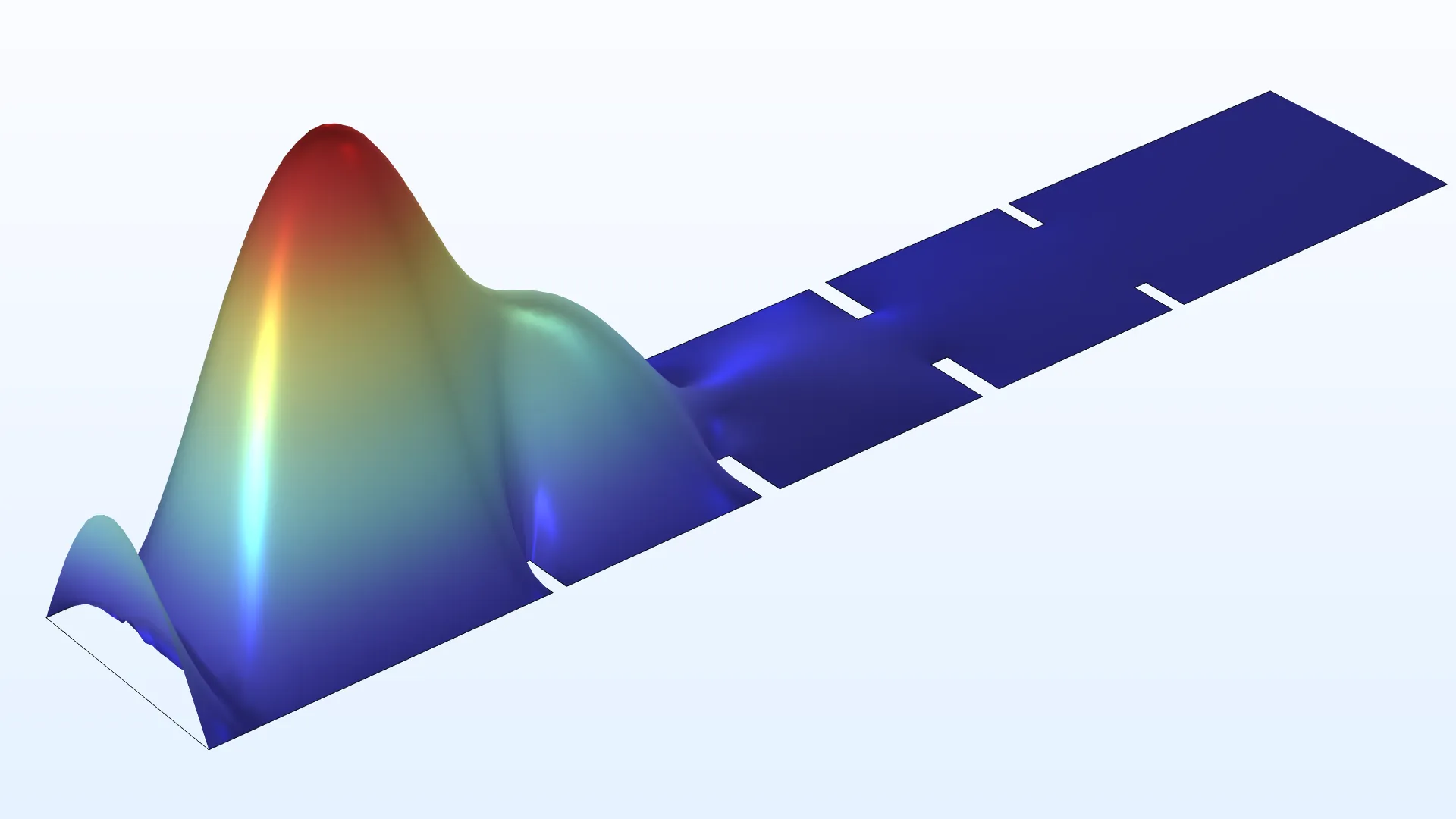
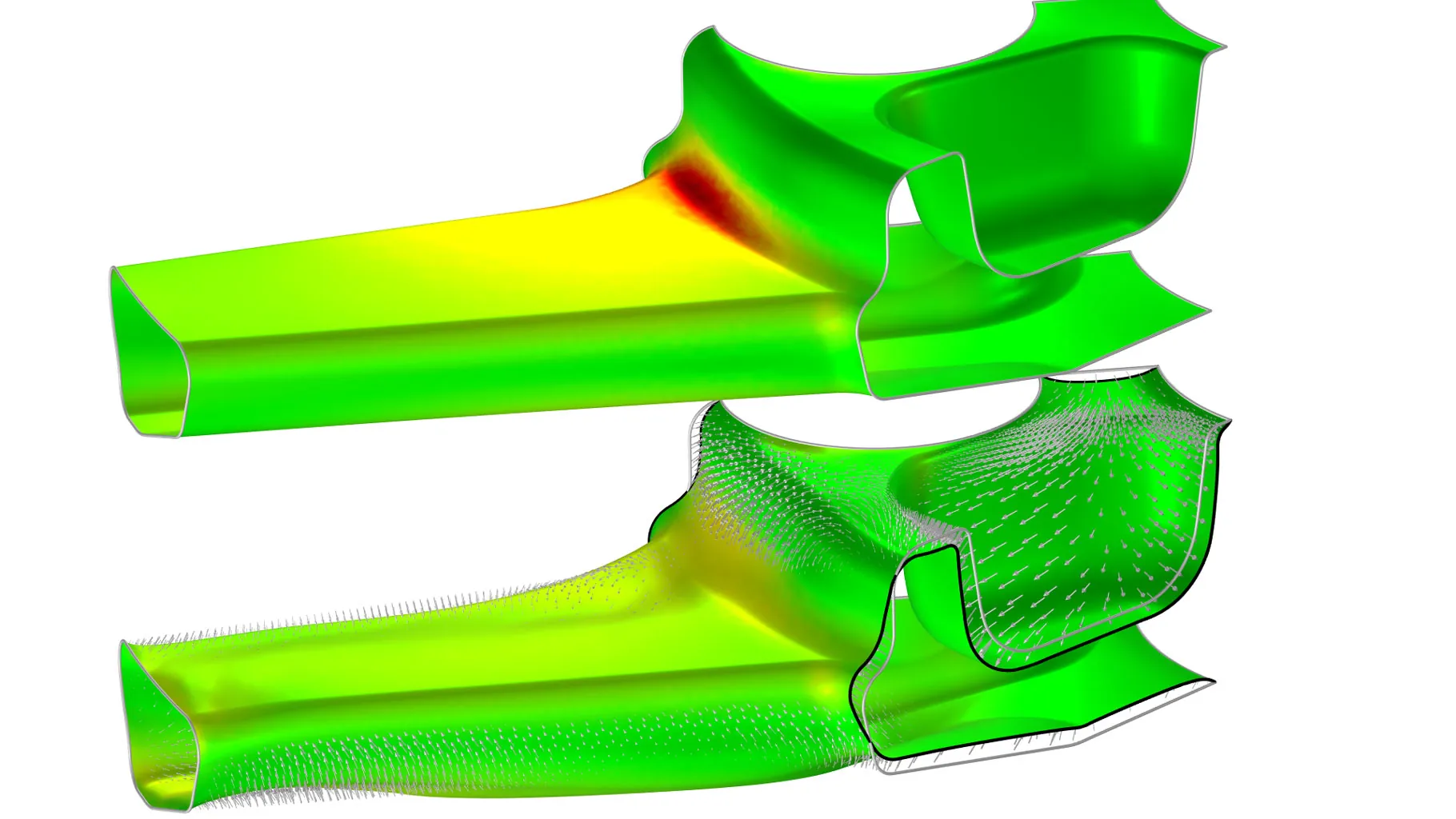
Las nuevas condiciones de contorno para la función Control Function se muestran en el modelo Shape Optimization of a Rectangular Loudspeaker Horn in 3D. Se puede acceder a las funciones Control Variable Field y Control Function desde el botón Control Variables en la pestaña Definitions.
Nuevos modelos tutoriales
|
Tweeter Dome and Waveguide Shape Optimization |
Wheel Rim — Stress Optimization with Fatigue Evaluation |
|
Wheel Rim — Topology Optimization with Milling Constraints |
Maximizing the Eigenfrequency of a Shell |
|
Optimal Control for Heating of a Rod |
Optimization of a Waveguide Iris Bandpass Filter — Transformation Version |
|
Optimization of a Photonic Crystal for Signal Filtering |
Maximizing the Eigenfrequency of a Beam |
|
Bracket — Eigenfrequency Shape Optimization |
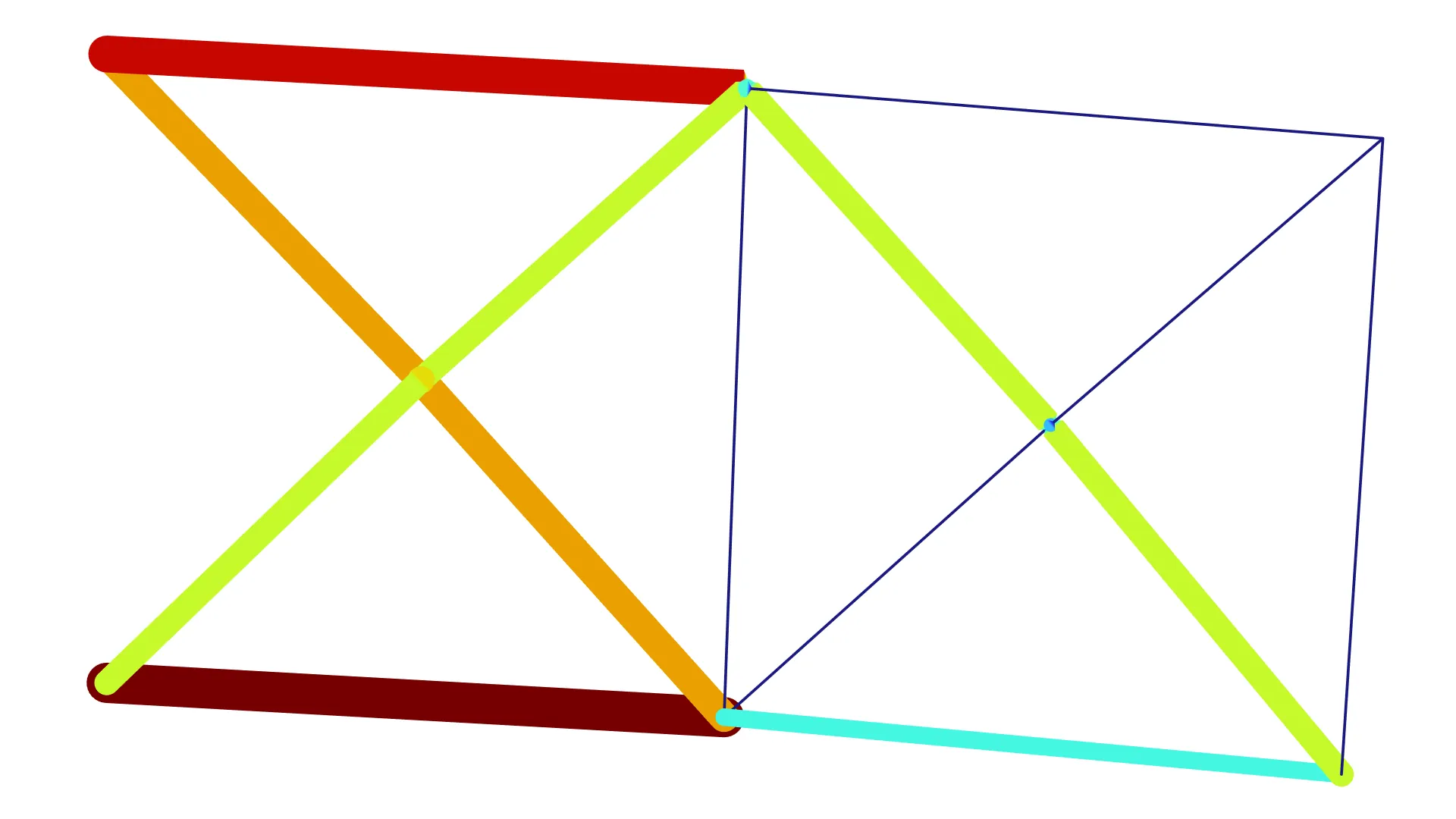
Ten-Bar Truss Optimization |
|
Parameter Estimation with Covariance Analysis* |
6.1
NOVEDADES
La versión 6.1 proporciona restricciones de fresado para la optimización topológica, soporte mejorado para preservar la continuidad de curvas y superficies para la optimización de formas, y una nueva función para la optimización de formas de frecuencias propias para láminas estructurales.
Restricciones de fabricación para la optimización de topología
La optimización de la topología está asociada con una libertad de diseño extrema. Esto puede producir un rendimiento extremo pero también piezas de geometría compleja que son difíciles de usar en las técnicas de fabricación convencionales. La función Density Model existente ahora incluye la funcionalidad de restricción de fresado para garantizar la compatibilidad con las técnicas de fabricación convencionales. Puede verse esta función en el nuevo modelo "Topology Optimization of a Beam with milling Constraints" y en varios modelos de mecánica estructural actualizados.
|
|
|
|
La optimización de la topología de una rueda se muestra en el nuevo modelo de tutorial Wheel Rim — Topology Optimization with Milling Constraints. Se modela la rueda completa, con simetría de sector impuesta para la optimización de la forma. La llanta de la rueda está optimizada para la rigidez con respecto a 12 casos de carga, y la optimización incluye restricciones de fresado en las direcciones axiales (izquierda). El resultado correspondiente sin restricciones de fresado se muestra como referencia (derecha). |
|
Continuidad para la optimización de forma
Al realizar la optimización de formas, preservar la continuidad del vector normal es una forma de mantener curvas y superficies suaves en el modelo geométrico optimizado. Las funciones Free Shape Boundary y Free Shape Shell se han ampliado con soporte para preservar la continuidad del vector normal sobre los contornos Symmetry y Roller así como entre la selección de diferentes funciones Free Shape Boundary y Free Shape Shell. De manera similar, las versiones 2D de las funciones Polynomial Boundary y Polynomial Shell se han ampliado con soporte para preservar la continuidad del vector normal sobre los contornos Symmetry y Roller, así como entre entidades en la selección y junto a puntos fijos. El modelo "Design Optimization of a Beam" se ha actualizado para usar esta nueva funcionalidad.
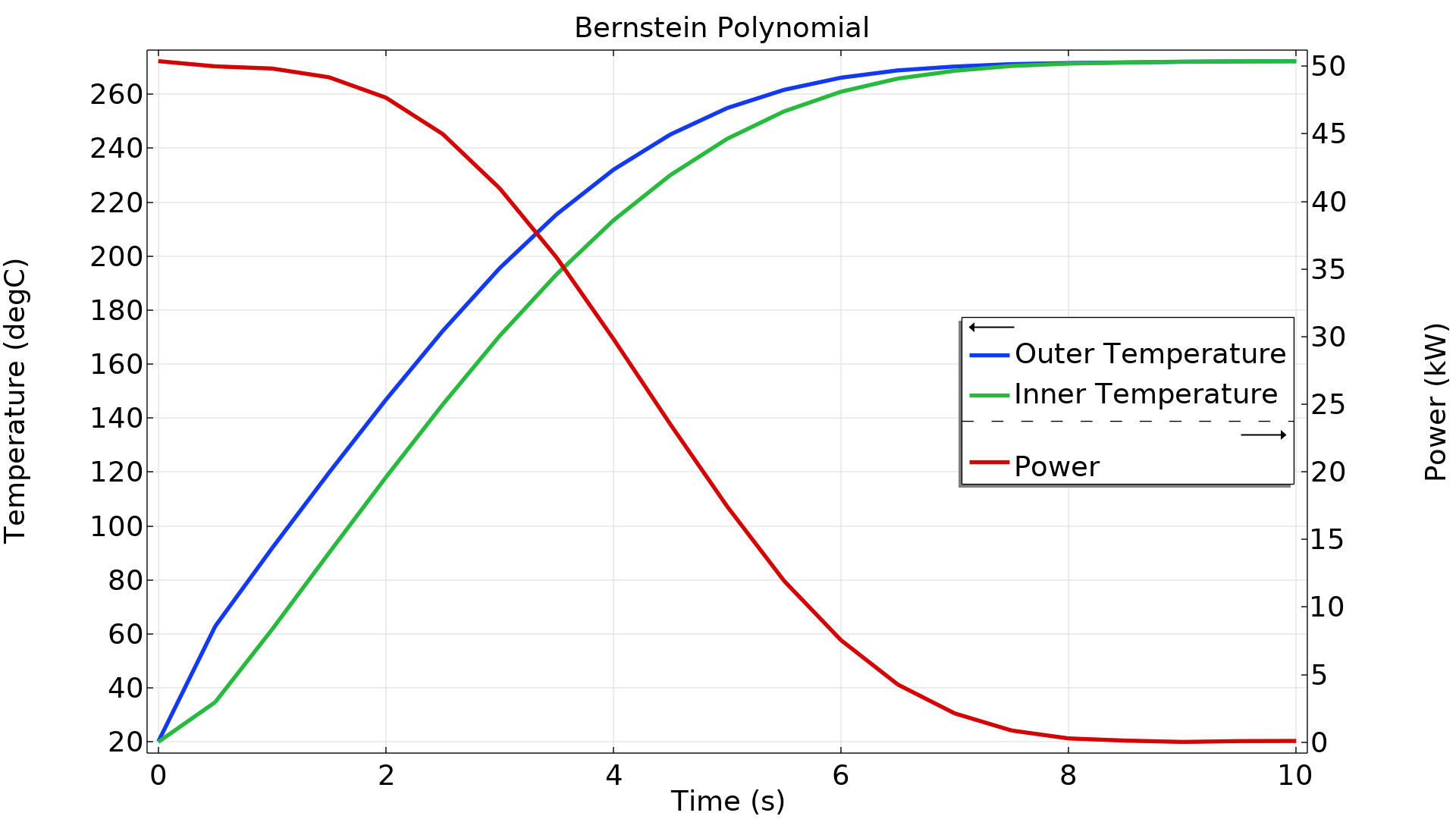
Además, la característica Control Function ahora incluye una opción Piecewise Bernstein polynomial. Para este tipo de control, la pendiente es continua entre los polinomios. Esto es útil para aumentar la libertad de diseño sin introducir el ruido de alta frecuencia típicamente asociado con los polinomios de orden superior.
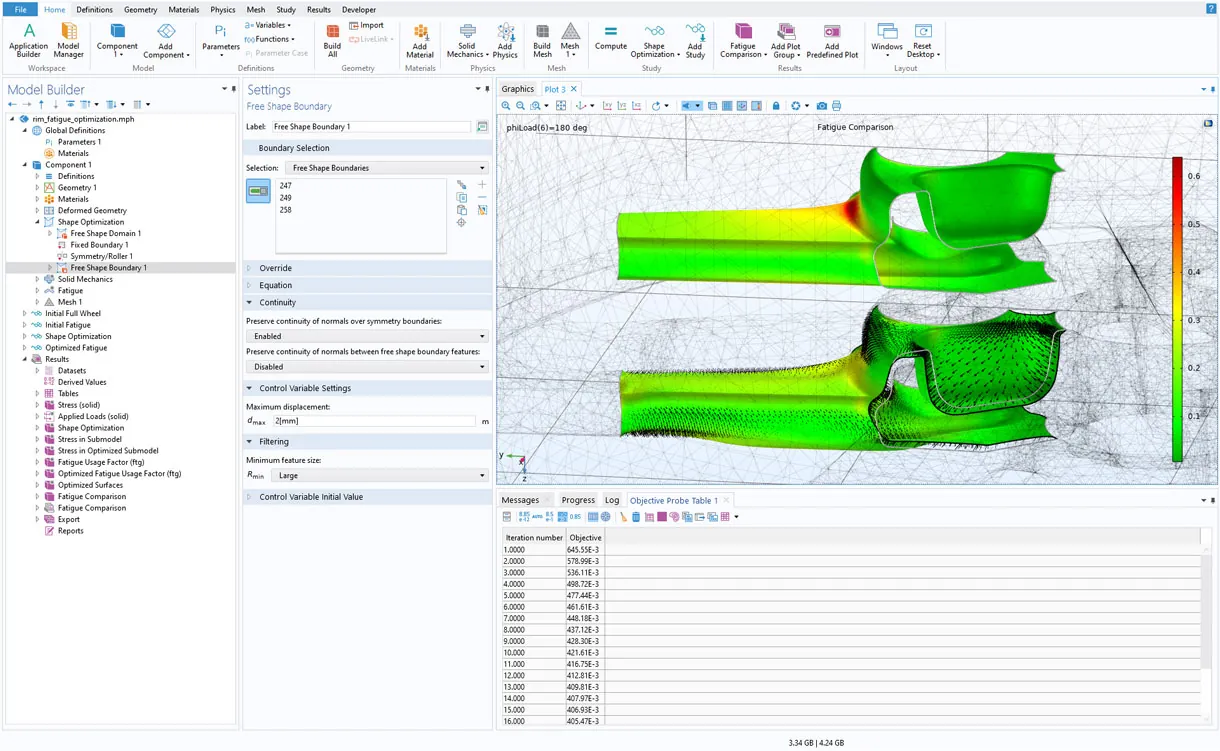
El nuevo modelo tutorial Wheel Rim — Stress Optimization with Fatigue Evaluation demuestra la optimización de la forma de una rueda con respecto a una aproximación de la tensión máxima. Se modela la rueda completa, con simetría de sector impuesta para la optimización de la forma. Además, se utiliza una malla más fina en el sector utilizado para la evaluación de la tensión, y la configuración de la función Límite de forma libre garantiza la continuidad del vector normal entre sectores. La optimización considera 6 casos de carga y optimiza para el peor de los casos mientras restringe la rigidez y la masa a los valores iniciales. Este es un enfoque heurístico para la optimización de fatiga, por lo que las propiedades de fatiga se evalúan antes y después de la optimización.
Optimización basada en gradientes de frecuencias propias para cáscaras
Las frecuencias propias ahora pueden estar sujetas a ciertos tipos de optimizaciones basadas en gradientes y, por ejemplo, pueden usarse para la optimización de la forma de las cáscaras estructurales. La característica Polynomial Boundary existente se ha ampliado para admitir 3D y se ha añadido una nueva funcionalidad Polynomial Shell a la interfaz de optimización de forma Shape Optimization. Puede verse una demostración de esta funcionalidad en el nuevo modelo tutorial "Maximizing the Eigenfrequency of a Shell".
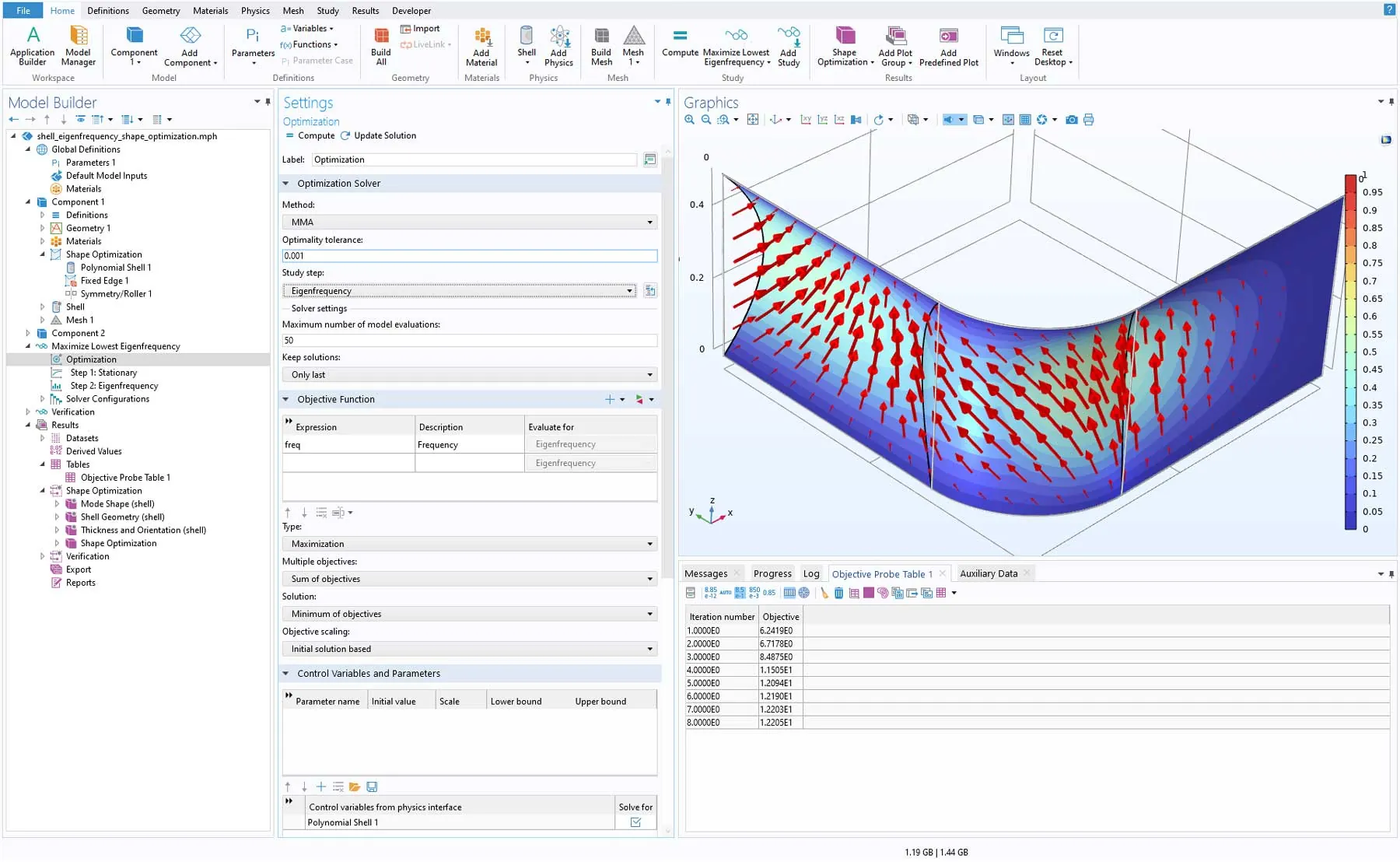
El modelo Maximizing the Eigenfrequency of a Shell muestra cómo utilizar la nueva funcionalidad Polynomial Shell para maximizar la frecuencia propia más baja de una cáscara.
Nuevos modelos tutoriales
|
Exporting and Importing a Topology-Optimized Hook |
Topology Optimization of a Torsion Sphere with Milling Constraints |
|
Topology Optimization of a Step Thrust Bearing |
Shape Optimization of a Step Thrust Bearing |
|
Topology Optimization of a Beam with Milling Constraints |
Design Optimization of a Beam |
|
Maximizing the Eigenfrequency of a Shell |
Topology Optimization of a Sound Partition Considering Acoustic–Structure Interaction |
|
Bracket — Stress Optimization with Fatigue Evaluation |
Wheel Rim — Stress Optimization with Fatigue Evaluation |
|
Wheel Rim — Topology Optimization with Milling Constraints |
6
NOVEDADES
La versión 6.0 ofrece una función de Transformación para configurar variaciones de forma simples, funcionalidad de estimación de parámetros renovada para análisis de objetivos de mínimos cuadrados, soporte mejorado para optimización transitoria y funciones de optimización de más fácil acceso.
Optimización de forma
Para la Optimización de forma existe una nueva funcionalidad Transformación para configurar rápidamente variaciones de formas simples. Esta admite traslación, escalado y rotación, así como sistemas de coordenadas personalizados. La simplicidad de las variaciones de forma garantiza que sea posible construir una representación CAD del resultado de la optimización. Puede verse esta nueva funcionalidad en los modelos existentes Optimization of a Photonic Crystal for Signal Filtering y Optimization of a Photonic Crystal for Demultiplexing, así como en un nuevo modelo llamado Optimization of a Waveguide Iris Bandpass Filter - Transformation Version.
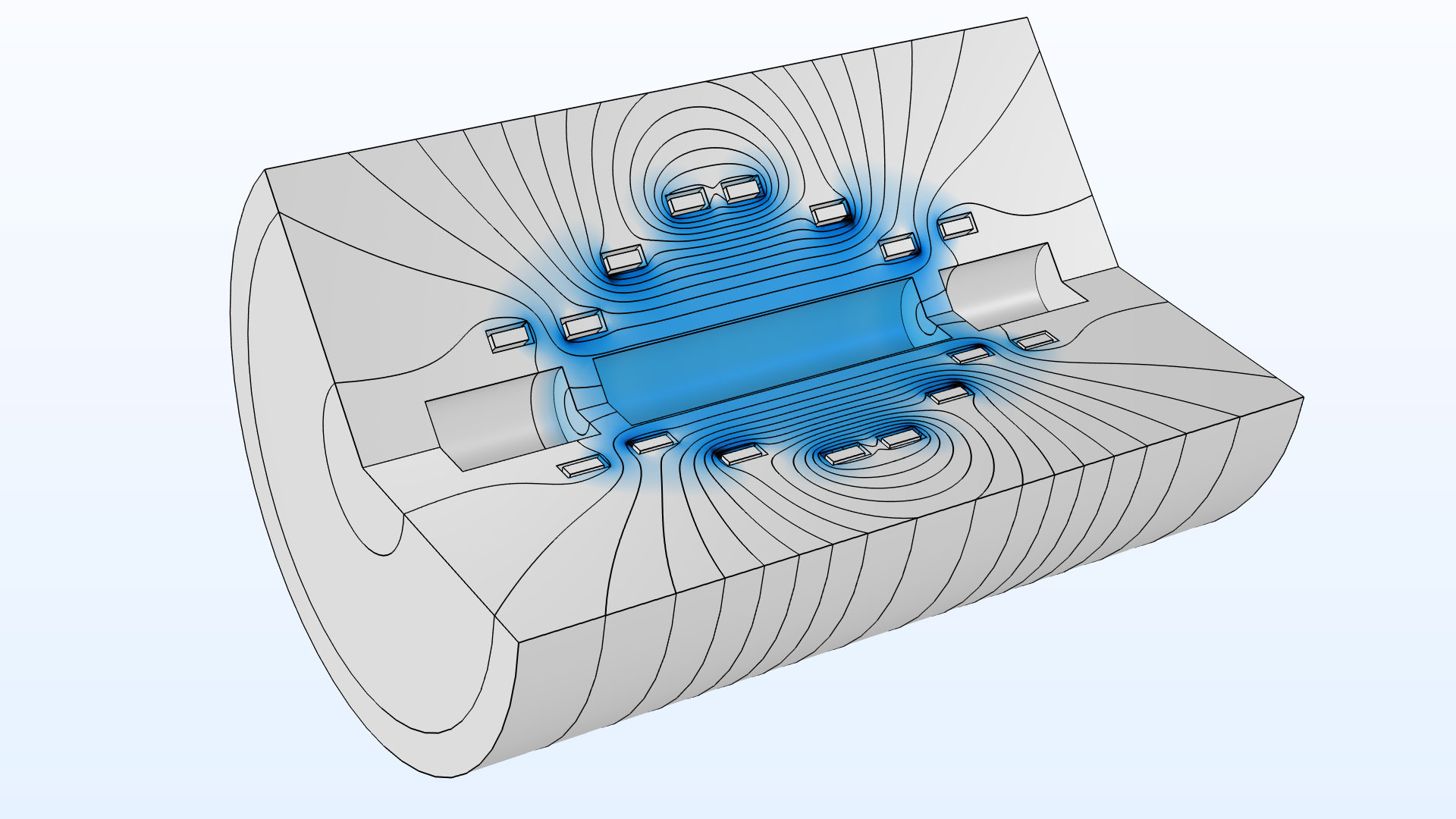
La densidad de flujo magnético de una bobina electromagnética 2D revolucionada.
Estimación de parámetros
La configuración de los modelos de estimación de parámetros se ha simplificado utilizando un conjunto de nuevas herramientas e interfaces. Una nueva funcionalidad Global Least-Squares Objective está disponible a través del nodo Componente. Esta función tiene una interfaz de usuario mejorada en relación con la función anterior (que todavía está disponible a través de la interfaz de Optimización). Además, también se ha introducido un nuevo paso de estudio Estimación de parámetros, mientras que el antiguo paso de estudio Estimación de parámetros se ha renombrado como Ajuste de curvas . Con este nuevo paso de estudio, puede configurarse un objetivo de mínimos cuadrados directamente en el paso de estudio, sin necesidad de añadir una interfaz de Optimización general, y también se puede utilizar con características objetivas de mínimos cuadrados. Varios modelos tutoriales hacen uso de la nueva funcionalidad de estimación de parámetros, que incluyen (pero no se limitan a) los modelos Impedance Tube Parameter Estimation with Data Generation, Mooney-Rivlin Curve Fit, Estimation of Corrosion Kinetics Parameters y Modeling Impedance in the Lithium-Ion Battery.
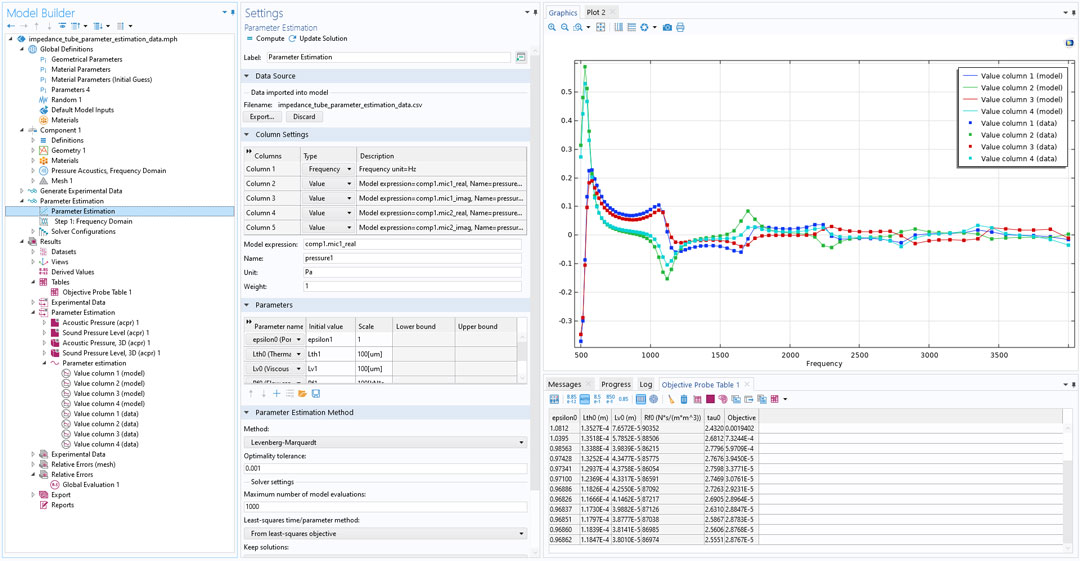
El modelo Estimación de parámetros del tubo de impedancia con generación de datos demuestra cómo utilizar el nuevo paso de estudio Estimación de parámetros para estimar parámetros poroacústicos en función de las mediciones del tubo de impedancia.
Optimización transitoria
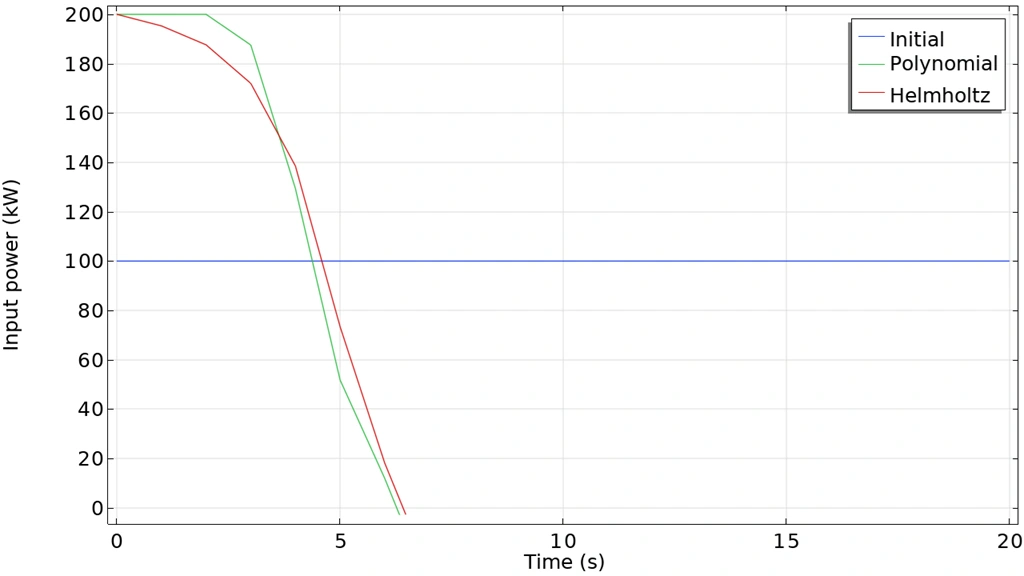
La ejecución de análisis de sensibilidad transitoria es más sólida con mejoras en la configuración del resolvedor. Se puede lograr una solidez adicional mediante el uso de pasos de tiempo fijos y/o una nueva configuración de resolvedor manual que permite resolver el problema transitorio adjunto usando los mismos pasos de tiempo que el problema directo. Por separado, una nueva funcionalidad de Función de control permite controlar variables que varían en el tiempo. El argumento puede ser el tiempo, como en el modelo Optimal Control for Heating of a Cylinder, o puede elegirse arbitrariamente como se muestra en el modelo Shape Optimization of a Rectangular Liudspeaker Horn in 3D, donde la función se utiliza para la optimización de la forma. El modelo de Optimization of a Tesla Microvalve with Transient Flow también hace uso de las mejoras para la optimización transitoria.
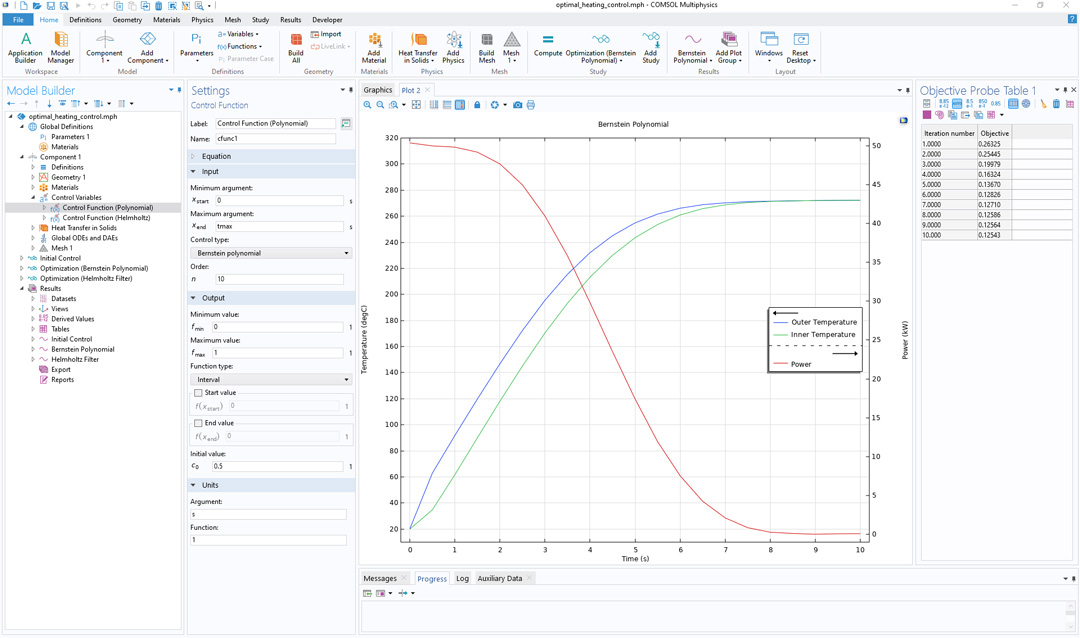
El modelo de control óptimo para el calentamiento de un cilindro demuestra cómo utilizar la funcionalidad de Función de control para alcanzar una determinada temperatura lo más rápido posible. En este caso, la función se utiliza con el tiempo como argumento.
Funciones de optimización reubicadas
Además de la funcionalidad nueva y actualizada, la forma de acceder a las interfaces de usuario del módulo de optimización ha cambiado. Las características de optimización que estaban ubicadas debajo del nodo Definiciones se han elevado para existir en el mismo nivel que las interfaces físicas. Este cambio facilita el acceso a las funciones de optimización y también las hace más visibles en el árbol del modelo.
Nuevos modelos tutoriales
|
Loudspeaker Spider Optimization |
Shape Optimization of Coils |
|
Optimization of a Waveguide Iris Bandpass Filter — Transformation Version |
Topology Optimization of a Drone |
|
Petzval Lens Optimization |
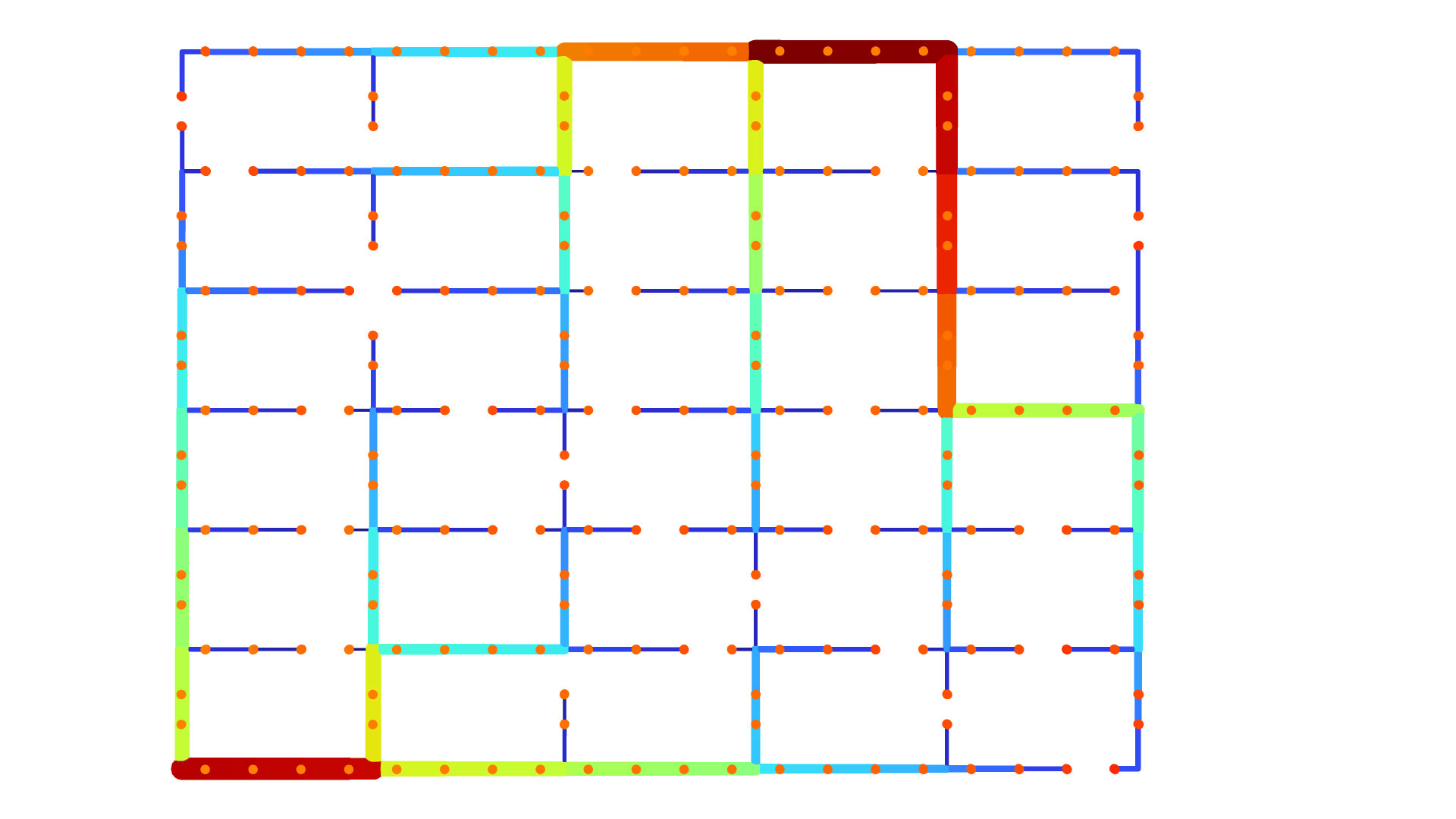
Topology Optimization of a District Heating Network |
|
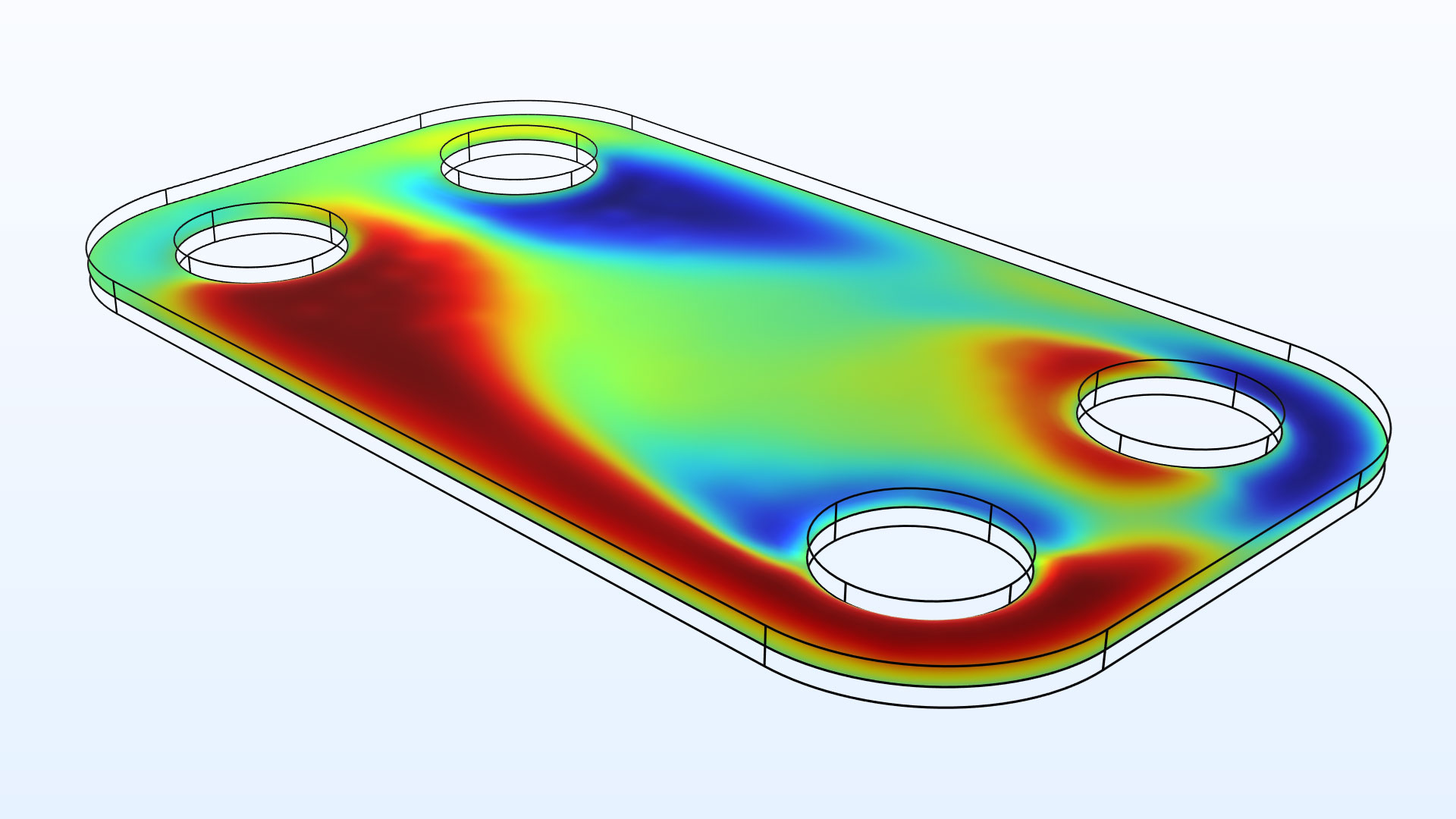
Shape Optimization of a Plate Heat Exchanger |
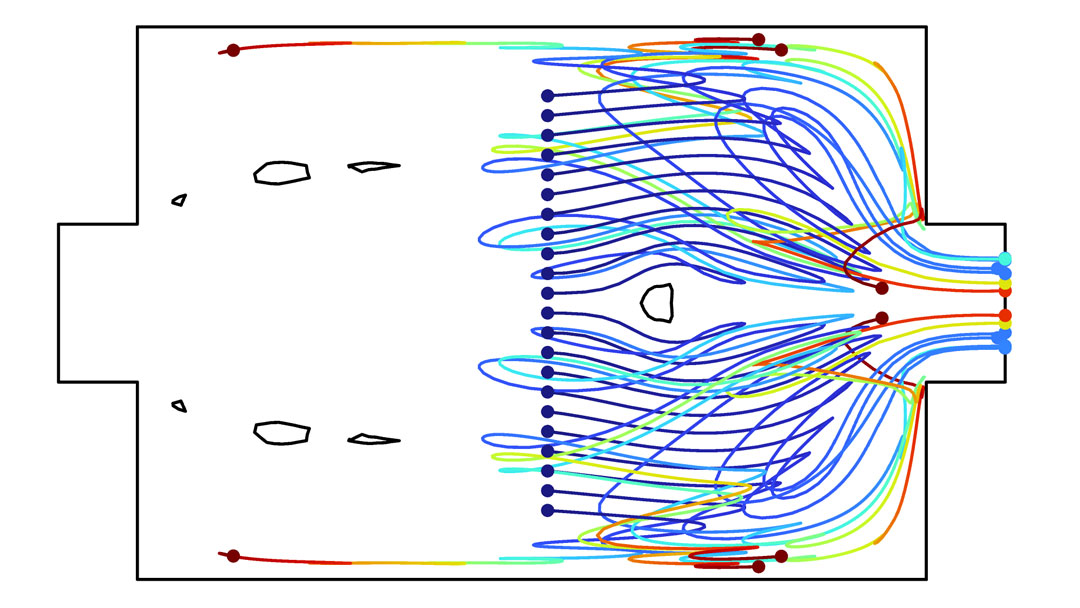
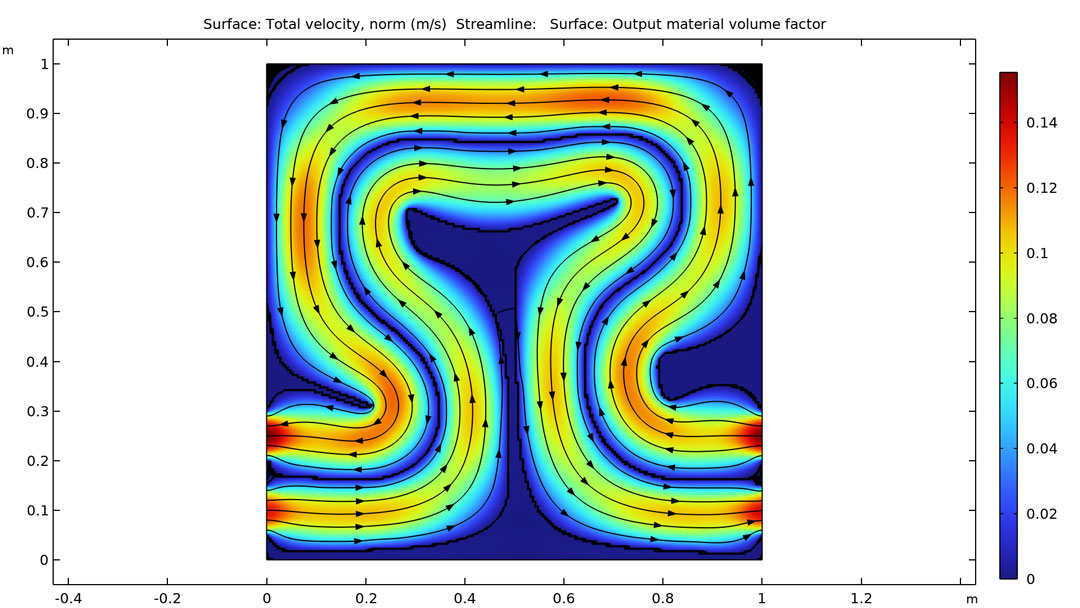
Optimization of a Tesla Microvalve with Transient Flow |
|
Topology Optimization of a Heat Exchanger with Laminar Flow |
Optimal Control for Heating of a Cylinder |
|
Shape Optimization of a Rectangular Loudspeaker Horn in 3D |
Shape Optimization of a Water Heater |
5.6
NOVEDADES
Optimización de parámetros de diseño
Al realizar la optimización de los parámetros de diseño con un resolvedor de optimización sin derivadas, se genera una tabla de objetivos por defecto. Ahora puede hacerse clic con el botón derecho en una fila de dicha tabla y elegir Copiar filas seleccionadas a nuevos casos de parámetros. Esto simplifica el flujo de trabajo cuando desea realizar más análisis sobre el resultado optimizado.
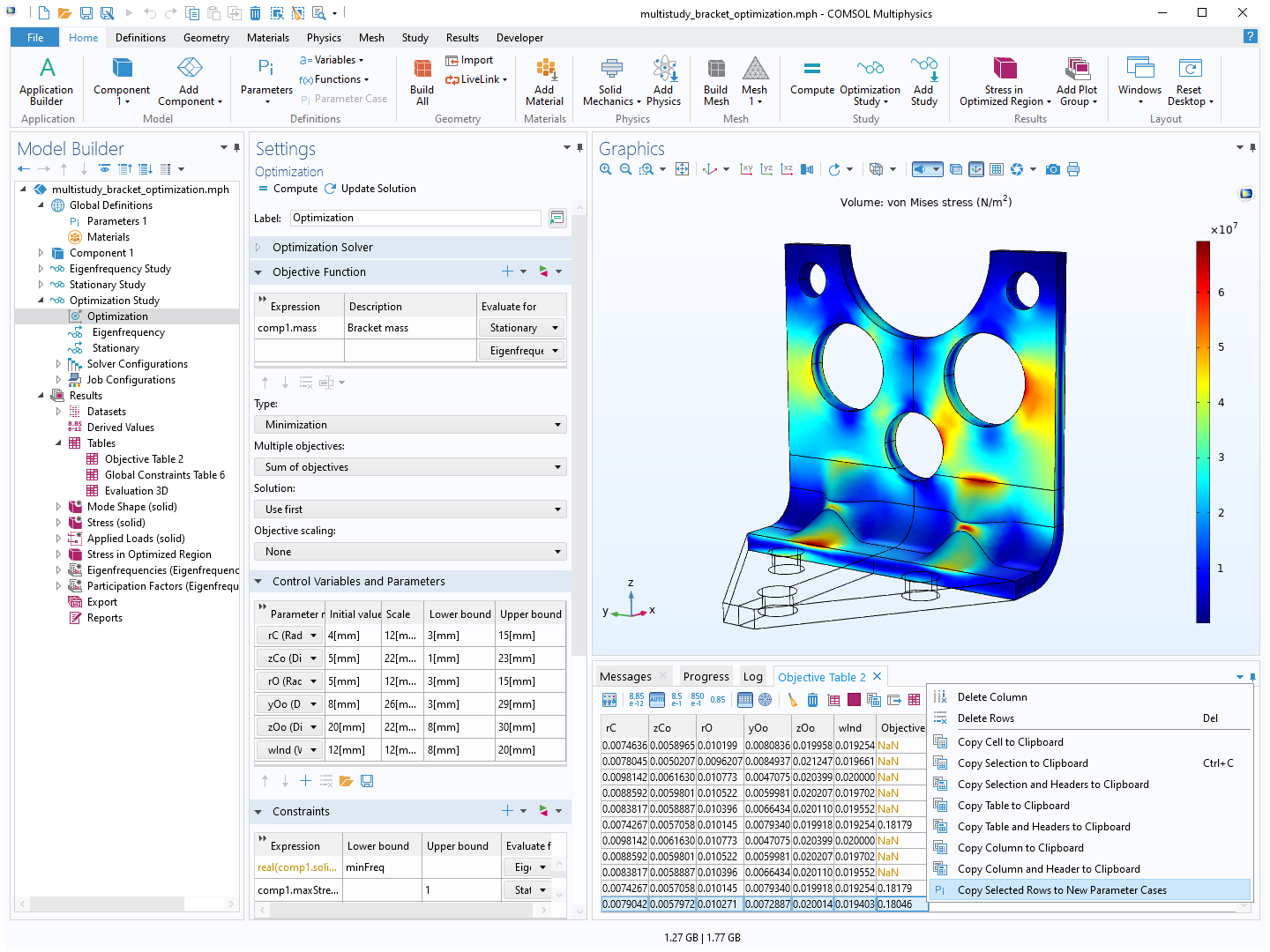
El modelo multistudy_bracket_optimization minimiza la masa de un soporte al tiempo que restringe la frecuencia propia y la tensión máxima. Los valores de parámetro optimizados se pueden copiar a un nuevo caso de parámetro haciendo clic con el botón derecho en la tabla de objetivos.
Optimización de formas
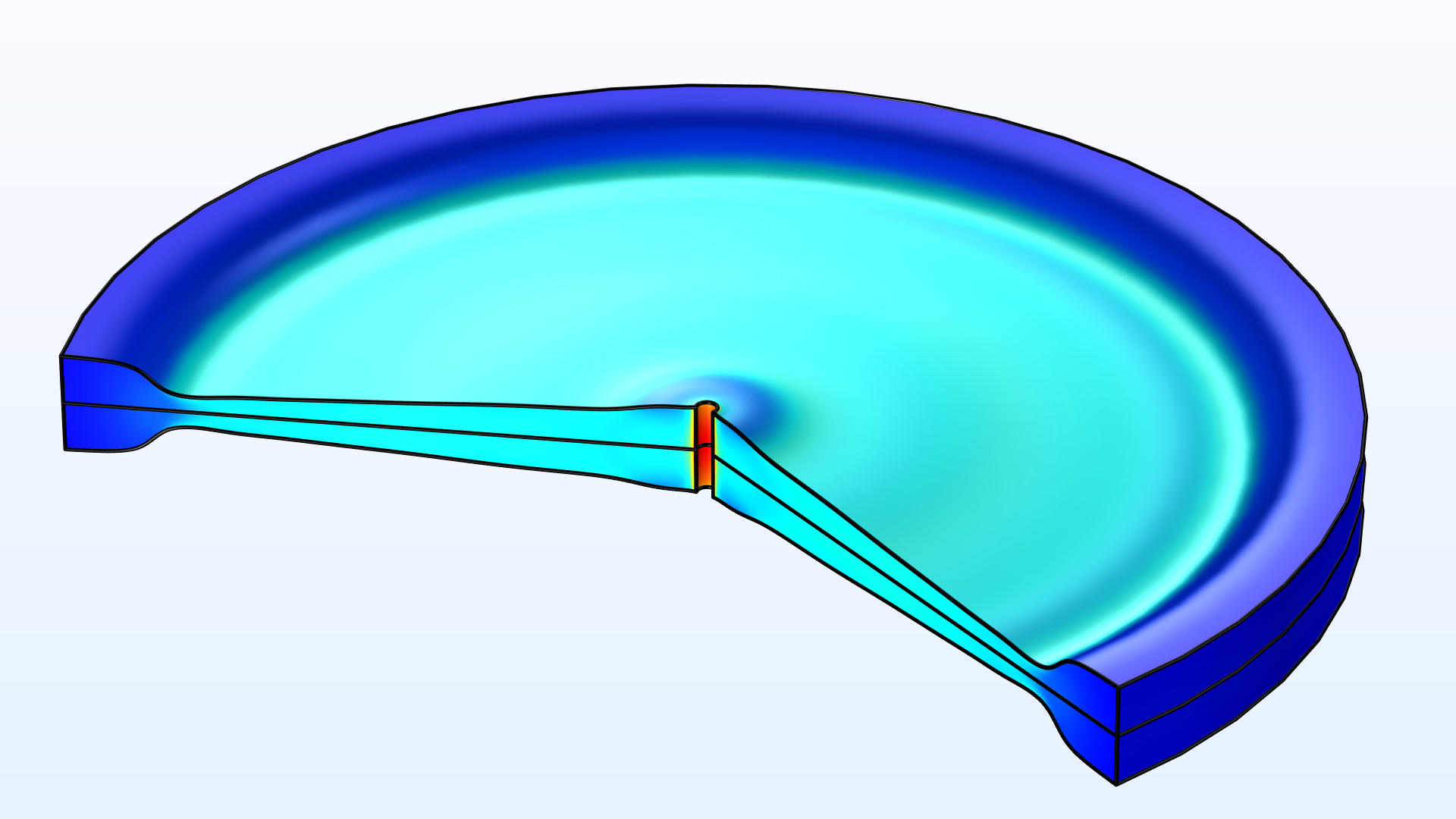
Hay un nuevo paso de estudio de Optimización de forma dedicado a la optimización basada en gradientes. Además, hay un nuevo resolvedor de optimización basado en gradientes, IPOPT, que utiliza un algoritmo de punto interior. Este resolvedor está disponible para todos los estudios de optimización. El resolvedor tiene propiedades similares a SNOPT, pero IPOPT es un proyecto de código abierto en desarrollo activo. El nuevo paso de estudio y el resolvedor de IPOPT se utilizan en varios modelos tutoriales, incluido el modelo "Optimizing a Flywheel Profile". En COMSOL Multiphysics ® versión 5.6, este modelo utiliza un componente de revolución con una interfaz de Mecánica de sólidos junto con las características incluidas para optimización de forma.
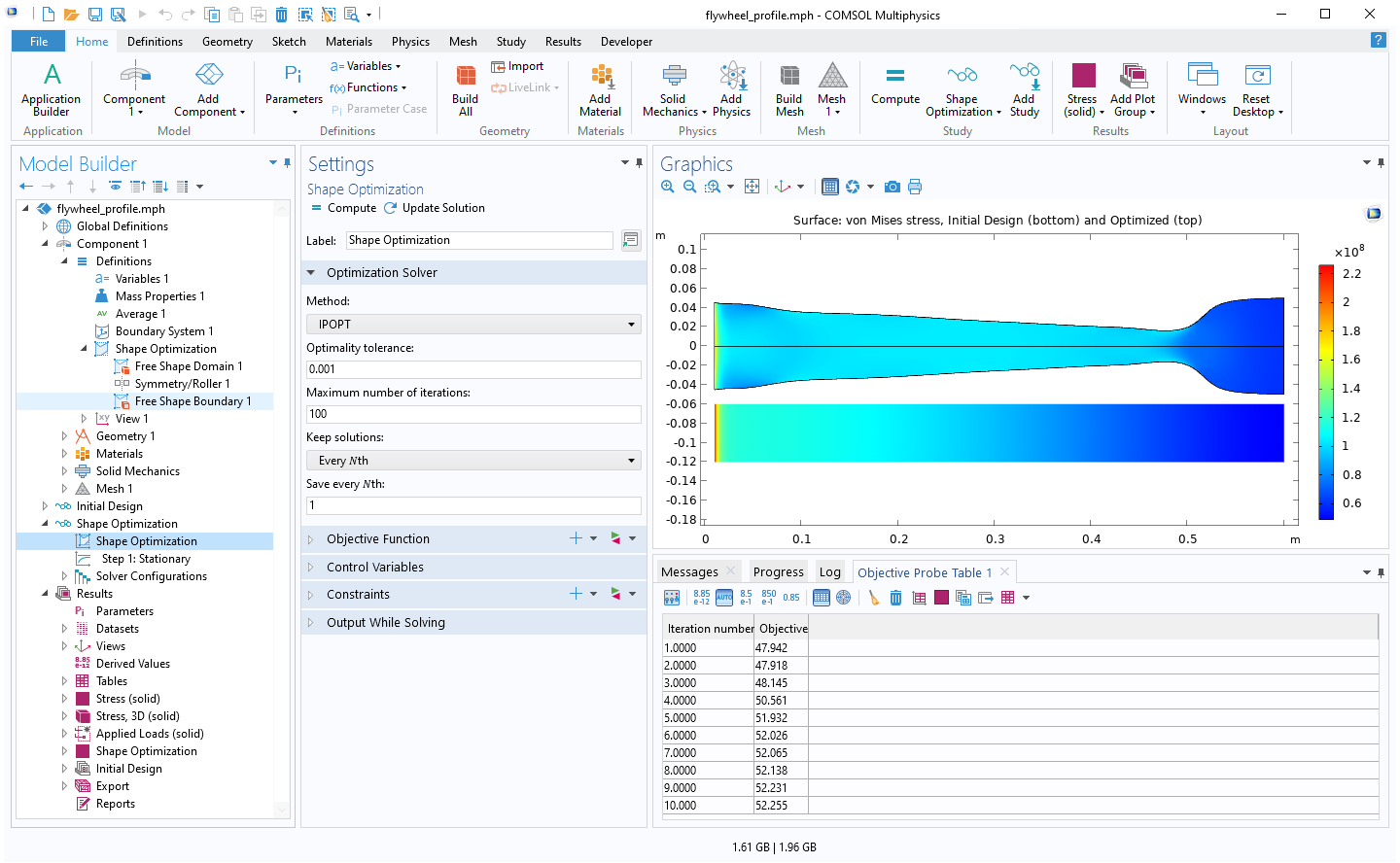
El resolvedor de optimización IPOPT se combina con la función Límite de forma libre para aumentar el momento de inercia de un volante sin aumentar la masa o la tensión máxima de von Mises (aproximada).
Optimización de topología
Existe un nuevo paso de estudio Optimización de topología dedicado a la optimización basada en el gradiente que soporta el nuevo resolvedor de optimización IPOPT. Además, se dispone de una nueva opción para Mantener soluciones que permite guardar varias soluciones de optimización intermedias. Se puede escoger entre guardar el Último N o Cada N solución. La opción es útil para encontrar errores en el modelo así como para crear animaciones del progreso de optimización.
Muchos resolvedores de optimización trabajan mejor si la función objetivo está bien escalada, y los pasos de estudio ahora disponen de una opción llamada Escala de objetivo, que puede utilizarse para configurar una escala manual o una escala basada en la solución inicial. Esto simplifica la configuración de muchos problemas de optimización de topología. Un nuevo material Enlace de topología y una herramienta de ayudante de modelado configuran automáticamente el caso común de minimización de cumplimiento de las restricciones de volumen para la optimización de la topología estructural.
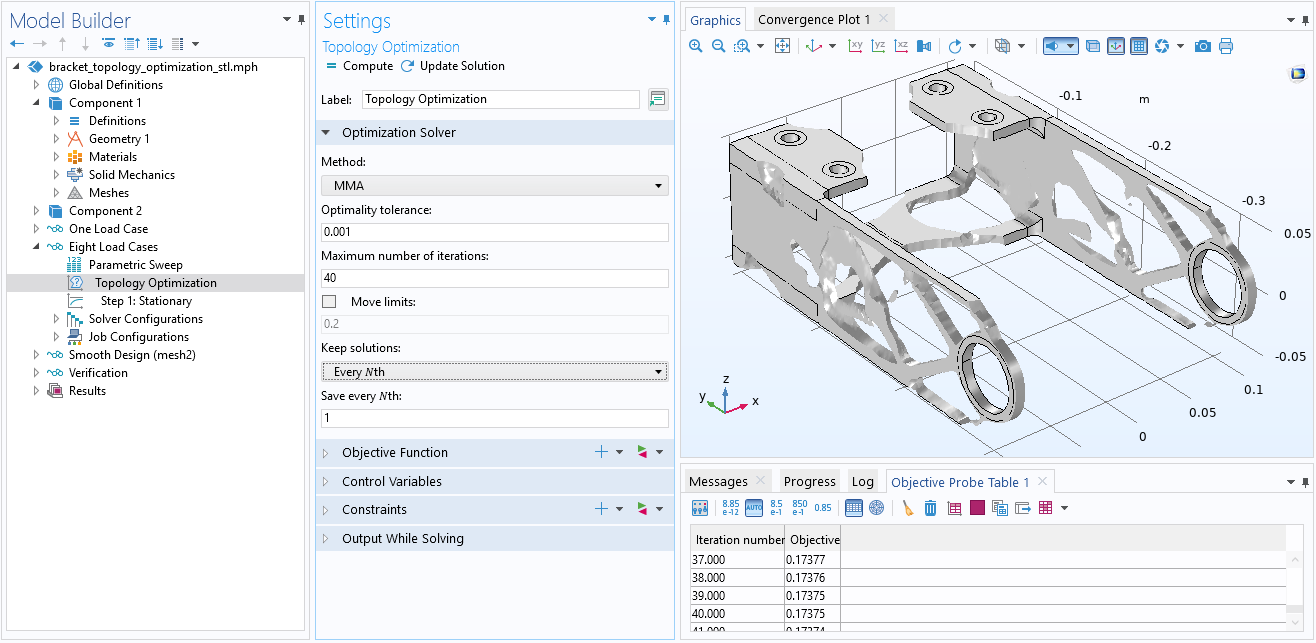
La soluciones Mantener soluciones, se pueden configurar para guardar todas las N soluciones. Si N = 1, todas las soluciones se guardarán y luego podrá inspeccionarse el progreso de la optimización en detalle.
Nuevos modelos tutoriales
|
Optimizing a Flywheel Profile |
Optimization of a Photonic Crystal for Signal Filtering |
|
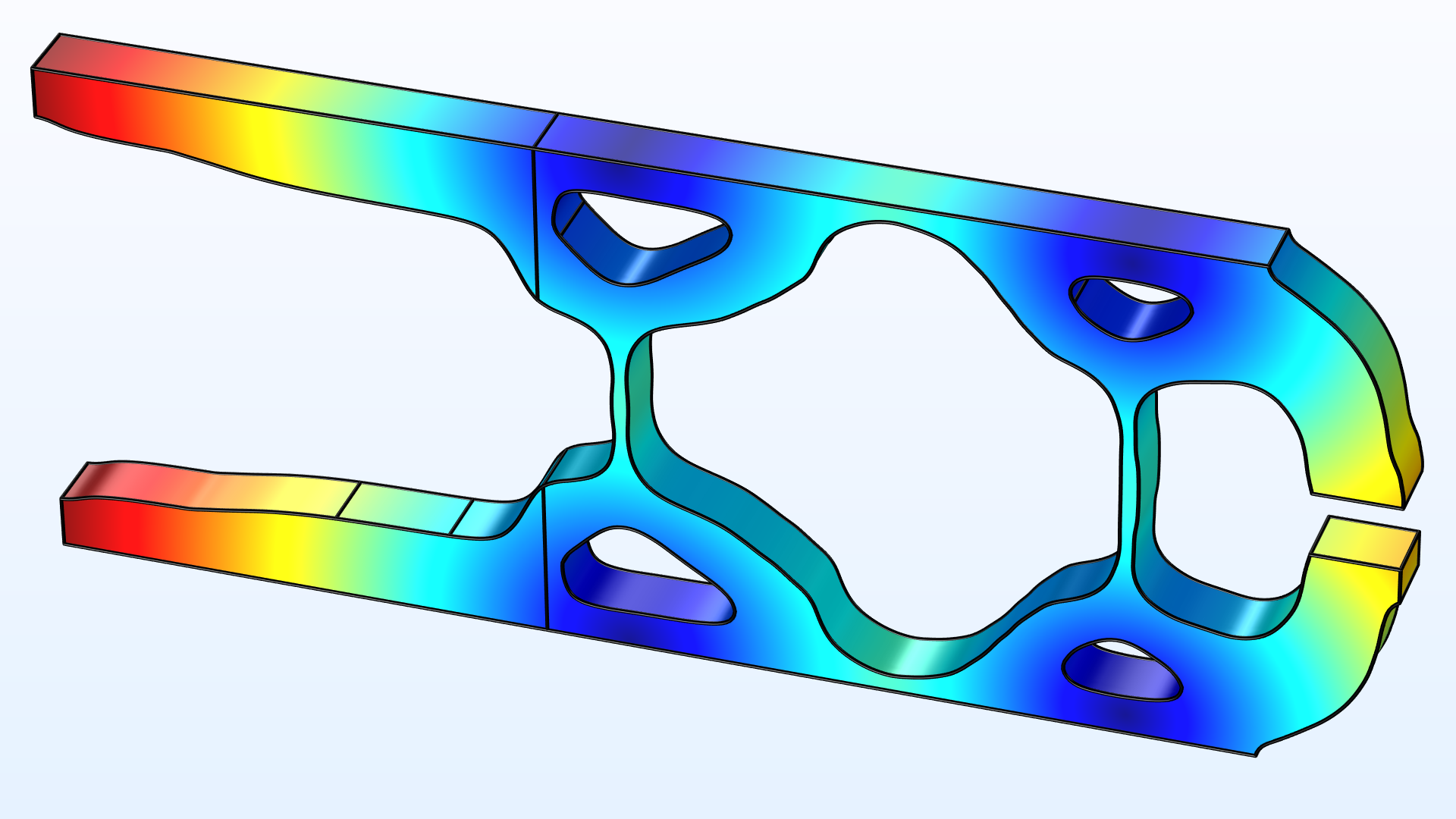
Shape and Topology Optimization of Compliant Pliers |
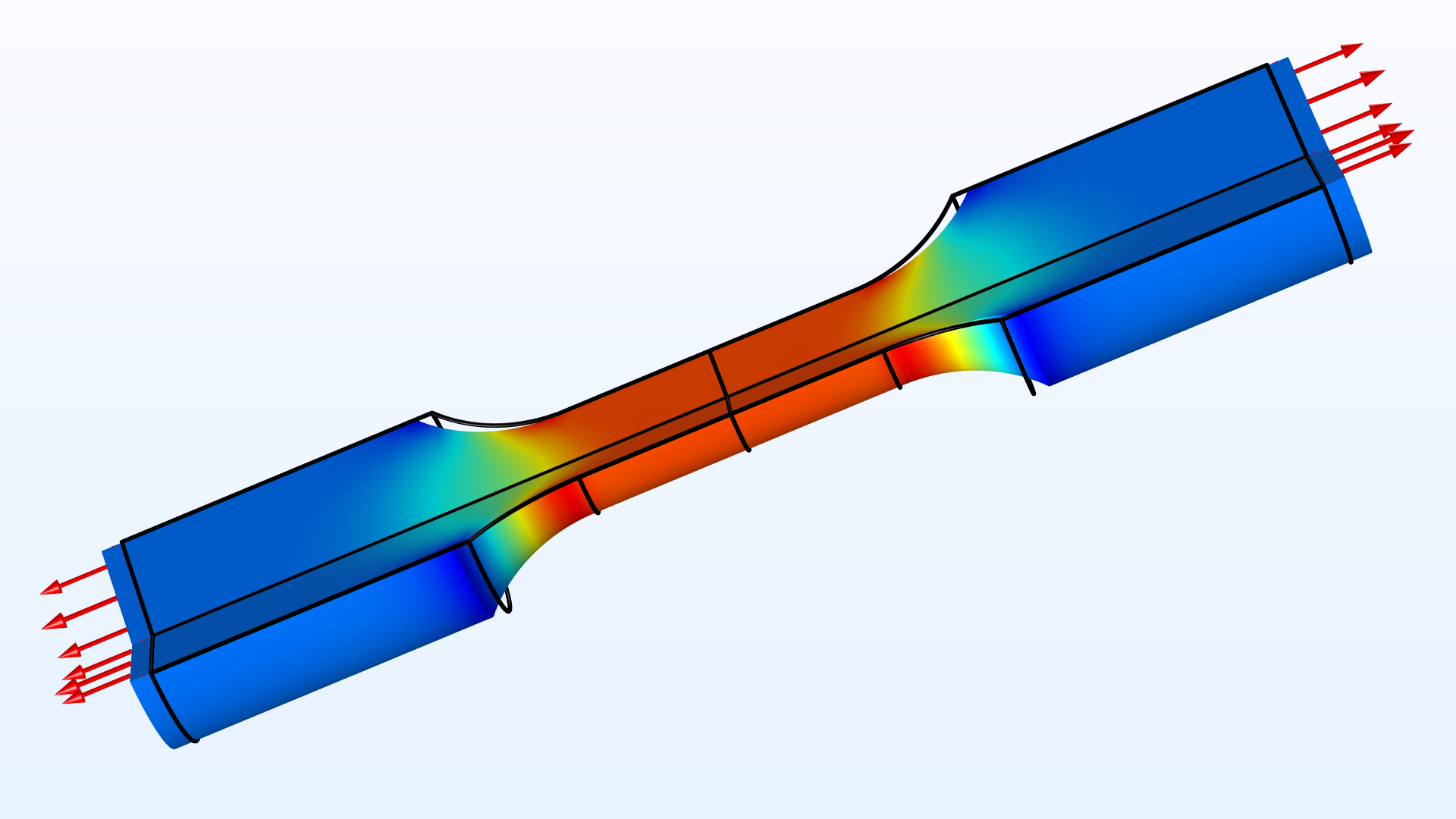
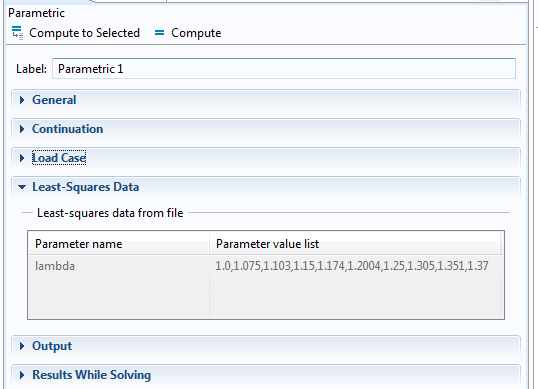
Parameter Estimation for a Tensile Test |
|
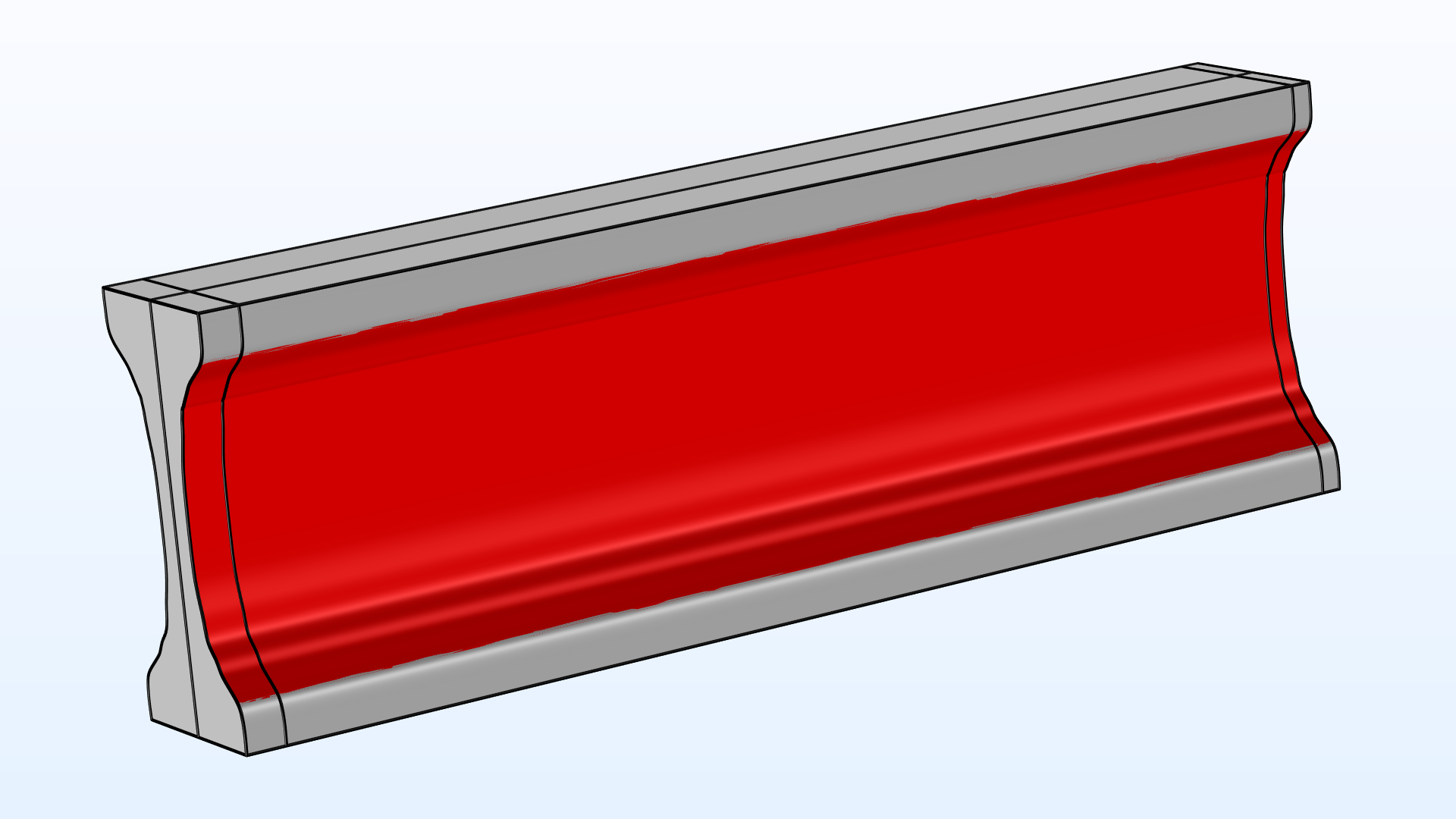
Shape and Topology Optimization of an Extruded Beam |
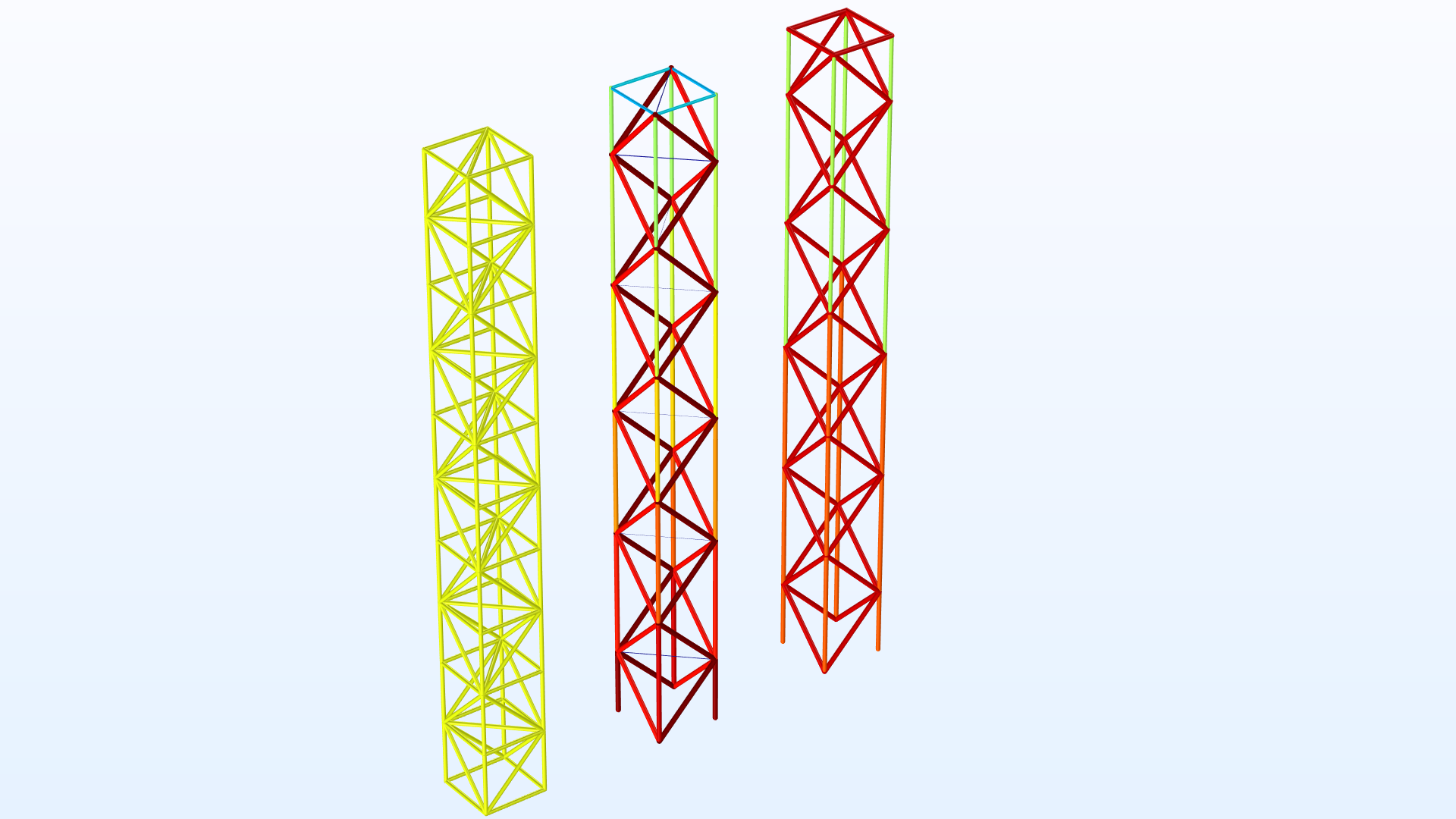
Optimization of a Truss Tower |
5.5
NOVEDADES
La versión 5.5 incluye una configuración simplificada de optimización de forma con nuevas funcionalidades incluidas, un conjunto de datos de filtros para suavizar los resultados de optimización de topología y aplicación estricta de las restricciones de diseño para optimización sin derivadas.
Optimización de forma
Configurar problemas de optimización de forma ahora es más fácil. A partir de la versión 5.5 se pueden seleccionar partes de una geometría para optimización de forma utilizando la nueva funcionalidad Free Shape Domain. Los contornos a ser optimizados se especifican utilizando las funcionalidades Polynomial Boundary o Free Shape Boundary, que tienen soporte interno para la regularización. Ahora también se puede realizar optimización de forma sobre conchas utilizando la nueva funcionalidad Free Shape Shell. La funcionalidad Symmetry/Roller especifica puntos o aristas que pueden deslizarse sobre un contorno plano. Todas las funcionalidades interactúan con las demás para asegurar continuidad, y el gráfico por defecto facilita visualizar el resultado.
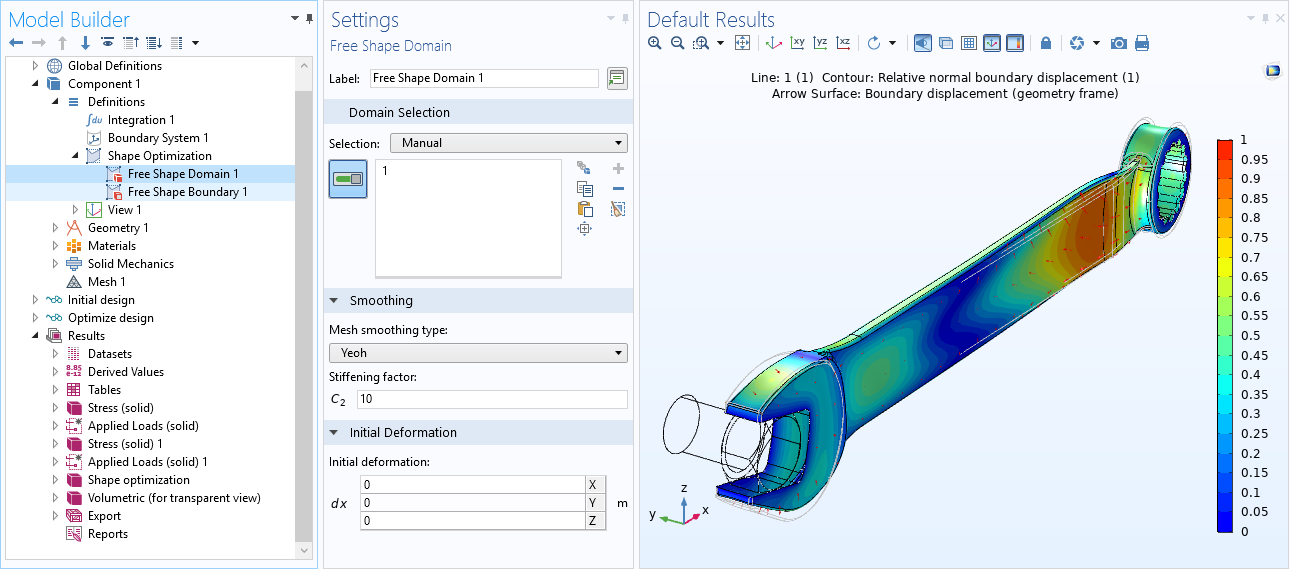
La nueva ventana de ajustes de la funcionalidad de optimización de forma Free Shape Domain disponible bajo las definiciones del componente.
Optimización de topología
El gráfico por defecto para optimización de topología 3D ahora utiliza el nuevo conjunto de datos Filter, del que se puede crear directamente una parte de malla. De esa manera, la geometría optimizada puede ser importada en un nuevo componente mantenientod todas las selecciones asociadas con la geometría de optimización de topología. Esto reduce el trabajo necesario para configurar una simulación de verificación de un resultado de optimización de topología. Una nueva funcionalidad Prescribed Density interactúa con la funcionalidad Density Model, mejorando el comportamiento del filtro de regularización cerca de los contornos. Esto puede mejorar la robustez cuando se crea una parte mallada basada en el campo filtrado.
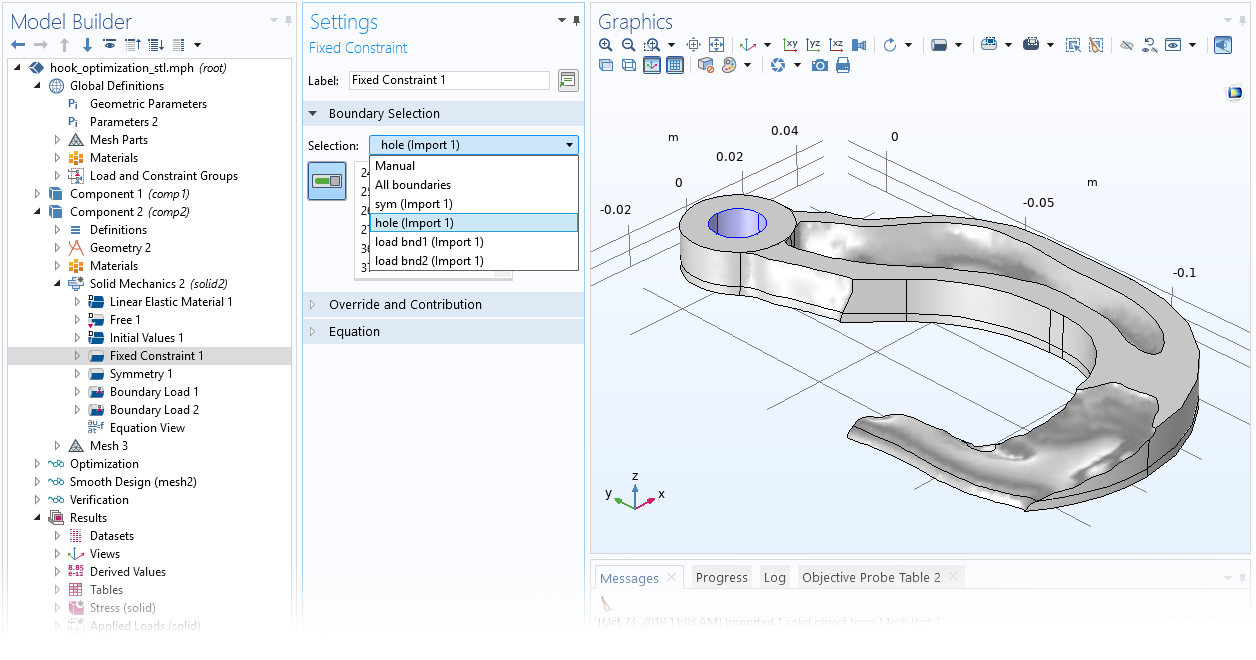
Las selecciones del viejo componente pueden reciclarse cuando la geometría se importa desde una parte mallada apuntando a un conjunto de datos Filter.
Estimación de parámetros
Cuando se resuelve un estudio de estimación de parámetro con el método de Levenberg-Marquardt se puede calcular los intervalos de confianza para los parámetros basándose en un nivel de confianza definido por el usuario. El cálculo de los intervalos considera que las medidas son independientes y que el error está normalmente distribuido. Entonces se podría combinar los intervalos de confianza con la generación de datos sintéticos para estimar el tamaño de muestra requerido para obtener una cierta precisión para los parámetros.
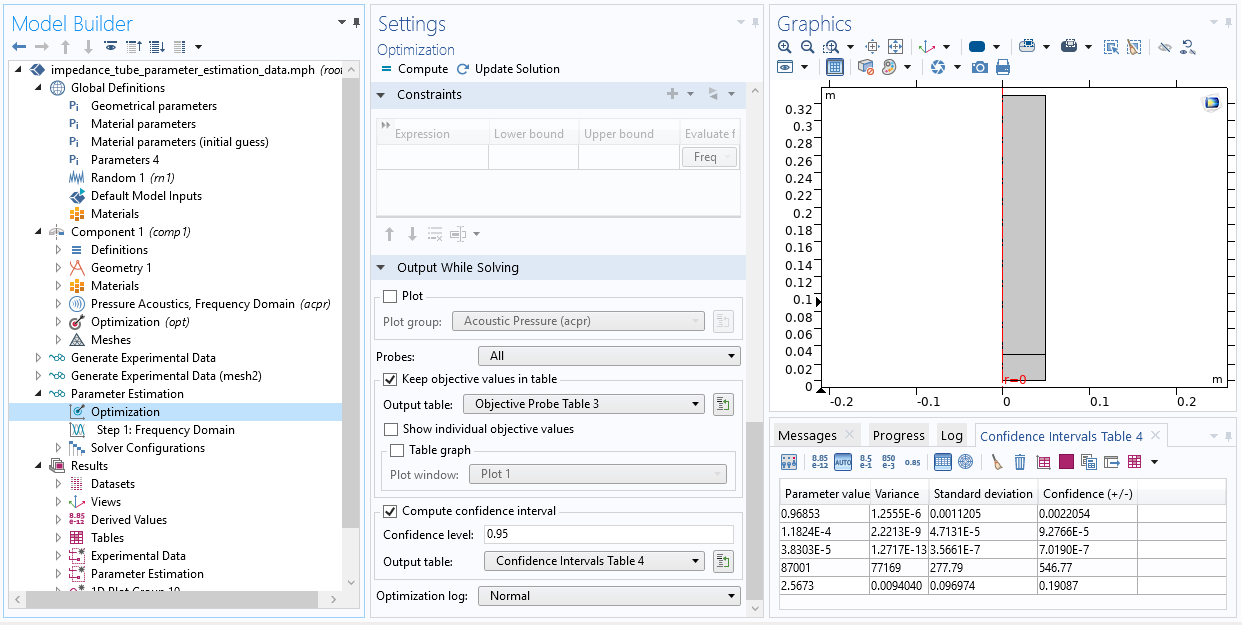
El cálculo de intervalos de confianza en la estimación de parámetros puede habilitarse en el paso de estudio Optimization.
Optimización de parámetros
Los resolvedores libres de derivadas ahora tienen una opción para la aplicación estricta de las restricciones de diseño, mejorando la robustez y reduciendo el tiempo computacional. El modelo no será evaluado para controlar conjuntos de parámetros que violen restricciones dependiendo únicamente de los parámetros de control. La opción está habilitada por defecto para COBYLA y Nelder–Mead. Puede verse esta funcionalidad en el modelo multistudy_bracket_optimization.
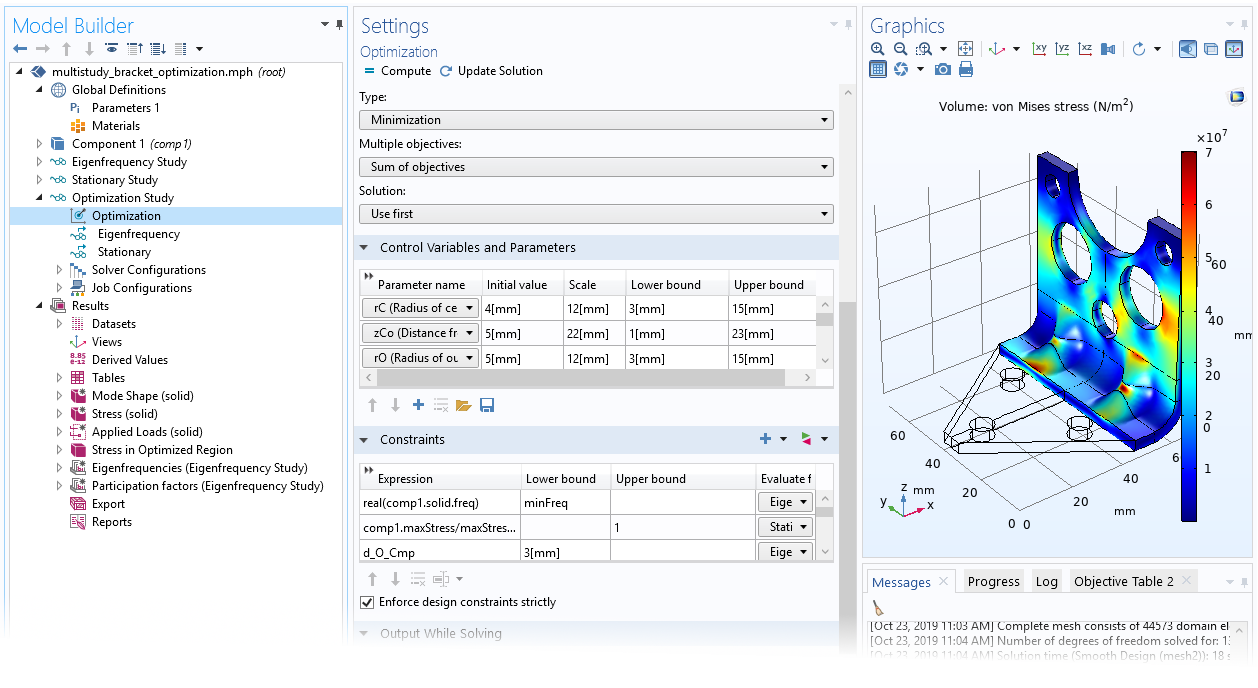
La optimización de parámetros ahora a menudo puede ser realizada de forma más robusta definiendo restricciones de diseño que prevengan cambios topológicos. La aplicación estricta de las restricciones de diseño puede mejorar el comportamiento de estos modelos.
5.4
NOVEDADES
Optimización de la topología utilizando filtrado de Helmholtz
La capacidad para optimizar topologías se ha mejorado con el soporte de filtrado, proyección e interpolación de Helmholtz, Una nueva funcionalidad Density Model disponible bajo Definitions>Topology Optimization en los componentes del modelo proporciona ajustes para añadir filtrado, proyección e interpolación.
Barridos paramétricos y optimización libre de derivadas
Ahora es posible añadir un paso de estudio Parametric Sweep sobre un paso de estudio Optimization y viceversa si el estudio Optimization utiliza un método libre de derivadas (Nelder-Mead, Monte Carlo, BOBYQA, COBYLA, búsqueda de Coordenadas). Solo puede existir un paso de estudio Optimization, pero están permitidos más pasos de estudio Parametric Sweep.
Otras mejoras
- La casilla Keep objective values in table ahora está disponible para los métodos de optimización Levenberg-Marquardt y MMA con objetivos de mínimos cuadrados. Por defecto está habilitada. Esto significa que se creará una tabla de objetivos mientras se corre. En consecuencia, La compatibilidad hacia atrás de la API puede perderse en algunos casos. Los usuarios de la API necesitan actualizar el código que intenta acceder o hacer construir alguna tabla específica después de que la optimización haya corrido. La tabla podría ya haber sido utilizada por el resolvedor de optimización.
Cuando la fuente de datos es Result table o Local table, también se pueden seleccionar ítems en la Data column limpiando o seleccionando la correspondiente casilla en la columna Use. Entonces se puede, por ejemplo, utilizar la misma tabla de resultados para contener los datos de entrada y salida experimentales cuando se realiza una optimización dependiente del tiempo utilizando una carga dependiente del tiempo. - Se ha añadido visualización de la ecuación en la interfaz Optimization.
- Mejora de estabilidad en Windows® 10.
5.2
Problemas de optimización LSQ mejorados
5.0
Optimización multianálisis
Nuevas herramientas para crear referencias de estudio que permiten la optimización multianálisis utilizando combinaciones de estudios de optimización.
Soporte para parada y continuación
Cuando se para cualquier resolvedor de optimización ahora existe la opción de continuar.
Nuevo paso de estudio de estimación de parámetros
Un nuevo paso de estimación de parámetro simplifica la estimación básica de parámetros y la obtención del objetivo.
Mejoras y nuevos métodos de optimización
Un nuevo método libre de derivada, Optimización con restricción por aproximación lineal, (COBYLA), está disponible, así como resolvedores de optimización mejorados. Es un método iterativo para optimización con restricciones libre de derivada. Cada iteración forma aproximaciones lineales al objetivo y funciones de restricción por interpolación en los vértices de un simplex y un límite de región de confianza restringe cada cambio de las variables.
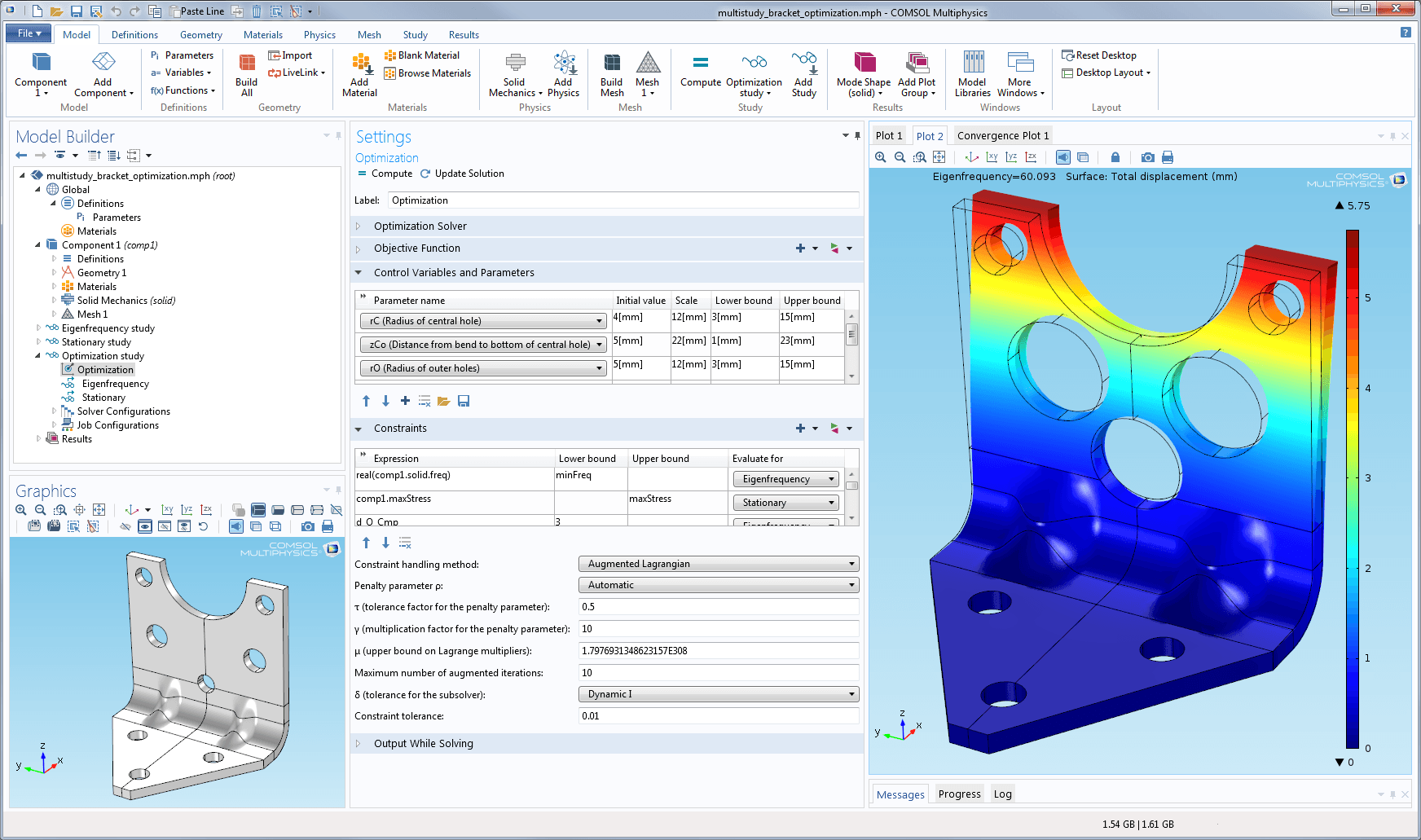
Optimización multianálisis: Simulación de un soporte utilizado para montar componentes pesados en sistemas vibrantes. Los resultados muestran la deformación e un modo propio en el acero después de optimizar el radio de los agujeros y grosores de las indentaciones para reducir el peso.























 COMSOL Multiphysics 6.4
COMSOL Multiphysics 6.4