En Mark 29.3, NAG presenta un resolvedor de vanguardia (nag_mip_handle_solve_milp) diseñado específicamente para abordar problemas de programación lineal entera mixta (MILP) a gran escala. Esto marca un paso significativo en el compromiso de NAG de mejoar y ampliar sus ofertas en el campo de la optimización matemática.

MILP encuentra una aplicación generalizada en diversas industrias, incluidas, entre otras, la fabricación, la logística, el transporte y las telecomunicaciones. Al acomodar variables de decisión tanto continuas como discretas, el resolvedor permite a las organizaciones modelar problemas prácticos y complejos, incluyendo la asignación de recursos, la programación y el flujo de red.

Problemas MILP a gran escala de la forma

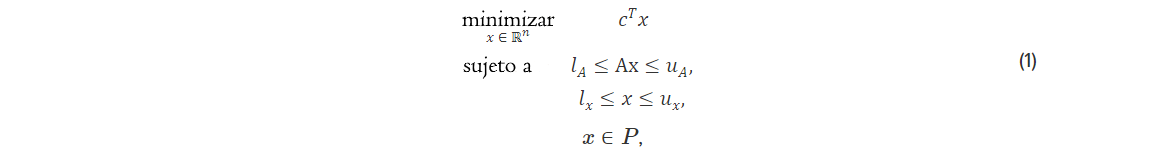
dónde 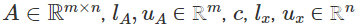son los datos del problema y 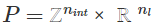son bastante omnipresentes en aplicaciones de la vida real. Es importante resaltar que resolver problemas MILP plantea un desafío considerable debido a su naturaleza combinatoria y, en muchos escenarios prácticos, encontrar una solución exacta en un tiempo razonable puede resultar muy difícil. Nos complace presentar la última incorporación a la librería NAG y nuestro objetivo es ayudar a los usuarios a tomar decisiones de manera eficiente y precisa.

Modelado y resolución MILP

El modelo (1) cubre muchos casos de uso práctico. Una de las características distintivas de MILP es su capacidad para modelar condiciones lógicas como implicaciones o dicotomías.

Tomemos como ejemplo el modelado de carga fija. Las actividades económicas frecuentemente implican costes tanto fijos como variables. En estos casos, un coste fijo f_ix solo ocurre cuando variable y es positiva. Dado un coste variable c_var, el coste total cuando y>0 es c_fix+c_vary y 0 en caso contrario. Es fácil observar que la función de costes no es lineal. Introduciendo una variable binaria x podemos modelarlo como la expresión lineal

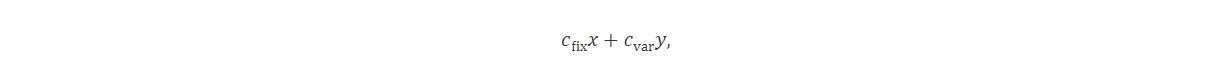
Donde añadimos restricciones

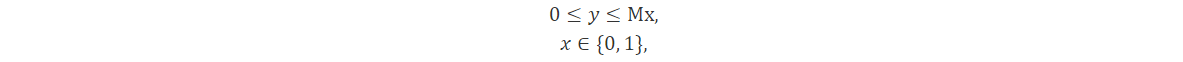
Donde M es un límite superior de y y debe elegirse como el límite más estricto conocido, en lugar de un límite arbitrariamente grande M. Esta técnica de modelado aparece en aplicaciones como la ubicación de instalaciones y el diseño de redes.

Otro gran uso de MILP es modelar disyunciones. Por ejemplo, al programar trabajos en una máquina, es posible que deseemos permitir el trabajo i para ser programado antes del trabjo j o viceversa. Consideremos que p_i y p_j denotan el tiempo de procesamiento del trabajo i y j, mientras que t_i y t_j representan sus tiempos de inicio. Entonces requeriremos que se cumpla al menos una de las siguiente restricciones.

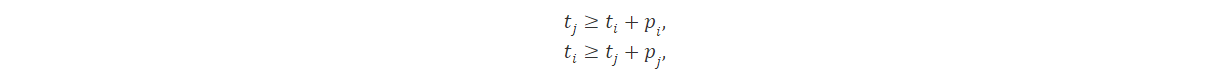
Introduciendo variables binarias x₁ y x₂ el problema se puede modelar como

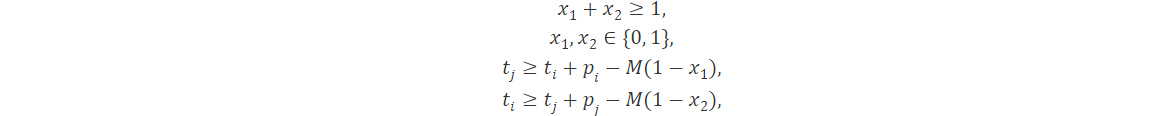
donde M nuevamente es positivo y sirve como límite conocido.

Hay muchos otros tipos de restricciones que son muy útiles en el campo de la investigación de operaciones, incluidas, entre otras,

• Variables semicontinuas donde una variable x es 0 o está en un intervalos [a,b],
• variables que solo toman valores de un conjunto, por ejemplo ,
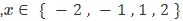• funciones lineales continuas por partes, que pueden verse como una combinación de funciones lineales.

Consulte [1,2] para conocer más técnicas de formulación y su uso en la programación.

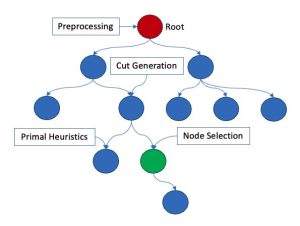
Figura 1: Ilustración de un árbol de ramificación y acotamiento

Para resolver (1) de manera eficiente, el algoritmo de ramificación y acotamiento sirve como marco fundamental, que está equipado con técnicas MILP modernas como preprocesamiento, generación de cortes y diversas heurísticas. En la Figura 1 se muestra una parte de un árbol de ramificación y acotamiento. A partir del problema original, denominado nodo raíz, el algoritmo genera varios nodos secundarios dando forma a la región factible mediante la adición de más restricciones, como el corte fraccional de Gomory. Cada nodo se resuelve como una programación lineal continua mediante un método simplex dual eficiente. Se adoptan varias heurísticas para obtener un mejor límite inferior. Al poder con éxito el árbol de búsqueda y seleccionar los nodos de búsqueda, aumenta en gran medida la posibilidad de que un algoritmo de ramificación y enlace encuentre la solución óptima en un tiempo razonable. Consulte [3] para obtener más detalles sobre algortimos para resolver MILP.

El resolvedor MILP nag_mip_handle_solve_milp está completamente integrado en NAG Optimization Modelling Suite, que permite a los usuarios expresar mejor los problemas del mundo real en el modelo matemático, mejorando la comprensión del funcionamiento interno del modelo. Durante el proceso de modelado, los usuarios pueden

• ver el efecto de una restricción o variable particular eliminándolas temporalmente y luego recuperándolas;
• modificar coeficientes individuales del objetivo lineal o de las restricciones lineales;
• fijar una variable a una constante dada, lo que da como resultado la eliminación de una variable en toda la formulación y la disminución de la dimensión del problema.

El resolvedor está disponible para múltiples lenguajes y entornos, incluyendo C y C++, Python, Java, .NET y Fortran, en Windows, Linux y MacOS.

Referencias

[1] Vielma JP. Mixed integer linear programming formulation techniques. Siam Review. 2015;57(1):3-57.
[2] Floudas CA, Lin X. Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Annals of Operations Research. 2005 Oct;139:131-62.
[3] Conforti M, Cornuéjols G, Zambelli G, Conforti M, Cornuéjols G, Zambelli G. Integer programming models. Springer International Publishing; 2014.