Predecir tendencias a corto plazo con análisis de tendencias: dejar de hacer conjeturas y empezar a pronosticar
- Detalles
- Categoría: Minitab
- Visto: 1479

Por Joshua Zable
Como Director Financiero, siempre me enfrento al reto de equilibrar decisiones a corto y largo plazo. Comprender las perspectivas a corto plazo me permite acelerar o frenar adecuadamente las inversiones a largo plazo sin comprometer los resultados a corto plazo. Demasiados ejecutivos estiman la tendencia a corto plazo basándose en su intuición o experiencia, sobre todo cuando existe un método de series de tiempo muy sencillo, apropiadamente llamado Análisis de Tendencias , que nos ofrece una visión estadística del corto plazo. Así es como Minitab puede ayudarle a realizar pronósticos fiables a corto plazo en minutos (¡o menos!).
Análisis de tendencias: su método de pronóstico a corto plazo
Para ser claros, existen muchos métodos estadísticos potentes que pueden utilizarse para pronosticar. El análisis de tendencias se prefiere a corto plazo debido a su simplicidad y la capacidad de configurar y ejecutar un modelo rápidamente. Otros métodos, como ARIMA u otros métodos de aprendizaje automático, son bastante potentes, pero su configuración o ejecución pueden requerir más tiempo.
Ver la tendencia e identificarla antes de pronosticar
Aunque el análisis de tendencias es simple, como la mayoría de los métodos estadísticos, requiere cierta reflexión. En este caso, la forma o pendiente de la tendencia será crucial para el análisis. Representar gráficamente los datos debería dar una pista visual sobre qué modelo de análisis de tendencias utilizar. Sin embargo, a veces las formas pueden parecer similares, por lo que comprender mejor los escenarios típicos descritos por estos modelos le ayudará a decidir. Si aún no se siente seguro, puede ejecutar cada modelo en su conjunto de datos y medir su ajuste utilizando medidas de precisión como MAPE, MAD y MSD . Medir el ajuste de cada modelo puede ser un proceso minucioso, pero también puede requerir mucho tiempo.
Para visualizar su tendencia, utilice el software estadístico Minitab y acceda a nuestro popular Constructor de gráficos. Seleccione "Gráfico de series de tiempo" o vaya al menú Estadísticas > Series de tiempo > "Gráfico de series de tiempo" y grafique sus datos. Una vez que tenga el gráfico, su modelo probablemente se parecerá a uno de los tipos de modelo más comunes: lineal, cuadrático, de crecimiento exponencial y logístico de curva S/Pearl-Reed.
A continuación se muestran ejemplos de gráficos de series temporales de los tipos de tendencias que están asociados con los diferentes tipos de modelos.
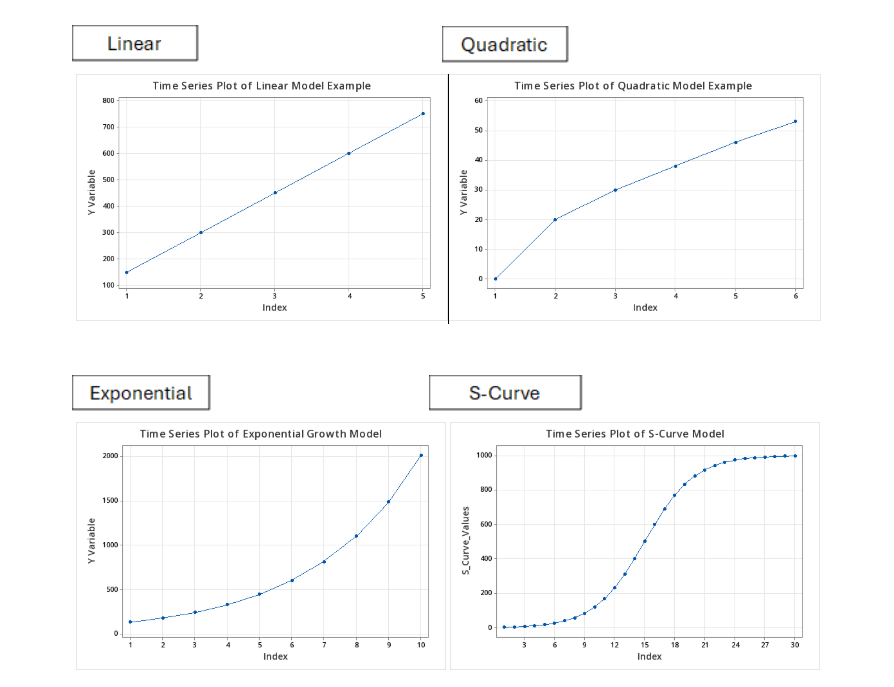
Comprensión de los modelos lineales: Los modelos lineales son líneas rectas (para quienes tengan inclinación por las matemáticas, se representan mediante la ecuación Y = a + bX). En la práctica, los modelos lineales representan tendencias con tasas constantes o fijas. En el sector manufacturero, esto podría ser una simple tasa de producción (es decir, cuánto produce una máquina por hora), la tasa de consumo de energía o los costos (suponiendo que no haya ahorros de costos a escala). En cuanto a la previsión de ventas, el modelo lineal se utiliza cuando se espera una tasa de crecimiento similar .
Modelos cuadráticos: ¿una sonrisa o un ceño fruncido?
A diferencia de los modelos lineales, los modelos cuadráticos reflejan una tasa de cambio no constante. Pueden reflejar una tendencia de aceleración o desaceleración y, por lo tanto, confundirse con un modelo exponencial (¡por eso también es tan importante comprender los datos!). Un ejemplo común de manufactura cuadrática podría ser modelar la producción en función de la mano de obra. En algún momento, añadir demasiados trabajadores o aumentar sus horas de trabajo genera rendimientos decrecientes. Otro ejemplo común es modelar precios y ganancias. Si bien el aumento de precios incrementa las ganancias, con el tiempo, un precio más alto podría obstaculizar la demanda, perjudicándola y ralentizando el crecimiento incremental de las ganancias.
Crecimiento exponencial: Ya sea que se encuentre en una situación de crecimiento constante o experimentando una caída exponencial, este modelo significa que la tasa de cambio no solo se acelera o desacelera (como en los modelos cuadráticos), sino que cambia más rápido que en los modelos cuadráticos. Este tipo de modelo se puede utilizar en diversas disciplinas. En finanzas, puede usarse para modelar el interés compuesto, mientras que en ciencias podría modelar la propagación de una pandemia o la propagación de bacterias en un experimento. El crecimiento exponencial también puede observarse en el lanzamiento de un nuevo producto o fármaco, a medida que la adopción se acelera con la concienciación y la aceptación.
Distinguir el crecimiento cuadrático del exponencial es probablemente lo más complicado, por lo que comprender la situación de los datos es crucial. Como mencioné antes, en caso de duda, compare los modelos cuadrático y exponencial midiendo el ajuste con medidas de precisión como MAPE, MAD y MSD .
Curva S/Logística Pearl-Reed: La curva S, a menudo denominada curva logística Pearl-Reed, fue formalizada por primera vez en 1920 por Raymond Pearl y Lowell J. Reed, dos biólogos estadounidenses. Introdujeron esta función logística para describir el crecimiento poblacional bajo restricciones como la escasez de recursos. Básicamente, a medida que los recursos escasean, el crecimiento poblacional se desacelera y se estabiliza. Fuera del ámbito de la biología, la curva S se asocia típicamente con la adopción de productos o tecnología. También puede representar capacitación (una vez capacitada, las habilidades se estabilizan) o incluso la fidelización de los clientes. En general, refleja un escenario con margen de crecimiento, pero que finalmente alcanzará la saturación y, para fines de pronóstico, se utiliza típicamente cuando el pronosticador reconoce que la saturación está comenzando a ocurrir.
¡ Listo para pronosticar! Un tutorial rápido de Minitab
Una vez identificado el tipo de modelo, pronosticar es pan comido. Con los mismos datos que usó para trazar su tendencia, vaya a Estadísticas/ Series temporales/ Análisis de tendencias. Aparecerá un cuadro de diálogo que le preguntará qué variable desea pronosticar.
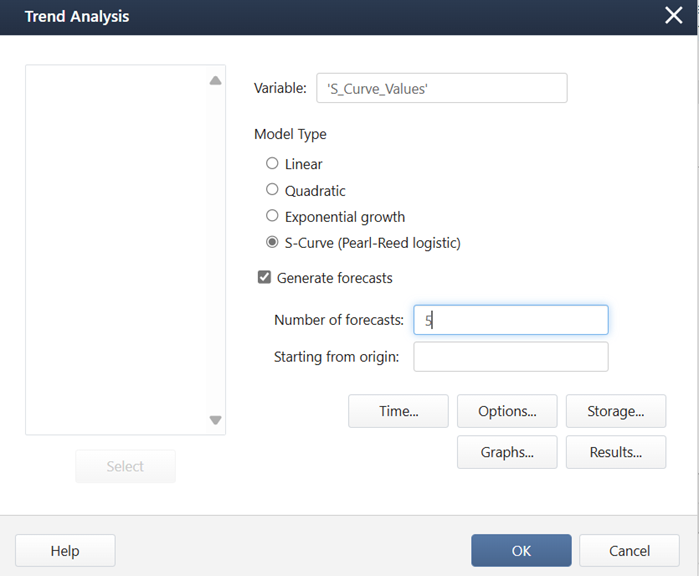
Una vez seleccionada la variable, simplemente seleccione el tipo de modelo y marque la opción "Generar pronósticos". En este ejemplo, quiero generar 5 puntos de datos más, así que escribí "5" en el campo "Número de pronósticos".
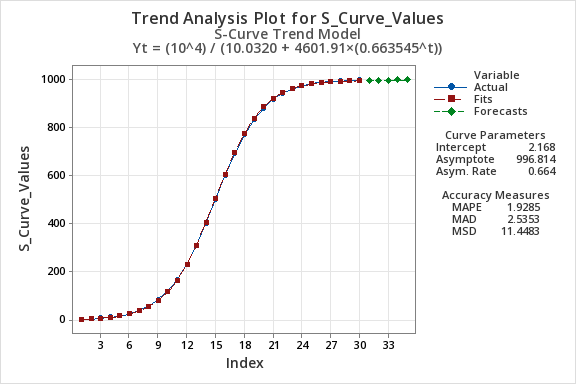
Lea sus resultados…
Tus resultados te proporcionarán una ecuación para tu pronóstico, medidas de precisión, puntos de datos pronosticados y un gráfico. ¡Listo! Misión de pronóstico cumplida.
Ecuación de tendencia ajustada
| Yt = (10^4) / (10.0320 + 4601.91×(0.663545^t)) |
Medidas de precisión
| MAPE | 1.9285 |
| MAD | 2.5353 |
| MSD | 11.4483 |
Pronósticos
| Period | Forecast |
| 31 | 995.441 |
| 32 | 995.902 |
| 33 | 995.209 |
| 34 | 995.412 |
| 35 | 995.547 |
…Y deje que Minitab AI le brinde la confianza para explicarlos
Muchos de los responsables de la previsión no somos necesariamente expertos en estadística. Si bien ya domina el arte de la previsión a corto plazo, proporcionar contexto adicional le dará mayor confianza en sus predicciones. Al usar Minitab AI para generar un resumen en lenguaje natural, puede comprender rápidamente toda la valiosa información que ofrece Minitab. En nuestro ejemplo, el contenido generado por IA explica que el conjunto de datos es lo suficientemente grande como para realizar una predicción precisa y que el modelo generado es fiable.
MINITAB IA
RESUMEN DEL ANÁLISIS ESTADÍSTICO
PROPÓSITO
El análisis busca evaluar la tendencia de los valores de la curva S durante un período específico mediante un modelo de tendencia de curva S. Proporciona información sobre el comportamiento futuro de los datos basándose en la ecuación de tendencia ajustada.
Hallazgos clave
- Ecuación de tendencia ajustada: el modelo predice S_Curve_Values utilizando la ecuación ( Yt = \frac{10^4}{10.0320 + 4601.91 \times (0.663545^t)} ), lo que indica una tendencia decreciente a medida que avanza el tiempo.
- Valores Pronosticados: Los pronósticos para los próximos cinco períodos (31 a 35) muestran valores que aumentarán gradualmente de 995.441 a 996.547, lo que sugiere una estabilización en los Valores de la Curva S.
- Medidas de precisión: El modelo demuestra una buena precisión con un error porcentual absoluto medio (MAPE) de 1,9285, una desviación absoluta media (MAD) de 2,5353 y una desviación cuadrática media (MSD) de 11,4483, lo que indica predicciones confiables.
- Integridad de los datos: el análisis utilizó un conjunto de datos completo sin valores faltantes (NMissing = 0), lo que garantiza la solidez del análisis de tendencias.
- Longitud de los datos:El análisis se basa en un conjunto de datos de 30 períodos de tiempo, lo que proporciona una base sólida para la evaluación de tendencias.

