Felix Savart, cirujano y físico francés nacido en junio 1791, formuló la Ley de Biot-Savart

Desde el punto de vista histórico, el mes pasado fue importante para la teoría electromagnética. Se trata de la Ley de Biot Savart, la cual establece que: La densidad de flujo magnético infinitesimal asociado es proporcional al elemento de longitud de circuito, la corriente que recorre cada elemento e inversamente proporcional al cuadrado de la distancia de ese punto. La dirección del campo magnético está en la dirección de dl×r. Ver Ec. 1, donde μ₀ es la permeabilidad del vacío, I es la corriente que fluye a través del elemento de camino dl y r es la posición en dicho camino (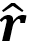 vector unitario).

$dB=\frac{{\mu }_0}{4\pi }\frac{Id\overrightarrow{l}x\hat{r}}{r^2}$                    Ec.1

La ley es válida en la aproximación magnetostática, y coherente tanto con la ley circuital de Ampère como con la ley de Gauss para el magnetismo [1]. Recibe su nombre de Jean-Baptiste Biot y Félix Savart, que descubrieron esta relación en 1820. Así, la ley de Biot-Savart puede utilizarse para calcular el campo magnético resultante de una distribución de corriente eléctrica.

Otras características notables sobre La ley de Biot-Savart son que es exactamente similar a la ley de Coulomb en electrostática y es relevante para conductores muy pequeños que transportan corriente. Para una distribución simétrica de corriente, dicha ley es aplicable. Ejemplo, la Ley de Biot Savart se puede utilizar para evaluar la respuesta magnética a nivel molecular o atómico. Por otra parte, se puede usar para evaluar la velocidad en la teoría aerodinámica inducida por la línea de vórtice. A continuación, hablamos sobre la Ley de Biot-Savart en el Electromagnetismo y su conexión con las Leyes de Maxwell. Adicionalmente ponemos énfasis en ejemplos realizados en COMSOL Multiphysics, donde se pone al campo magnético como protagonista.

Conexión con otras leyes en Electromagnetismo

Ley de Ampere

¿Cuál es la relación entre la Ley de Biot Savart y las Ecuaciones de Maxwell? [2], siendo las ecuaciones de Maxwell un conjunto de ecuaciones fundamentales que rigen el comportamiento de los campos eléctricos y magnéticos. En efecto, se puede derivar a partir de Maxwell, concretamente de la Ley de Ampere, que establece una conexión entre una corriente eléctrica y el campo magnético que genera.

Aunque la Ley de Biot Savart y la Ley de Ampere abordan los campos magnéticos, su enfoque y aplicabilidad difieren. Por ejemplo, la Ley de Biot Savart es más útil para calcular campos magnéticos debidos a bucles de corriente o conductores irregulares portadores de corriente. En cambio, la Ley de Ampere se adapta mejor a geometrías simétricas y corrientes estacionarias.

Ley de Faraday

La relación entre la Ley de Biot Savart y la Ley de Faraday es intrigante. Por un lado, la Ley de Biot Savart se refiere al campo magnético generado por una corriente. Por otro lado, la Ley de Faraday trata de la fuerza electromotriz (FEM) inducida en un conductor debido a un campo magnético cambiante. Juntas, estas leyes forman la base de la inducción electromagnética, que sustenta el funcionamiento de generadores eléctricos, transformadores e inductores.

La teoría electromagnética sólo estaría completa si se abordara el concepto de campo eléctrico. Al igual que los campos magnéticos, los campos eléctricos son conceptos fundamentales del, originados por las cargas eléctricas. La Ley de Coulomb rige la interacción entre cargas eléctricas, estableciendo paralelismos con la Ley de Biot Savart, que trata de los campos magnéticos generados por corrientes eléctricas.

Algunas aplicaciones

Las aplicaciones prácticas de la Ley de Biot Savart son abundantes, desde el diseño y análisis de electroimanes y generadores hasta la determinación del momento magnético de un bucle de corriente, parámetro esencial en magnetostática. La ley también ha contribuido significativamente al desarrollo de tecnologías como la resonancia magnética (RM), los aceleradores de partículas y los dispositivos de almacenamiento magnético.

La versatilidad de la Ley de Biot Savart queda patente en su capacidad para calcular campos magnéticos de distintas geometrías. Desde un hilo recto o un solenoide hasta configuraciones más complejas como bobinas toroidales o en forma de silla de montar, esta ley es una herramienta fiable para comprender el comportamiento de los campos magnéticos en distintos escenarios.

Electromagentismo en COMSOL Multiphysics

COMSOL Multiphysics posee diferentes módulos que se basan en su totalidad o bien están relacionados con fenómenos electromagnéticos. Tales módulos son AC/DC, RF, Wave Optics, Ray Optics, Plasma and Semiconductor [3]. No obstante, el módulo por excelencia y que permite estudiar muchos casos o situaciones distintas para dispositivos electromagnéticos es el módulo AC/DC. A continuación, revisamos algunos ejemplos para visualizar la utilidad del software en esta área.

Ejemplo 1

Este modelo se trata de una corriente variable en el tiempo que induce un campo magnético variable en el tiempo [4]. El campo magnético induce corrientes en los conductores vecinos. Las corrientes inducidas se denominan corrientes parásitas. En este modelo, el fenómeno se ilustra mediante una simulación de campo armónico en el tiempo, así como un análisis transitorio, en el que se estudian las corrientes de Foucault resultantes de la conexión de la fuente. Se tienen dos bobinas portadoras de corriente sobre una placa de cobre. Las bobinas están rodeadas de aire y hay un pequeño entrehierro entre ellas y la placa metálica. La fuente externa se aplica como densidad de corriente, pero la densidad de corriente total en las bobinas sólo se obtiene teniendo en cuenta las corrientes inducidas. El caso armónico en el tiempo muestra el efecto Skin. Esto quiere decir que la densidad de corriente es alta en la proximidad de la superficie y disminuye rápidamente en el interior del conductor.

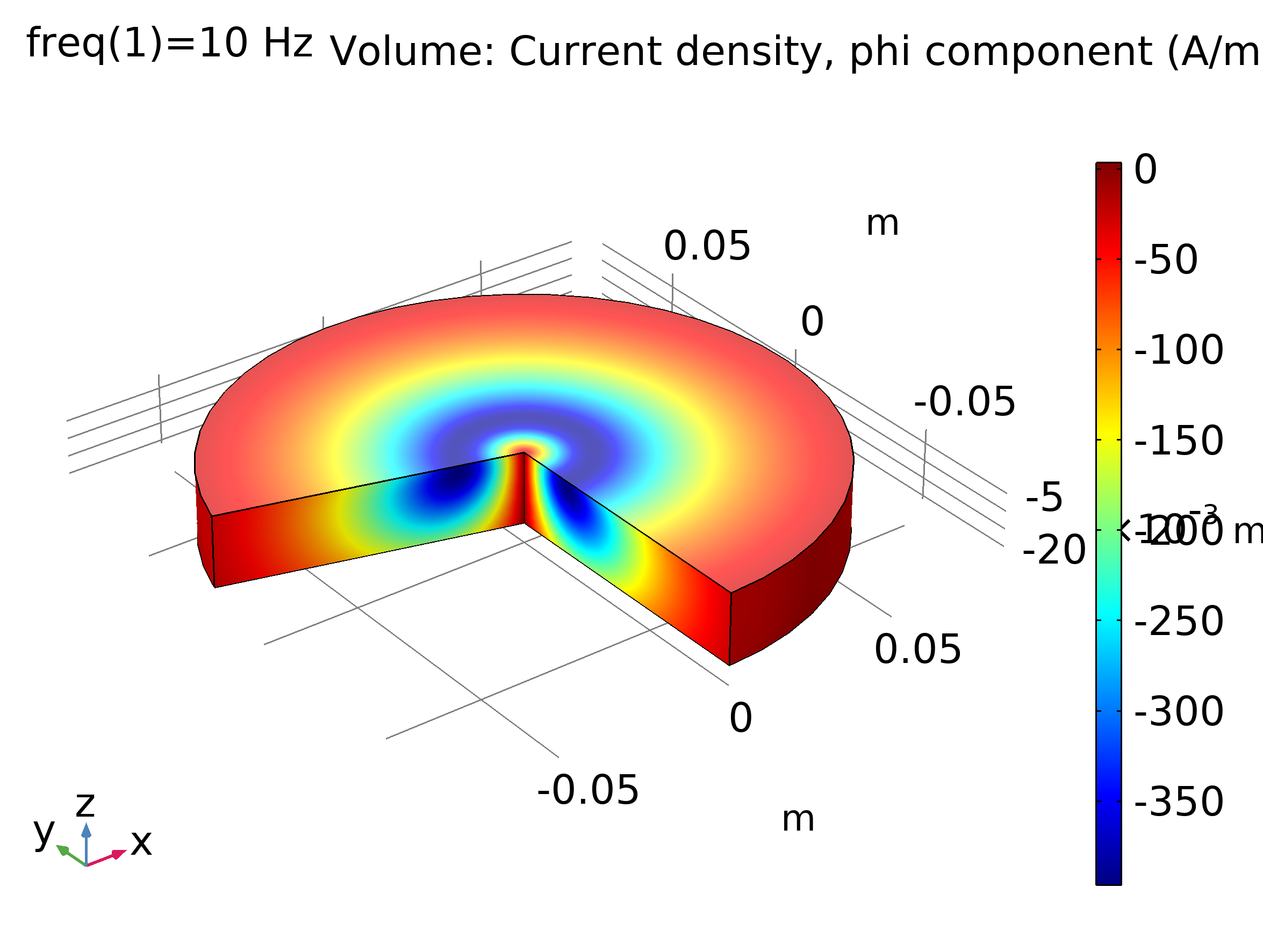
Fig. 1. Componente angular Phi de la densidad de corriente a una frecuencia de 10 Hz. Ver modelo en [4].

Ejemplo 2

El modelo se llama An Electrodynamic Levitation Device – el cual trata el acoplamiento dinámico electromagnético y la dinámica de cuerpos rígidos [5]. Una fuerza de levitación electrodinámica se produce por las corrientes inducidas cuando un disco conductor se coloca por encima de dos bobinas concéntricas que llevan corrientes variables en el tiempo en direcciones opuestas. Se resuelve la dinámica del disco levitante y se compara con los datos medidos en la bibliografía.

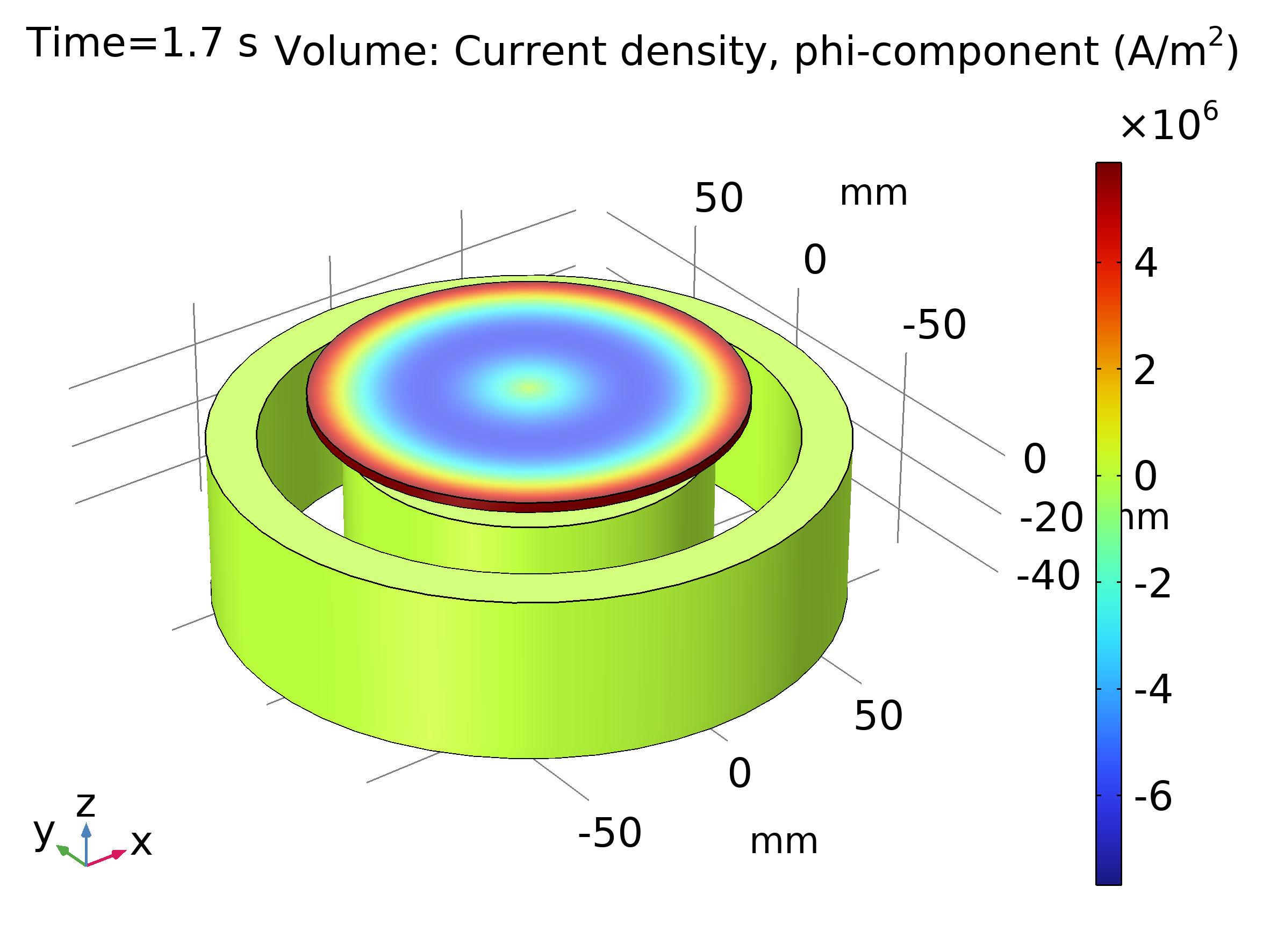
Fig. 2. Componente angular Phi de la densidad de corriente a los 1.7 s en el dispositivo. Ver modelo en [5].

Ejemplo 3

Otro modelo relevante para aprender es el de una máquina de transporte marítimo que se desplaza por la superficie o bajo el agua como un submarino, dando lugar a perturbaciones locales detectables en el campo magnético terrestre [6]. Dichas perturbaciones pueden utilizarse para activar sistemas de armamento. La firma magnética de un submarino puede reducirse generando un campo magnético que se contrapone de intensidad y dirección adecuadas basado en el conocimiento previo de las propiedades magnéticas del submarino.

Este modelo demuestra una poderosa técnica en este tipo de modelado al tratar la cubierta metálica como caras 2D incrustadas en una geometría 3D. Así, se requieren mallas de 2D comparativamente más sencillas que el caso 3D. A continuación, se resuelve una proyección tangencial de la ecuación 3D en la malla de caras 2D.

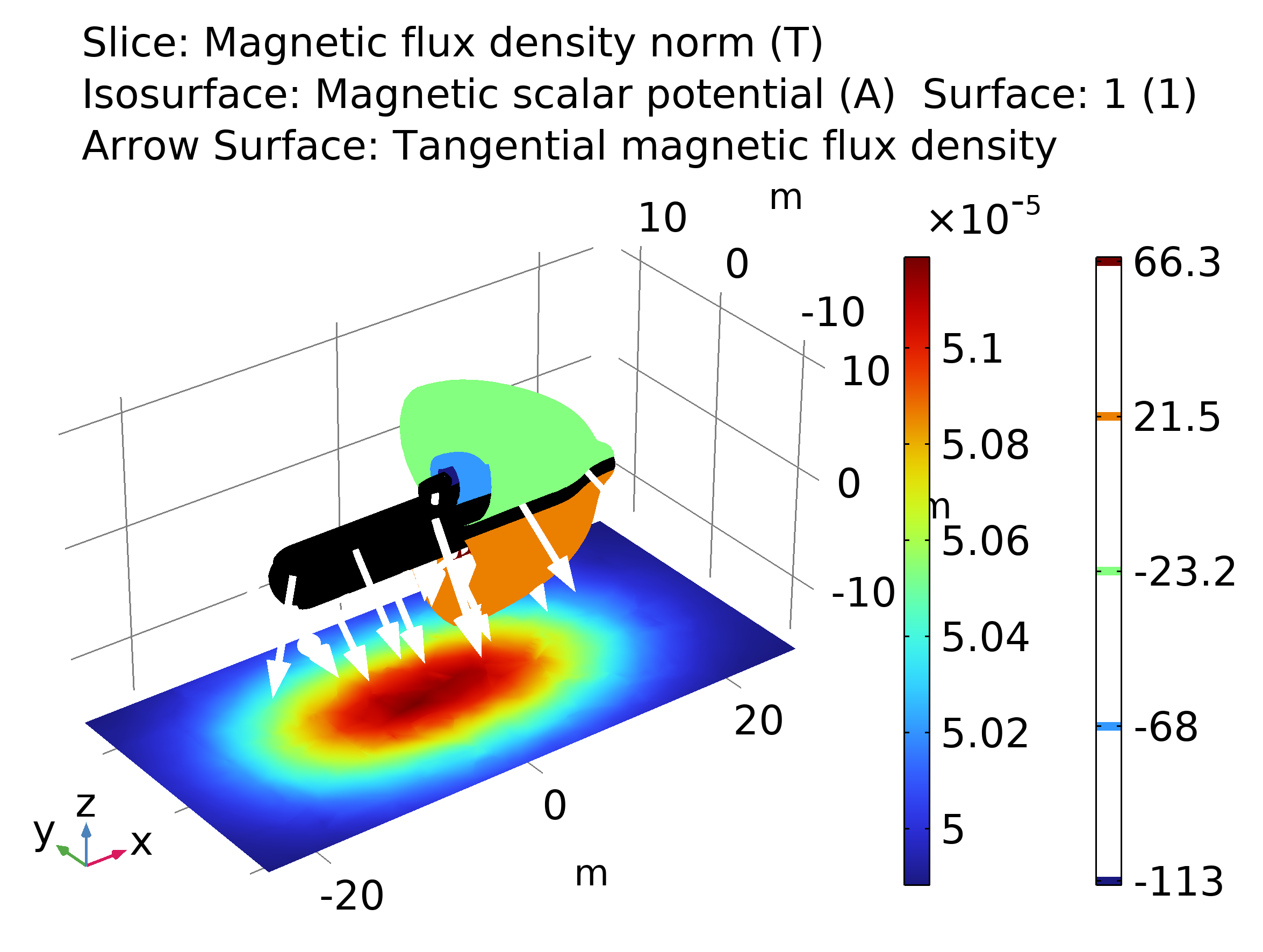
Fig. 3. Magnitud de la densidad de flujo magnética, potencial escalar magnético y componente tangencial de la densidad de flujo magnética para el submarino. Ver modelo en [6].

Referencias

[1] https://www.comsol.com/multiphysics/electromagnetics
[2] https://iopscience.iop.org/article/10.1088/0305-4470/20/8/022/pdf
[3] https://www.comsol.com/blogs/computational-electromagnetics-modeling-which-module-to-use/
[4] https://www.comsol.com/model/induction-currents-from-circular-coils-124
[5] https://www.comsol.com/model/an-electrodynamic-levitation-device-14221
[6] https://www.comsol.com/model/magnetic-signature-of-a-submarine-291