La Teoría de la Relatividad y más en COMSOL Multiphysics
- Detalles
- Categoría: Comsol
- Visto: 5753
El 11 de abril se cumplen 109 años del día en que Albert Einstein (1879-1955) reveló su Teoría de la Relatividad. Sus teorías llevaron a reinventar nuestra comprensión del mundo, convirtiéndose en un icono cultural y figura mundial. Einstein se convirtió en todo esto y más cuando sus teorías de la relatividad especial y general fueron reconocidas como grandes pilares de la física y de la cosmología. El ganador del Premio Nobel revolucionó las ideas aceptadas sobre el tiempo y el espacio para desarrollar sus teorías. Fue uno de los primeros en profundizar en el nuevo campo de la mecánica cuántica, trabajando sobre el efecto fotoeléctrico y la naturaleza de la luz.
La Relatividad y COMSOL Multiphysics
Lente gravitacional
COMSOL permite estudiar fenómenos donde la Teoría de la Relatividad entra en juego. Por ejemplo, el efecto de lente gravitacional [1] se modela usando un índice de refracción que varía continuamente en el espacio, lo cual se conoce como medio graduado. El índice de refracción, n, depende de la constante gravitacional G (unidad SI: m3/(kg·s2), la masa solar m0 (unidad SI: kg), la velocidad de luz c (unidad SI: m/s), y la distancia radial desde el centro del sol r (unidad SI: m), ver Ecuación 1, donde r=√(x2+y2+z2)

La constante gravitatoria es una constante física incorporada con el nombre G_const y con valor predefinido 6.67384×10-11[m3/(kg·s2)]. En este ejemplo, se liberan dos rayos, que rozan la superficie del sol y luego continúan hasta alcanzar una distancia de 150 millones de km. En este punto se evalúa el ángulo de desviación de los rayos desde su dirección inicial. Ver Figura 1.
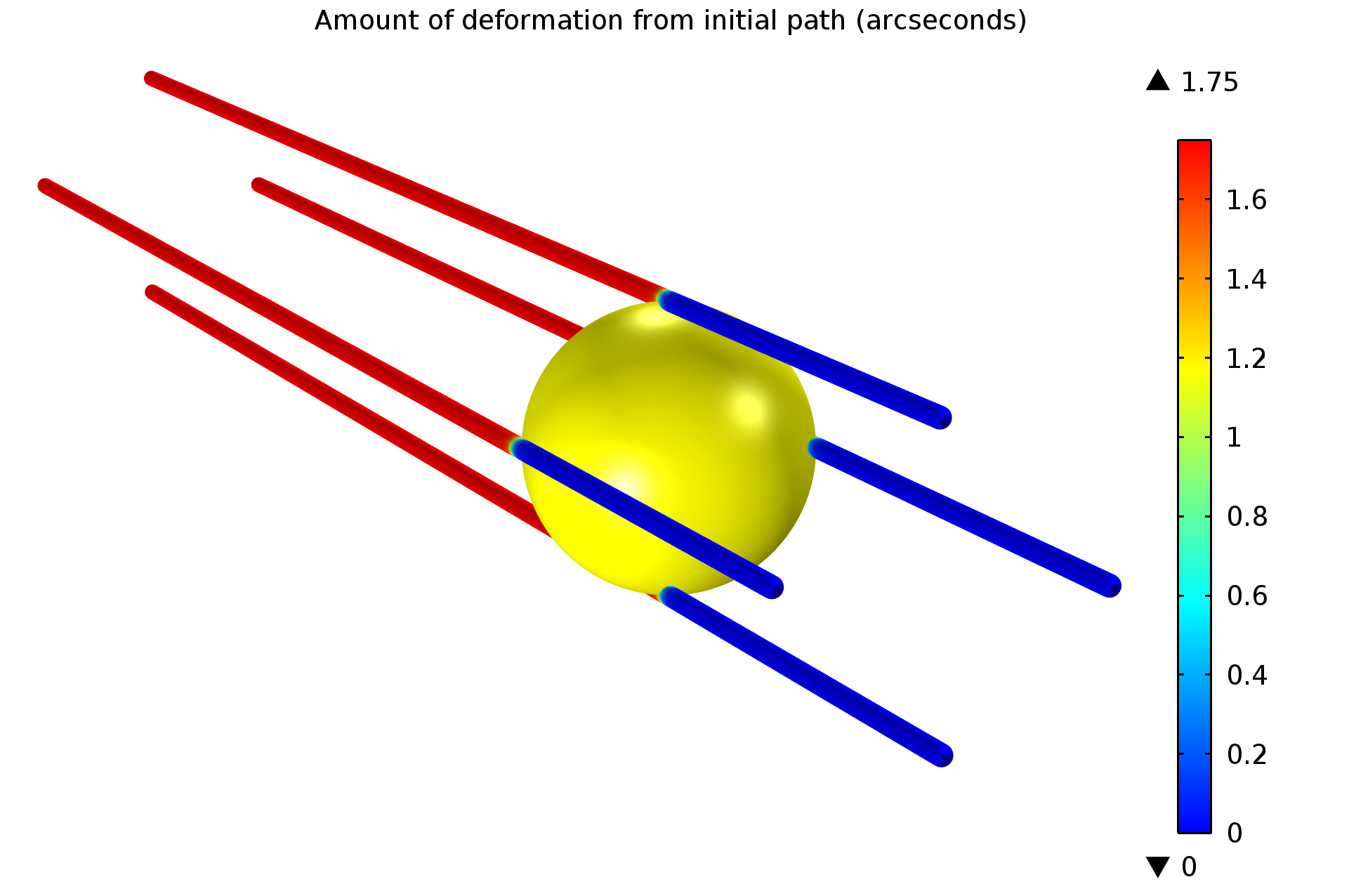
Figura 1: Deformación desde el camino óptico inicial.
El cambio angular en la dirección de los rayos se representa en la Figura 2. Después de la liberación, los rayos necesitan alrededor de 165s para llegar al sol. Los rayos entonces comienzan a desviarse de su dirección inicial debido al gradiente en el índice de refracción. El valor final es de aproximadamente 1,75 segundos de arco, consistente con la predicción de Einstein.
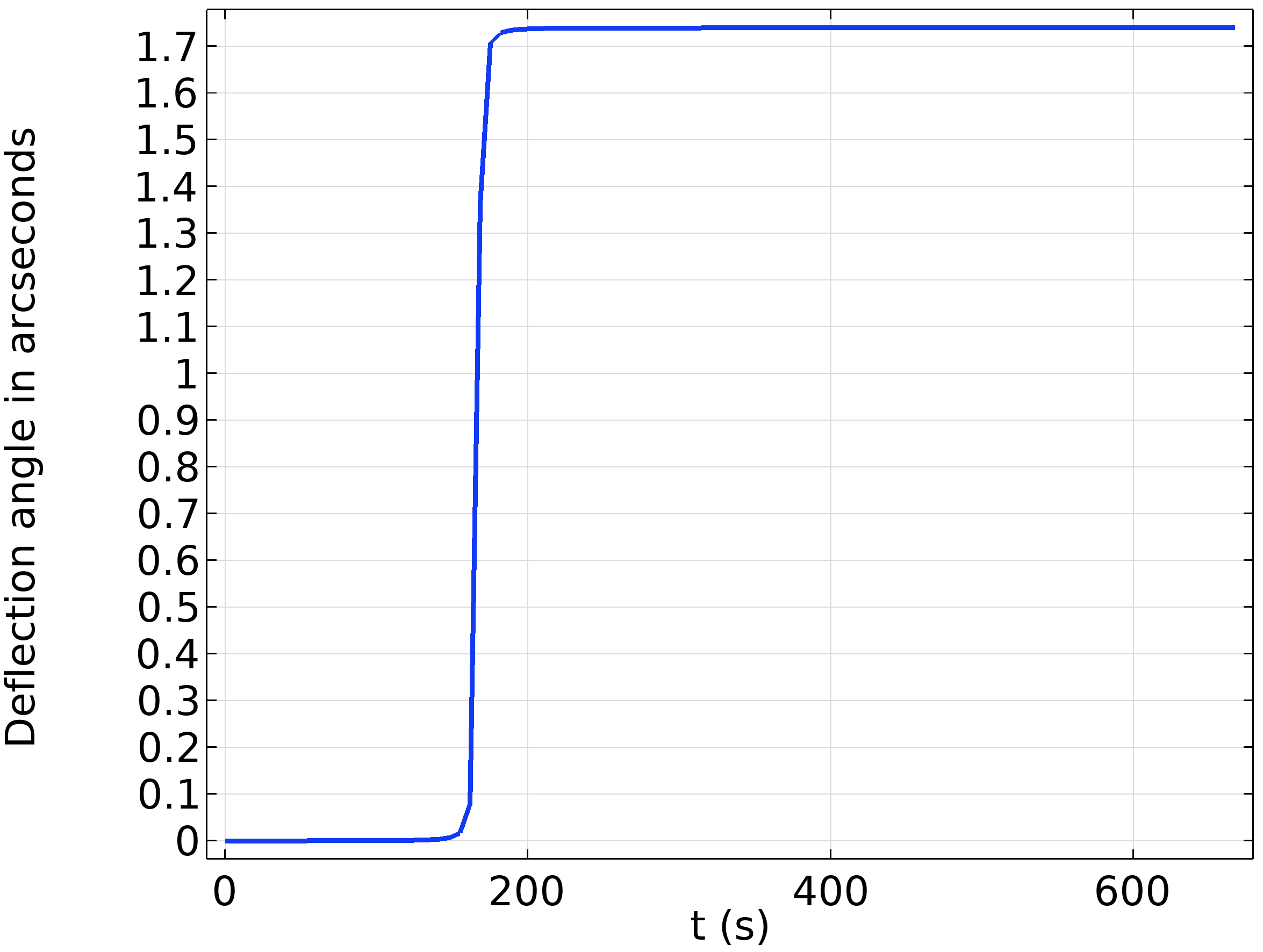
Figura 2: Ángulo de desviación causado por el campo gravitatorio del sol.
Protones en el campo magnético terrestre
Otro gran ejemplo es cuando existen partículas cargadas en las cercanías de la Tierra y son afectadas por el Campo Magnético [2]. En efecto, la Tierra tiene un campo magnético sustancial que se extiende hacia afuera por miles de kilómetros. El campo magnético es generado posiblemente por corrientes circulantes dentro un núcleo líquido de metal girando. Este campo magnético se parece mucho a un campo dipolar; habiendo una inclinación entre el eje de giro de la Tierra y el eje del dipolo magnético.
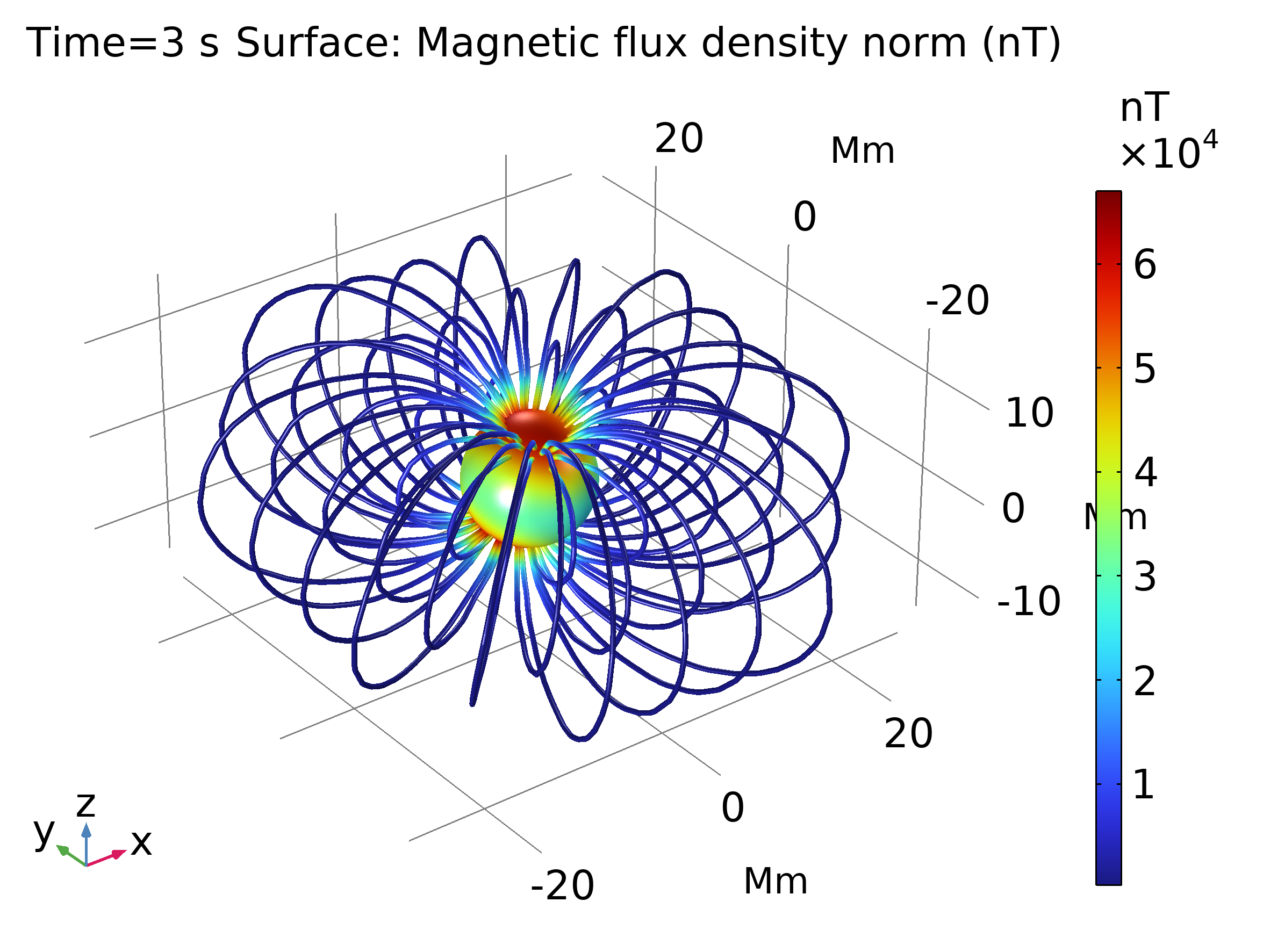
Para modelar la trayectoria de las partículas, se usa una formulación newtoniana (Ecuación 2), y se aplica una corrección relativista a la masa de los protones estudiados (Ecuación 3). La intensidad de la densidad de flujo magnético y la trayectoria de los protones se ve en la Figura 3 (mr se refiere a masa en reposo del protón).

 |
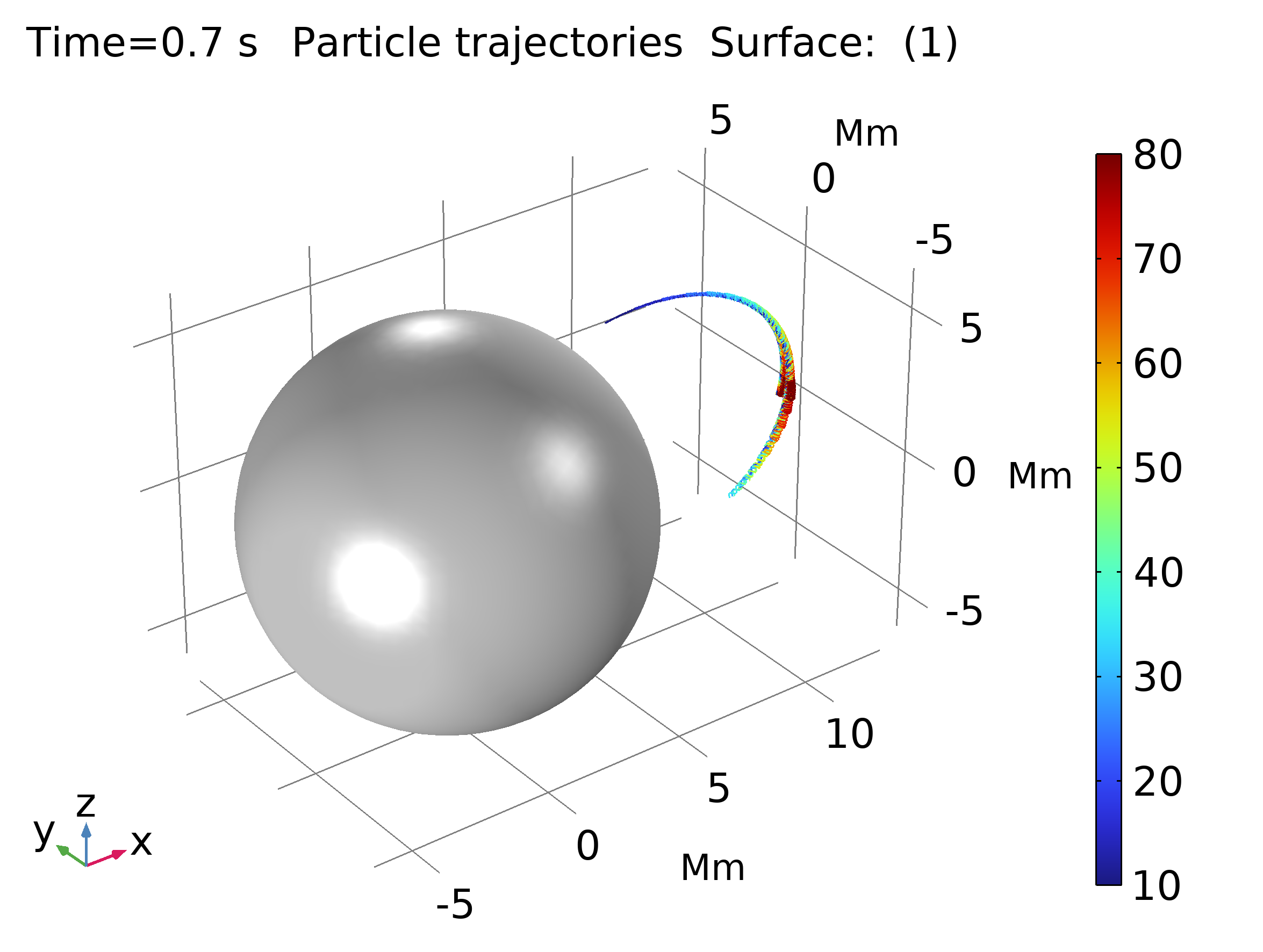 |
| Figura 3. Izquierda: Intensidad de la densidad de flujo magnética. Derecha: Trayectoria de las partículas. | |
Divergencia en un haz de electrones
Un ejemplo similar al anterior permite modelar la propagación de un haz de partículas cargadas a altas corrientes y con velocidades relativistas [3]. Así, la masa de la partícula es corregida mediante la ecuación 3, con la única diferencia que las partículas son ahora electrones. En este escenario, la carga espacial y la corriente del haz crean fuerzas eléctricas y magnéticas significativas que tienden a expandir y enfocar el haz, respectivamente. La interfaz de Charged Particle Tracing puede usar un procedimiento iterativo para calcular de manera eficiente las trayectorias de las partículas fuertemente acopladas y campos eléctricos y magnéticos para un haz operando a corriente constante. En este ejemplo se utilizan otras interfaces acopladas como Electrostatics y Magnetic Fields, ambas acopladas a Charge Particle Tracing. Las trayectorias de los electrones se visualizan en la Figura 4.
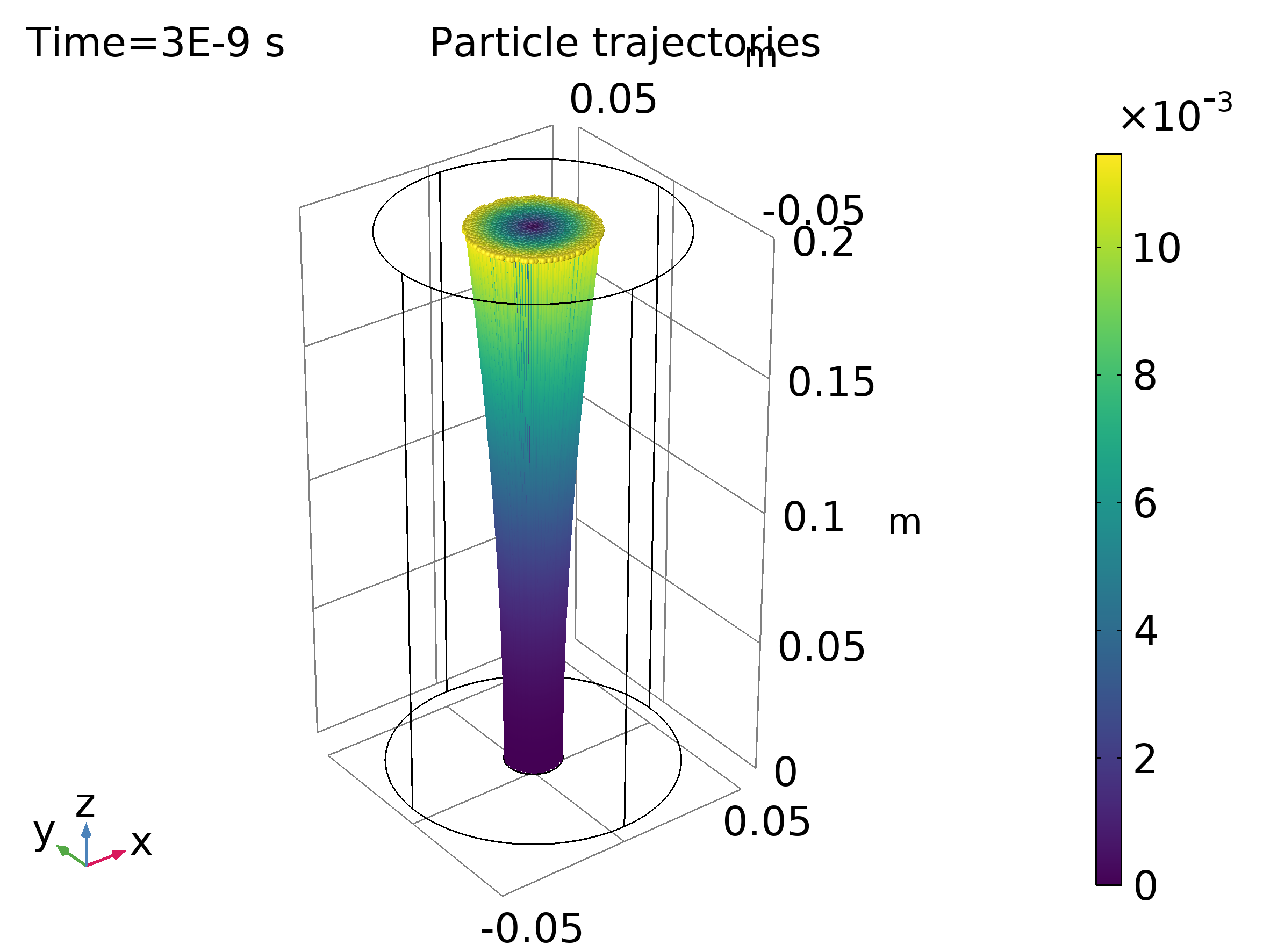
Figura 4: Trayectoria de los electrones.
Otros aportes y ejemplos
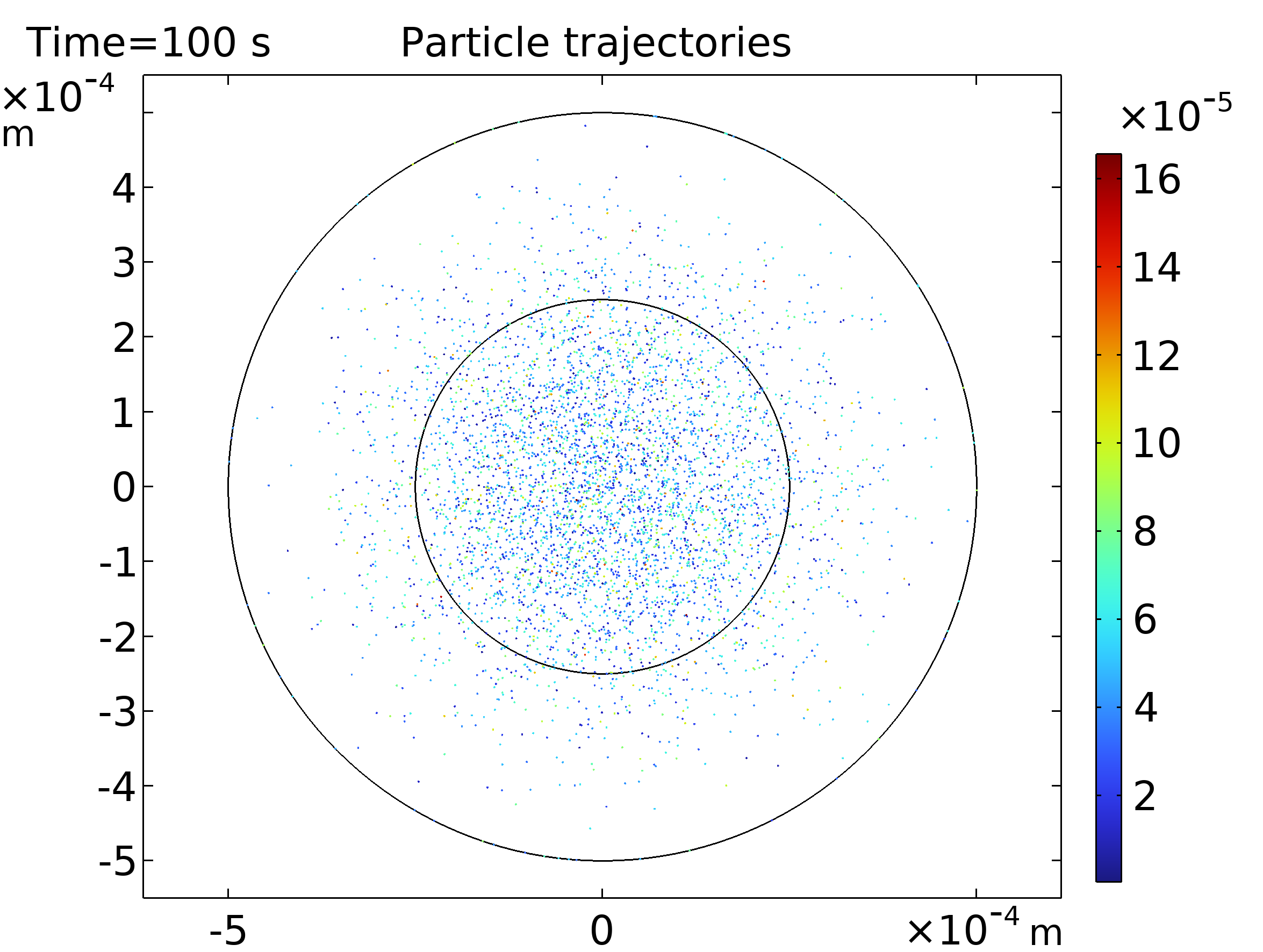
Einstein proporcionó la primera prueba científica de la existencia de los átomos con su teoría cuantitativa del movimiento browniano. Estudió colisiones atómicas en fluidos y demostró que se puede medir el tamaño de los átomos. Este fue un gran avance para el campo de la física atómica. El movimiento browniano sirve para modelar el transporte cuando es de naturaleza puramente difusiva. COMSOL permite hacer la comparación entre los resultados obtenidos utilizando Particle Tracing y Transport of Diluted Species. En la primera interfaz se añade un nodo para incluir la fuerza browniana. En la segunda interfaz se utiliza la ecuación de convección-difusión; sin embargo, deshabilitando la convección [4]. La comparación se puede ver en Figura 5.
 |
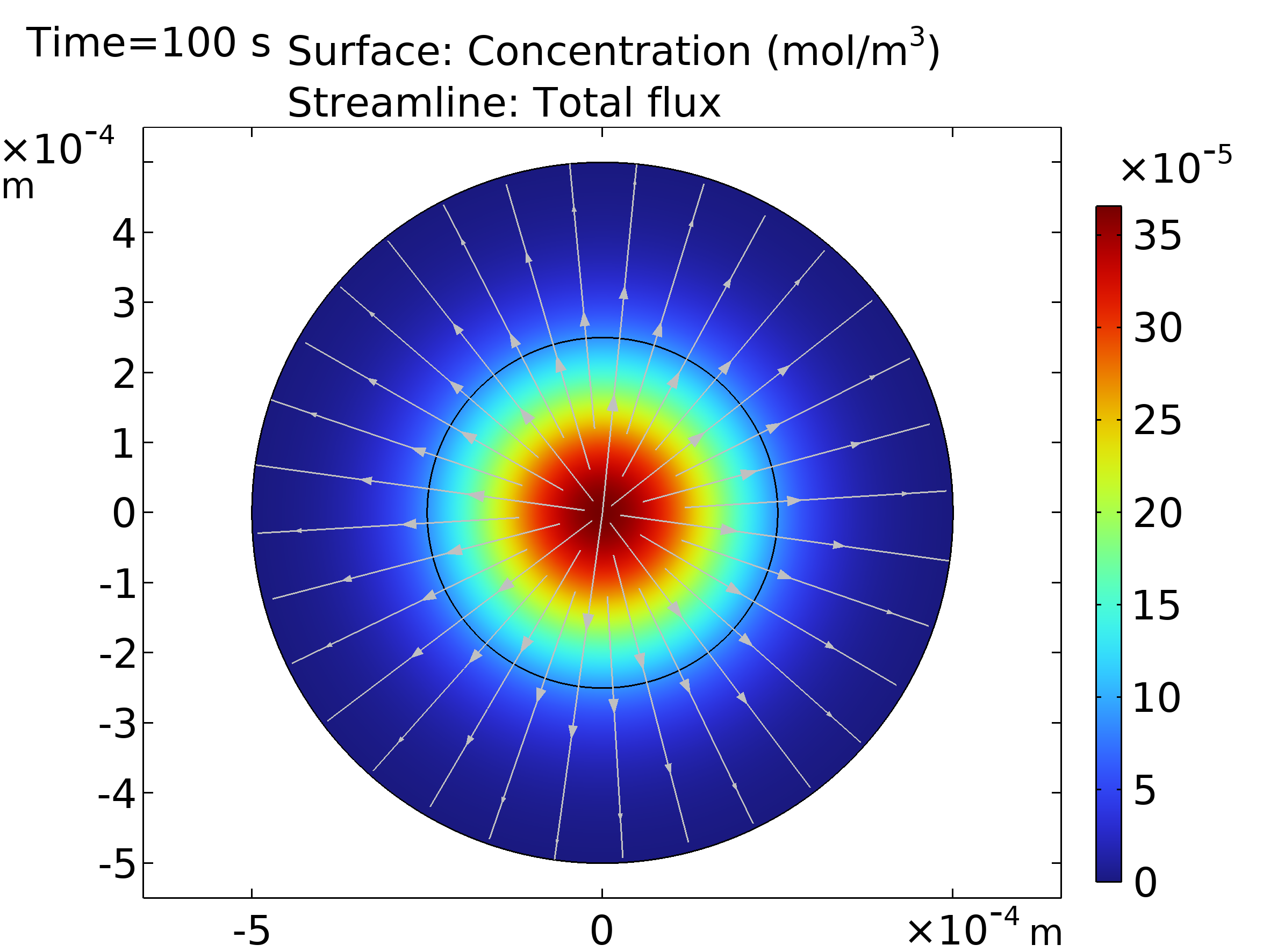 |
| Figura 5. Izquierda: Difusión de las partículas en un fluido usando Particle Tracing y demostrando el movimiento browniano. Derecha: Concentración después de 100 segundos usando of Diluted Species. | |
Referencias
[1] https://www.comsol.com/model/gravitational-lensing-18573
[2] https://www.comsol.com/model/motion-of-trapped-protons-in-earth-s-magnetic-field-19047
[3] https://www.comsol.com/model/relativistic-diverging-electron-beam-17065
[4] https://www.comsol.com/model/brownian-motion-12333

