Introducción

Muchas variables en biología no cumplen con los supuestos de los tests estadísticos paramétricos: no están distribuidas normalmente, las varianzas no son homogéneas, o ambas.

La utilización de un test estadístico paramétrico (como ANOVA o regresión lineal) sobre esos datos puede dar un resultado engañoso.

En algunos casos, la transformación de los datos hará que éstos se ajusten mejor a los supuestos. Existen infinitas transformaciones que se pueden utilizar, pero es mejor utilizar una transformación que se utilice habitualmente en su campo, como la tranformación de la raíz cuadrada para datos de conteo o la tranformación logarítmica para datos de tamaños, antes que una tranformación ambigua de la que no mucha gente haya oído hablar.

También es importante decidir que transformación utilizar antes de realizar el test estadístico.

Las transformaciones matemáticas sobre las variables se realizan a menudo para:

• incrementar la cercanía del ajuste (aumentar R-cuadrado) entre la ecuación de regresión y los puntos de datos,
  
  y/o para
  
  
• hacer que las variables se ajusten a los supuestos de los procedimientos estadísticos, como la normalidad, y obtener así toda la potencia de esos procedimientos.

Además, las transformaciones de ciertos tipos de variables a veces pueden hacer que las interpretaciones de los resultados de procedimientos estadísticos sean más fáciles y más profundas que sin las transformaciones.

El término "escalera de potencias" (ladder of powers) se refiere a una secuencia de transformaciones algebraicas que pueden realizarse sobre una variable para cambiar la forma de su distribución.

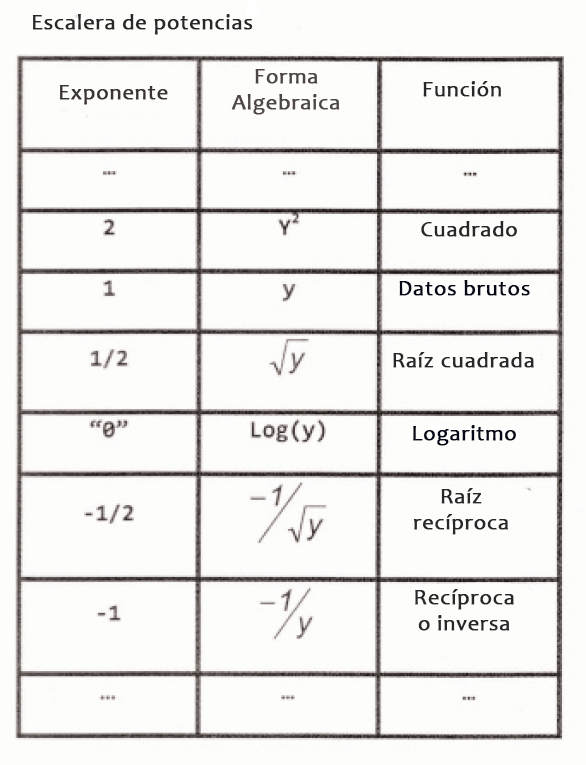
La escalera como se muestra en la tabla superior se enseña aquí para una variable etiquetada "y" que podría ser una variable dependiente o independiente.

Otras potencias y raíces se encajan entre las filas mostradas y se extienden tanto hacia arriba como abajo de la tabla.

Existen muchas transformaciones utilizadas en biología. Las más utilizadas son:

• Transformación raíz cuadrada. Consiste en hacer la raíz cuadrada de cada observación
• Transformación logarítmica. Consiste en tomar el logaritmo decimal de cada observación
• Transformación arcoseno de la raíz cuadrada. Consiste en tomar el arcoseno de la raíz cuadrada de un número.

Transformadas en SigmaPlot

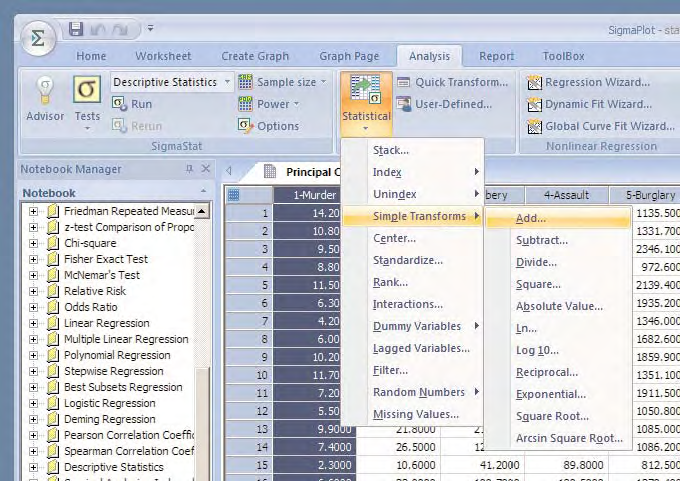
El camino de las transformadas en las nuevas versiones de SigmaPlot se muestra abajo:

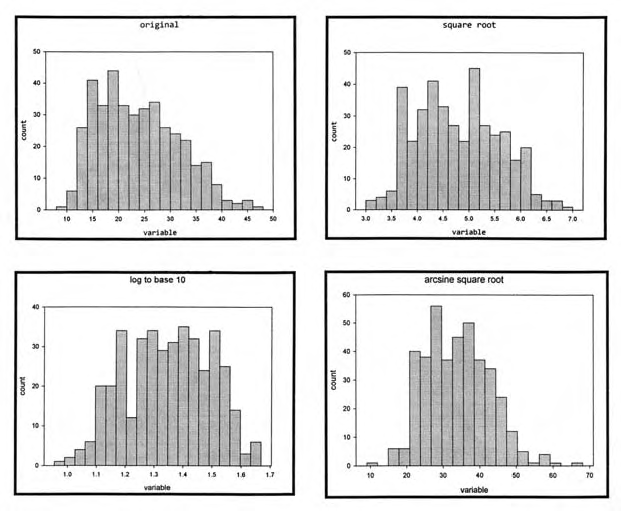
Algunos de los histogramas de las transformaciones de acuerdo con la escalera de potencias utilizando SigmaPlot se muestran en la cabecera del articulo junto con el histograma de los datos originales.