¿Utiliza la regresión lineal simple para la calibración de instrumentos? Descubra por qué la regresión ortogonal es un mejor enfoque
- Detalles
- Categoría: Minitab
- Visto: 7169
Los dispositivos de medición deben calibrarse regularmente para garantizar que realicen su trabajo correctamente. Si bien la calibración cubre una amplia gama de aplicaciones y escenarios, el objetivo es simple: asegurarse de que el dispositivo esté midiendo según sus estándares. La mayoría de los sistemas de calidad requieren un sistema de medición satisfactorio que incluya la calibración formal, periódica y documentada de todos los instrumentos de medición. Un problema común que enfrentan los ingenieros es cómo verificar que dos instrumentos miden partes de manera similar.
¿CÓMO DETERMINAR SI DOS INSTRUMENTOS PROPORCIONAN MEDICIONES COMPARABLES?
Un enfoque es comparar los dos instrumentos ajustando una línea de regresión lineal simple y luego usar el ajuste del modelo para ver si los valores son los mismos en todo el rango de mediciones. La regresión lineal simple modela la relación lineal entre dos variables continuas: una respuesta y un predictor.
EJEMPLO:
Supongamos que hay un fabricante de dispositivos médicos que quiere determinar si su monitor de presión arterial es equivalente a un modelo similar en el mercado. Para verificar que los dos instrumentos proporcionen mediciones comparables, el fabricante selecciona personas que representen un rango de valores donde las mediciones deben ser comparables. Luego se mide a las personas con ambos instrumentos. La empresa obtiene lecturas de presión arterial sistólica en una muestra aleatoria de 60 personas utilizando los dos instrumentos y registra los datos. Se muestra una muestra de las 60 filas, donde cada fila representa una medición usando los instrumentos Actual y Nuevo.
| Fila | Nuevo | Actual |
| 1 | 100 | 100 |
| 2 | 122 | 120 |
| 3 | 129 | 132 |
| 4 | 136 | 139 |
| 5 | 110 | 110 |
| 6 | 111 | 110 |
| 7 | 137 | 137 |
| 8 | 134 | 133 |
| 9 | 141 | 140 |
| 10 | 112 | 112 |
En este caso, se designan las lecturas actuales como la variable predictora (o X) y las lecturas nuevas como la variable de respuesta (o Y). Ajustar una línea de regresión a estos datos muestra que las lecturas del dispositivo de medición actual predicen bastante bien las lecturas del nuevo dispositivo de medición. El estadístico R-cuadrado indica que el dispositivo de medida Actual explica el 98,8% de la variación observada en el dispositivo de medida Nuevo.
La ecuación de regresión es:
Nuevo = 1.387 + 0.9894 Actual
.png)
A partir de estos datos, parece que las mediciones actuales ciertamente pueden predecir bastante bien las mediciones nuevas. En la práctica, vemos que los ingenieros utilizan modelos predictivos para confirmar que un nuevo dispositivo puede medir tan bien como un dispositivo actual. También hay otras aplicaciones; hay situaciones en las que se necesita una medición más rápida. Por ejemplo, algunas piezas o muestras deben medirse mediante mediciones de laboratorio antes de que puedan enviarse. Pero las mediciones de laboratorio pueden llevar horas según el proceso. Se puede utilizar un método de medición que proporciona resultados inmediatos para predecir las mediciones de laboratorio, proporcionando a los operadores e ingenieros información inmediata sobre posibles problemas.
El enfoque de regresión lineal simple es bueno cuando podemos suponer que no hay errores en la dirección horizontal o X. Para este ejemplo, esto implicaría que nuestro sistema de medición actual no contiene errores. En el caso de los sistemas de medición, sabemos que la suposición no es razonable, por lo que usar una regresión lineal simple no es el mejor enfoque estadístico. Pero no se preocupe, hay otro enfoque que es igual de fácil de usar.
¿QUÉ ES LA REGRESIÓN ORTOGONAL?
La regresión ortogonal, también conocida como regresión de Deming, se puede utilizar para determinar si dos instrumentos o métodos proporcionan mediciones comparables. La regresión ortogonal también examina la relación lineal entre dos variables continuas: una respuesta (Y) y un predictor (X). A diferencia de la regresión lineal simple (regresión de mínimos cuadrados), tanto la respuesta como el predictor en la regresión ortogonal contienen errores de medición. Recuerde que en la regresión simple, solo la variable de respuesta contiene error de medición. Si utiliza la regresión simple para determinar la comparabilidad cuando ambas variables contienen errores de medición, los resultados dependen de qué variable se supone que no tiene errores de medición en los cálculos. La regresión ortogonal aborda este problema, por lo que los roles de las variables tienen poca influencia en los resultados.
En la regresión lineal simple, el objetivo es minimizar la suma de las distancias verticales al cuadrado entre los valores y y los valores correspondientes en la línea ajustada. En la regresión ortogonal, el objetivo es minimizar las distancias ortogonales (perpendiculares) desde los puntos de datos hasta la línea ajustada. Si bien la diferencia entre estos enfoques puede parecer menor, al evaluar las medidas y las piezas en relación con las especificaciones, podría generar conclusiones significativamente diferentes.
Analicemos los datos del monitor de presión arterial usando la regresión ortogonal.
La regresión ortogonal requiere que se especifique la proporción de la varianza del error en X (Actual) e Y (Nuevo). Cuando el método de medición para X e Y es el mismo, es probable que las varianzas sean iguales, lo que daría como resultado una razón igual a 1. Pero es una buena práctica estimarla. Antes de la recopilación de datos para la regresión ortogonal, los ingenieros realizaron estudios separados en cada monitor para estimar la variación de la medición. La relación de varianza del error se calculó realizando un estudio independiente de repetibilidad y reproducibilidad del sistema de medición para cada dispositivo de medición para producir una componente de varianza para la Repetibilidad para cada dispositivo. La relación de las dos componentes de varianza para las estimaciones de repetibilidad se puede utilizar como entrada para el campo de relación de varianza del error. La varianza para el nuevo monitor fue 1.08. La varianza del monitor de la otra empresa fue de 1,2. El ingeniero decide asignar el monitor Nuevo para que sea la variable de respuesta y el monitor Actual de la otra empresa para que sea la variable de predicción. Con estas asignaciones, la relación de varianza del error es 1,08/1,2 = 0,9.
RESULTADOS DE LA REGRESIÓN ORTOGONAL
El gráfico de línea ajustada muestra que los puntos se encuentran cerca de la línea de regresión, lo que indica que el modelo se ajusta a los datos. Aquí mostramos el ajuste por mínimos cuadrados y el ajuste ortogonal. Las dos ecuaciones ajustadas se ven en la parte inferior izquierda de la imagen.
La Ecuación de Regresión Ortogonal es: Nuevo = 0.644 + 0.995 Actual
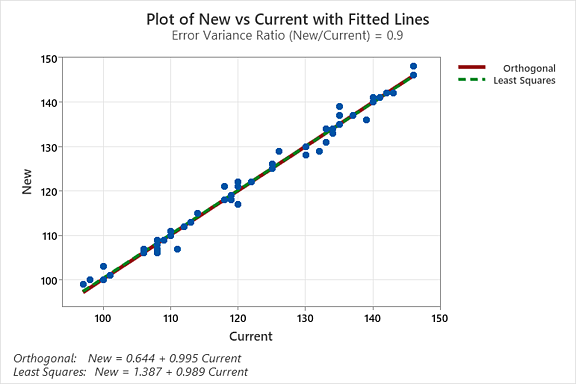
Tenga en cuenta que aunque las líneas parecen muy similares, la ecuación de regresión ortogonal es diferente de la ecuación de regresión lineal simple. Podemos usar la ecuación de regresión ortogonal para comprender la equivalencia de los dos instrumentos de medición.
Si alguna de las siguientes condiciones es verdadera, los resultados proporcionan evidencia de que los monitores de presión arterial no son equivalentes:
- El intervalo de confianza para la pendiente no contiene 1.
- El intervalo de confianza para la constante no contiene 0.
coeficientes
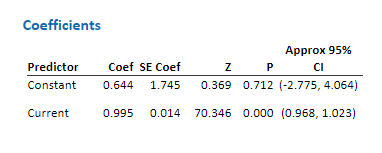
Por lo general, un nivel de confianza del 95% funciona bien. Un nivel de confianza del 95% indica que si se toman 100 muestras aleatorias de la población, los intervalos de confianza para aproximadamente 95 de las muestras contendrían el valor real del coeficiente. Para un conjunto de datos dado, un nivel de confianza más bajo produce un intervalo más estrecho y un nivel de confianza más alto produce un intervalo más amplio.
Los resultados muestran que el intervalo de confianza para la constante, que es de aproximadamente -2,78 a 4,06, contiene 0. El intervalo de confianza para la pendiente, Actual, que es de aproximadamente 0,97 a 1,02, contiene 1. Estos resultados no proporcionan evidencia de que las medidas de los monitores difieren. Con base en estos resultados, la compañía puede concluir que su nuevo dispositivo de medición funciona tan bien como el dispositivo actual en el mercado.
CONCLUSIÓN
Al calibrar dos sistemas de medición, la regresión ortogonal puede determinar si los instrumentos o métodos proporcionan mediciones comparables. A diferencia de la regresión lineal simple (también conocida como regresión de mínimos cuadrados), tanto la respuesta como el predictor en la regresión ortogonal contienen errores de medición. Usando la regresión ortogonal, el fabricante de dispositivos médicos puede concluir con confianza que su instrumento de medición es equivalente al instrumento de medición actual en el mercado actual.
La regresión ortogonal está disponible en la mayoría de los paquetes estadísticos, incluido Minitab Statistical Software.

