Ajuste de curvas con regresión lineal y no lineal con Minitab
- Detalles
- Categoría: Minitab
- Visto: 89314

A menudo pensamos en una relación entre dos variables como una línea recta. O sea, si se incremente un predictor en 1 unidad, la respuesta siempre crece en X unidades. Sin embargo, no todos los datos tienen una relación lineal, y el modelo debe de ajustarse a las curvas que presentan los datos.
¡Este gráfico de línea ajustada muestra la tontería de utilizar una línea para ajustar una relación curva!
¿Cómo ajustamos una curva a los datos? Afortunadamente, Minitab Statistical Software incluye una variedad e métodos de ajuste de curvas tanto en regresión lineal como no lineal.
Para comparar estos métodos, ajustaremos modelos a la algo complicada curva del gráfico de línea ajustada. Para otros propósitos, consideraremos que estos datos vienen de un proceso físico de bajo ruido que tiene una función curva. Queremos predecir con precisión la salida dada la entrada.
Ajustar curvas con términos polinomiales en regresión lineal
La forma más común de ajustar curvas a los datos utilizando la regresión lineal es incluir términos polinomiales, como predictores cuadráticos o cúbicos.
Típicamente, se escoge el orden del modelo por el número de curvas que se necesitan en la línea. Es muy raro utilizar más que un término cúbico.
El gráfico de los datos parece tener una curva, por lo que intentaremos ajustar un modelo lineal cuadrático utilizando Estadística > Regresión > Gráfica de línea ajustada
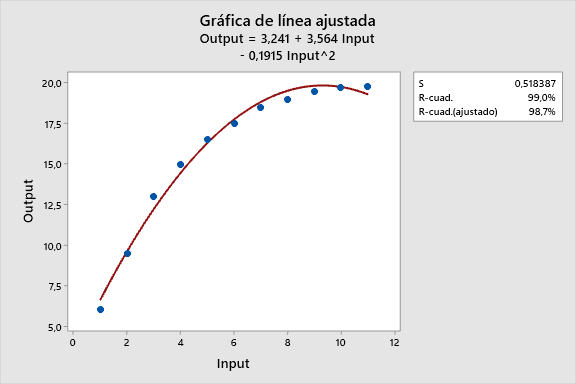
Mientras el coeficiente de determinación R-cuadrado (R2) es alto, el gráfico de línea ajustada muestra que la línea de regresión sistemáticamente sobre- e infra- predice los datos en diferentes puntos de la curva. Esto muestra que uno no siempre se puede fiar de un R-cuadrado alto.
Veamos si podemos hacerlo mejor.
Ajuste de curvas con términos recíprocos en regresión lineal
Si los datos de respuesta descienden a un suelo, o ascienden a un techo a medida que la entrada crece (por. ej., se aproximan a una asíntota), se puede ajustar este tipo de curva en una regresión lineal incluyendo el recíproco (1/X) de una variable predictora más en el modelo. De forma más general se desea utilizar esta forma cuando el tamaño del efecto para una variable predictora decrece cuando su valor crece.
Como la pendiente es una función de 1/X, la pendiente se hace más plana cuando crece X. Pare este tipo de modelo, X nunca puede ser igual a 0 porque no se puede dividir por cero.
Observando los datos, parece que se aplanana y se aproximan a una asíntota en algún punto alrededor de 20.
Utilizando Calc > Calculadora para crear una columna 1/Input (InvInput). ¡Veamos cómo funciona! Lo ajustamos tanto con un modelo lineal (arriba) como con uno cuadrático (abajo).
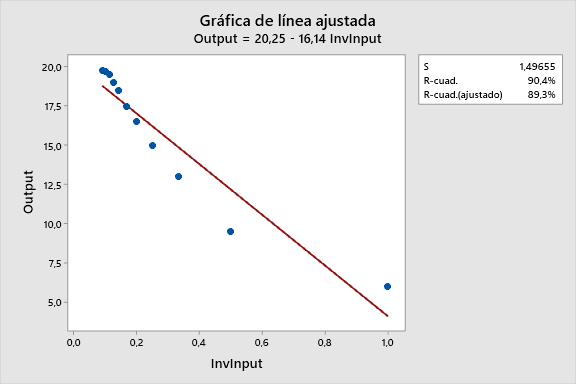
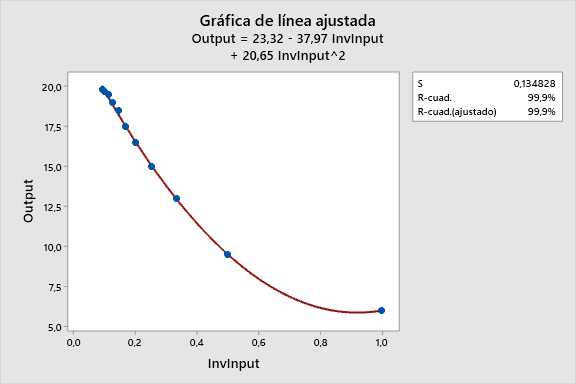
Para este ejemplo en particular, el modelo recíproco cuadrático se ajusta a los datos mucho mejor. El gráfico de línea ajustada cambia el eje X a 1/Input, por lo que es difícil de ver la curvatura natural de los datos.
En la gráfica de dispersión inferior, se utilizan las ecuaciones para dibujar los puntos ajustados para ambos modelos en la escala natural. Los puntos de datos verdes claramente se acercan más a la línea cuadrática
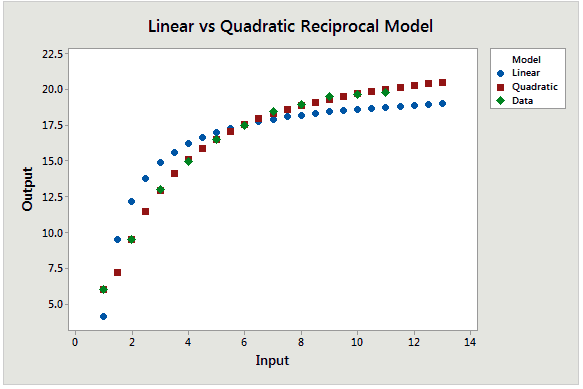
Comparado con el modelo cuadrático, el modelo recíproco con el término cuadrático tiene un valor S más bajo (bien), mayor R-cuadrado (bien), y no muestra predicciones desviadas. Así que hasta ahora este es nuestro mejor modelo.
Transformar las variables con funciones logarítmicas en regresión lineal
Una transformación logarítmica es un método relatívamente común que permite a la regresión lineal realizar ajustes de curvas que de otra forma solo serían posibles con regresión no lineal.
Por ejemplo, la función no lineal:
Y=eB0X1B1X2B2
puede expresarse en forma lineal como:
Ln Y = B0 + B1lnX1 + B2lnX2
Se puede tomar el logaritmo de ambos lados de la ecuación, como arriba, lo que se conoce como la forma doble logaritmo. O se puede tomar el logaritmo de solo un lado, conocida como la forma semilogaritmo. Si se toman los logaritmos en el lado del predictor, puede ser para todos o solo algunos de los predictores.
Las formas funcionales logarítmicas pueden ser bastante potentes, pero existen demasiadas combinaciones para entrar en detalles en esta visión general. La elección de doble logaritmo versus semilogaritmo (para la respuesta o los predictores) depende de la especificidad de los datos y del conocimiento del área temática. En otras palabras, si se coge este camino se necesitará investigar un poco.
Volviendo al ejemplo. Para datos donde la curva se aplana a medida que el predictor crece, un modelo semilogarítmico de los predictores puede ajustar. ¡Intentémoslo!
El gráfico de línea ajustada de Minitab dispone convenientemente de la opción para transformar logarítmicamente uno o ambos lados del modelo. Así que se ha transformado solo la variable predictora en el gráfico de línea ajustada inferior.
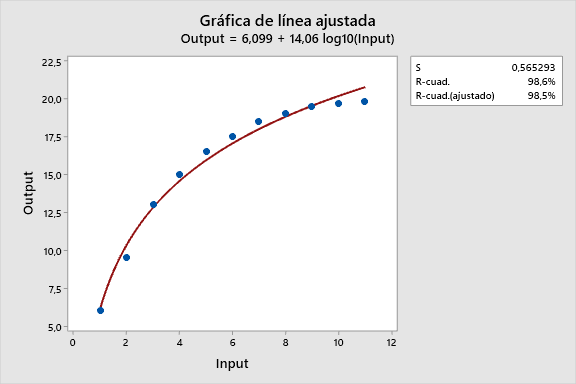
Visualmente podemos ver que el modelo semilogarítmico sistemáticamente sobre- e infra- predice los datos en diferentese puntos de la curva, igual que el modelo cuadrático. Los valores S y R-cuadrado también son virtualmente idénticos a los de ese modelo.
Hasta aquí, el modelo lineal con los términos recíprocos todavía proporcionan el mejor ajuste para los datos curvos.
Ajuste de curvas con regresión no lineal
La regresión no lineal puede ser una potente alternativa a la regresión lineal porque proporciona la funcionalidad de ajuste de curvas más flexible. El truco es encontrar la función no lineal que mejor se ajusta a la curva específica de los datos. Afortunadamente Minitab proporciona herramientas para facilitarlo.
En el cuadro de diálogo Regresión no lineal (Estadísticas > Regresión > Regresión no lineal), entrar Output para Respuesta. Después haga clic en Usar catálogo para escoger entre las funciones no lineales que Minitab proporciona.
Sabemos que nuestros datos se aproximan a una asíntota, así que podemos seleccionar en las dos funciones de Regresión Asintótica. La versión cóncava se ajusta más a nuestros datos. Seleccionamos esta función y hacemos clic en Aceptar.
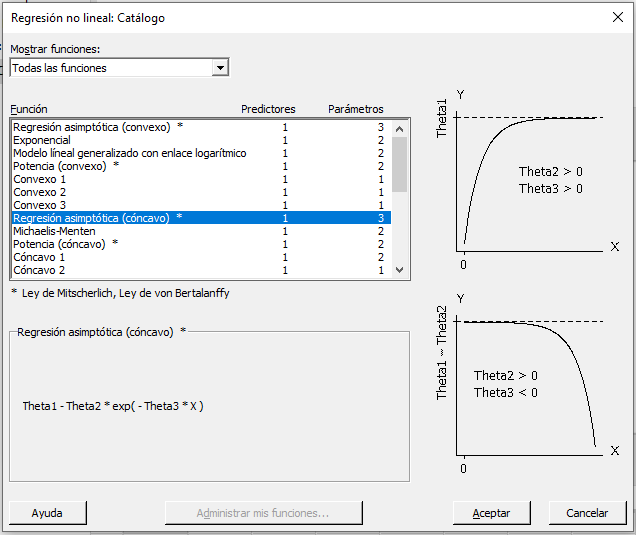
Después Minitab muestra un diálogo donde escogemos nuestro predictor.

Entre Input, clique Aceptar, y volvemos al diálogo principal.
Si hacemos clic en Aceptar del diálogo principal, Minitab muestra el siguiente cuadro de diálogo:

A diferencia de la regresión lineal, la regresión no lineal utiliza un algoritmo para encontrar el mejor ajuste paso a paso. Se necesita proporcionar los valores de arranque para cada parámetro de la función. ¡Vaya, no tengo ni idea! Por suerte Minitaba lo facilita.
Volvamos a la función que escogimos. ¡La figura lo facilita!
Nótese que Theta1 es la asíntota, o el techo, al que nuestros datos se aproximan. A la vista del primer gráfico de dispersión, eso ocurre aproximadamente en 20 para nuestros datos. Par un caso como el nuestro, donde la respuesta se aproxima a un techo cuando el predictor crece, Theta2 > 0 y Theta3 > 0.

Consecuentemente entramos lo siguiente en el cuadro de diálogo:
- Theta1: 20
- Theta2: 1
- Theta3: 1
Después de entrar esos valores, volvemos al diálogo principal, clicamos Aceptar, y ¡voila!


Es imposible calcular R-cuadrado para la regresión no lineal, pero el valor S para el modelo no lineal (0.179746) es prácticamente tan pequeño como el del modelo recíproco (0.134828). Queremos un valor S pequeño porque significa que los puntos de los datos caen más cerca de la línea curva de ajuste. El modelo no lineal tampoco tiene una desviación sistemática.
Comparación de la efectividad del ajuste de curvas de los diferentes modelos
| Modelo | R-cuadrado | S | Ajuste desviado |
| Recíproco-cuadrático | 99.9 | 0.134828 | No |
| No lineal | N/A | 0.179746 | No |
| Cuadrático | 99.0 | 0.518387 | Sí |
| Semilogarítmico | 98.6 | 0.565293 | Sí |
| Recíproco-lineal | 90.4 | 1.49655 | Sí |
| Lineal | 84.0 | 1.93253 | Sí |
Tanto el modelo lineal con el término recíproco cuadrático como el modelo no lineal vencen a los otros modelos. Estos dos modelos superiores producen predicciones igualmente buenas para la relación curva. Sin embargo, el modelo de regesión lineal con los términos recíprocos también produce valores-p para los predictores (todos significativos) y un R-cuadrado (99.9%), ninguno de los cuales puede obtenerse para un modelo de regresión no lineal.
Para este ejemplo, estas estadísticas extra pueden ser convenientes para un informe, aunque los resultados no lineales sean igual de válidos. Sin embargo, en casos donde el modelo no lineal proporciona el mejor ajuste, se debería de proceder con el mejor ajuste.
Últimos pensamientos
Si se tiene una curva difícil de ajustar, encontrar el modelo correcto puede parecer una tarea inmensa. Sin embargo, después de todo el esfuerzo para obtener los datos, vale la pena encontrar el mejor ajuste posible.
Al especificar cualquier modelo, debería permitir que la teoría y el conocimiento sobre el área temática le guíe. Algunas áreas tienen prácticas y funciones estándar para modelar los datos.
Si bien se desea un buen ajuste, no se desea inflar artificialmente el R-cuadrado con un modelo demasiado complicado. Hay que ser consciente que:
- R-cuadrado puede ser engañoso
- Los modelos demasiado complicados pueden producir resultados engañosos
- Verificar los gráficos residuales evita resultados engañosos (no se han mostrado en este artículo, pero el autor los revisó).

