Por Jim Frost

En análisis de regresión, se desea que el modelo de regresión tenga variables significativas y obtener un valor R² alto. Esta combinación bajo P valor/alto R² indica que cambios en los predictores están relacionados con cambios en la variable de respuesta y que el modelo explica mucha de la variabilidad de la respuesta.

Esta combinación parece ir junta de forma natural. Pero ¿qué pasa si tu modelo de regresión tiene variables significativas pero explica poco la variabilidad? Tiene bajos valores P y bajos coeficientes de determinación R².

A primera vista, esta combinación no tiene sentido. ¿Son los predictores de significancia todavía significativos? ¡Veamos esto!

Comparación de modelos de regresión con bajos y altos valores R²

Es difícil comprender esta situación utilizando únicamente números. La investigación muestra que los gráficos son esenciales para interpretar correctamente análisis de regresión. ¡La comprensión es más fácil cuando se puede ver lo que está pasando!

Con esto en mente, utilizaremos gráficos de líneas ajustadas. Sin embargo, un gráfico 2D de líneas ajustadas puede visualizar únicamente los resultados de una regresión simple, que tiene una variable predictiva y la respuesta. Los conceptos son ciertos para la regresión lineal múltiple, pero no se puede graficar las mayores dimensiones que se requieren.

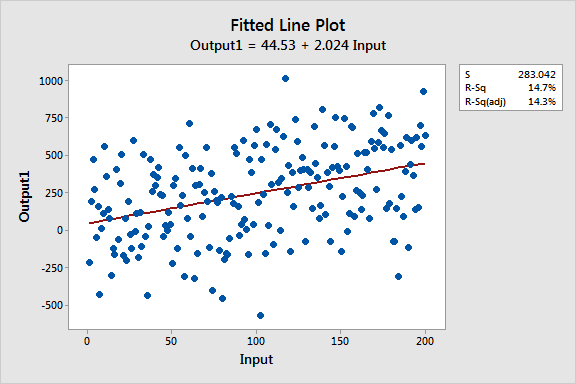
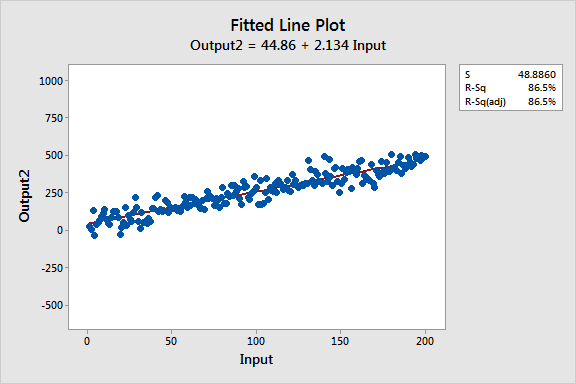
Estos gráficos de líneas ajustadas muestran dos modelos de regresión que tienen ecuaciones de regresión prácticamente idénticas, pero el modelo superior tiene un bajo valor R² mientras que el otro lo tiene alto. Se han mantenido las escalas de los gráficos constantes para una comparación más fácil. Aquí están los datos para estos ejemplos.

Similaridades entre los modelos de regresión

Los dos modelos son prácticamente idénticos en varios ámbitos:

• Ecuaciones de regresión: Salida = 44 + 2 * Entrada
• Entrada es significativa con P< 0.001 para ambos modelos

Se puede ver que la pendiente creciente de las dos líneas de regresión es aproximadamente 2, y siguen con precisión la tendencia que está presente en ambos conjuntos de datos.

La interpretación del valor P y el coeficiente para la Entrada no cambia. Si se mueve a la derecha en cualquier línea incrementando Entrada en una unidad, existe un incremento medio de dos unidades en Salida. Para ambos modelos, el valor P significativo indica que se puede rechazar la hipótesis nula que el coeficiente es igual a cero (sin efecto).

Más aún, si se entra el mismo valor para Entrada en ambas ecuaciones, calculará valores de predicción prácticamente equivalentes para Salida. Por ejemplo, una entrada de 10 produce una salida pronosticada de 66.2 para un modelo y 64.8 para el otro modelo.

Diferencias entre modelos de regresión

Seguro que la principal diferencia es lo que primero se ve de estos gráficos de líneas ajustadas: La variabilidad de los datos alrededor de dos líneas de regresión es drásticamente diferente. R² y S (error estándar de la regresión) describen numéricamente esta variabilidad.

El gráfico de bajo R² muestra que, aunque ruidosos, los datos de alta variabilidad pueden tener una tendencia significativa. La tendencia indica que la variable predictiva todavía proporciona información sobre la respuesta aunque los puntos de los datos caigan lejos de la línea de regresión. Mantengamos este gráfico en mente para cuando intentemos reconciliar variables significativas con un bajo valor R²!

Como vemos, las dos ecuaciones de regresión producen predicciones prácticamente idénticas. Sin embargo, los niveles de variabilidad diferentes afectan a la precisión de estas predicciones.

Para calcular la precisión, miraremos los intervalos de predicción. Un intervalo de predicción es un rango que es probable que contenga el valor de respuesta de una nueva observación única dados unos ajustes especificados de los predictores en el modelo. Los intervalos más estrechos indican predicciones más precisas. Debajo se encuentran los valores ajustados y los intervalos de predicción para una Entrada de 10.

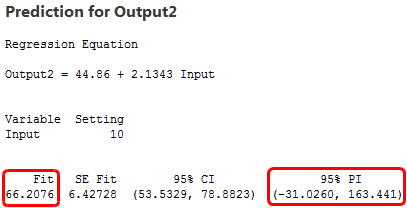
El modelo con los datos de alta variabilidad produce un intervalo de predicción que se extiende entre aproximadamente -500 a 630, ¡más de 1100 unidades! Mientras tanto, el modelo de baja variabilidad tiene un intervalo de predicción entre -30 y 160, aproximadamente 200 unidades. Claramente, las predicciones son mucho más precisas para el modelo de alto R², aunque los valores ajustados sean prácticamente los mismos.

La diferencia en precisión debería tener sentido después de ver la variabilidad presente en los datos reales. Cuando los puntos de los datos se dispersan más, las predicciones deben de reflejar que añaden incerteza.

Reflexiones finales

Recapitulando lo que hemos aprendido:

• Los coeficientes estiman las tendencias mientras que R² representa la dispersión alrededor de la línea de regresión.
• Las interpretaciones de las variables significativas son las mismas tanto para modelos con alto y bajo R².
• Los valores R² bajos son problemáticos cuando se necesitan predicciones precisas.

¿Entonces, qué hacer si se tienen predictores significativos pero una bajo valor R²? Alguno dirá, “añadir más variables al modelo!”

En algunos casos, es posible que los predictores adicionales puedan incrementar la potencia explicativa verdadera del modelo. Sin embargo, en otros casos, los datos contienen un cantidad inherentemente más alta de inexplicable variabilidad. Por ejemplo, muchos estudios psicológicos tienen valores R² menores que 50% porque la gente es impredecible.

Las buenas noticias son que incluso cuando R² sea bajo, los valores P bajos indican una relación real entre los predictores significativos y la variable respuesta.