¿Qué sucede cuando el software matemático es realmente fácil de usar?

Dr. Roberto López, profesor emérito de matemáticas en el Intituto de Tecnología Rose-Hulman y Maple Fellow

Resumen:

Este artículo examina el aumento, el declive y el resurgimiento del uso de los sistemas de álgebra computacional (CAS) en el aula de matemáticas. Desde la emoción que rodea al potencial de la tecnología para revolucionar la enseñanza de las matemáticas, se exploran las dificultades que impidieron que esta visión se realizara por completo, y luego introduce un avance fundamental en el mundo de CAS que finalmente pone el sueño de la educación matemática moderna y efectiva a nuestro alcance.

La ambición de hacer que un sistema de álgebra computacional sea la "herramienta de primer recurso para enseñar, aprender y hacer" matemáticas se expresó en la subvención de 1987 de la National Science Foundation (NSF) que financió el primer paso para llevar ordenadores al aula en el Rose-Hulman Institute of Technology (RHIT). Las primeras clases CAS se impartieron en el otoño de 1988, y en 1991 se impartieron los cinco cursos de matemáticas requeridos para estudiantes de ingeniería y ciencias. En 1995, el Instituto adoptó una política de ordenadores portátiles, y el sueño de un servidor matemático ubicuo estaba a las puertas.

El movimiento de reforma del cálculo de mediados a finales de la década de los 80 indujo a muchos pioneros a establecer laboratorios de computación que ejecutaban alguna forma de CAS y a probar diferentes paradigmas para incorporar esta tecnología en el currículo. Al mismo tiempo, varios investigadores en educación matemática estudiaron y enunciaron un paradigma para el uso de esta tecnología. Capturado en la frase "habilidades y conceptos de resecuenciación", este paradigma sugería que se utilizara el CAS para presentar los conceptos "primero" antes que hacer énfasis en las capacidades de manipulación concomitantes. Una vez que el concepto había sido digerido, las habilidades necesarias se podían explorar en el CAS y luego dominarlas en la medida necesaria para un entorno manual.

Video: Los profesores están utilizando Maple en sus aulas para proporcionar una experiencia de aprendizaje atractiva y efectiva para sus estudiantes

¡Gloriosa visión! Los profesores realmente enseñan matemáticas, dando énfasis en la comprensión conceptual del material, involucrando a los estudiantes con ideas, no con ejercicios. Los estudiantes realmente aprenden y absorben ideas matemáticas, sin tener que esforzarse en manipulaciones para las que no encontraría ningún propósito. ¿Pero qué fue mal? ¿Por qué se desvaneció esa visión? A mediados de la década de los 1990, casi todas las herramientas CAS disponibles estaban dirigidas por comandos, excepto en Derive, que se abandonó en 2007. Esto requería que los estudiantes primeron aprendieran la herramienta antes de poder experimentar cualquiera de sus beneficios. Inicialmente, los pioneros que incluyeron en primera instancia el CAS a sus clases estaban dispuestos a "pagar el precio" de convencer a los estudiantes de que valía la pena aprender el lenguaje de un CAS. Pero este enfoque no se apoderó de quienes fueron llamados a dar soporte a la visión de los pioneros. Esto llevó a un desencanto gradual del potencial del CAS como herramienta de trabajo para la puesta en marcha de la formación matemática.

Otro obstáculo obstacle para una adopción mayoritaria de CAS como herramienta de trabajo fue la restricción que imponía el entorno de laboratorio en el proceso. Si los estudiantes incorporan el CAS como una actividad de laboratorio, éste no se integra en el plan de estudios y no puede convertirse en una herramienta de primer recurso. Los ejercicios de laboratorio obligatorios se consideran un trabajo adicional, más allá de las actividades manuales estándar endémicas de los cursos tradicionales. Los estudiantes son lo suficientemente inteligentes como para ver esto y se rebelan contra una tecnología que parece aumentar su carga de trabajo en lugar de disminuirla. Lo que está a prueba es lo que preocupa típicamente a los estudiantes, y si el test se hace con lápiz y papel, entonces esas son las capacidades que el estudiante quiere aprender.

Se necesitan tres cosas para que una nueva tecnología se afiance: aplicabilidad, accesibilidad y facilidad de uso. La nueva tecnología debe ser una mejora sobre los modos existentes. Desbe estar fácilmente disponible. Y tiene que ser fácil de implementar.

Seguramente un dispositivo informático que puede manipular símbolos y realizar casi todas las manipulaciones de los primeros años de matemática universitaria debería considerarse una herramienta útil. Que es útil para hacer matemáticas se evidencia por su uso en la industria y el comercio actuales. El hecho de que sea útil para enseñar y aprender matemáticas se evidencia por su aparición en numerosos cursos universitarios de matemáticas, ciencias e ingeniería.

El ordenador portátil (e incluso la avanzada calculadora "gráfica") prometió accesibilidad; la facilidad de uso era otro asunto. En la RHIT a principios de los 90, donde Maple había sido adoptado como el CAS estándar, una guía de sintaxis de 14 páginas era una ayuda necesaria al comienzo de la secuencia del cálculo, que a su vez tenía que ser modificada para permitir que los estudiantes adquirieran suficiente dominio de Maple para el meterial del curso real que se presentara en ese contexto. Las primeras tres semanas del primer trimestre se dedicaron a los temas de revisión que se incluyen en el curso. Temas como la resolución de ecuaciones, gráficos, encontrar funciones inversas, etc., se utilizaron como los campos de entrenamiento para dominar Maple. (Justo al principio se descubrió que intentar enseñar la sintaxis y los nuevos conceptos al mismo tiempo, simplemente, no funcionaba.) Hacia el final del segundo trimestre todos los temas tradicionales se habían tratado, la eficiencia de disponer de un CAS esencialmente compensaba el gasto del comienzo del primer trimestre aprendiendo Maple. (Esto cambió con el tiempo a medida que las nuevas versiones de Maple se hacían cada vez más fáciles de usar.)

Por qué Maple es mejor que una calculadora gráfica

Nótese, sin embargo, que no todo el esfuerzo de aprendizaje del uso de un CAS como herramienta de trabajo se centra en dominar la sintaxis de sus comandos. Lo que se observó en RHIT fue la lucha del estudiante con la estructura impuesta por la rigidez de un lenguaje de ordenador. Por ejemplo, los estudiantes querían "resolver" derivadas, integrales, límites, más que evaluarlos. Pues bien, el CAS tiene comandos específicos para estas acciones, y el mal uso de un comando por pereza lingüística lleva al estudiante a quedarse corto. En un entorno donde el curso basado en CAS podía evitarse, muchos estudiantes hicieron precisamente eso. En un entorno donde el CAS se ve como una carga adicional, no se afianza ni prospera.

Pero algunas tecnologías ya arraigaron en el pasado. Las matemáticas en la escuela secundaria en la década de 1950 incluían aprender a usar los logaritmos como herramientas para multiplicar y dividir números engorrosos. A principios de los 60 era imposible por los cursos de química y física (con sus laboratorios correspondientes) sin saber cómo usar una regla de cálculo. A principio de los 70 empezó a aparecer la calculadora de mano como herramienta de trabajo. De hecho, a mediados de los 70 las calculaoras que podían, con la entrada de un conjunto de datos de puntos, calcular todas las sumas y sumas de cuadrados y sumas de productos necesarios para realizar un ajuste de mínimos cuadrados de los datos, revolucionaron el laboratorio de estadística. Y cualquiera que todavía pueda calcular una raíz cuadrada a mano es una excepción, incluso en una reunión de matemáticos.

Los estudiantes no deberían tener que seguir cada uno de los pasos que sus instructores tuvieron que dar para obtener su nivel de competencia. En otras palabras no es necesario académicamente que la ontogenia recapitule la filogenia, una teoría biológica que sostiene que al desarrollarse desde el embrión hasta el adulto, los animales pasan por etapas que se asemejan o representan etapas sucesivas de sus remotos ancestros. Esta es una teoría evolutiva ampliamente desacreditada, pero parece sobrevivir en el currículo de matemáticas, que espera que los estudiantes lo absorban. No es necesario que todos los estudiantes que necesiten alguna comprensión matemática sean sometidos a un arduo curso de capacitación que conduzca a un grado avanzado en la materia. La única manera de romper los lazos que el currículo tradicional de matemáticas impuso a los estudiantes es adoptar el poder computacional de un CAS como la principal herramienta de trabajo. De hecho, como mínimo una empresa está asumiendo el papel líder en la promoción de nuevos currículos "basados en ordenadores" en todos los niveles de la educación matemática.

Un software potente y de fácil acceso puede ser la base para el nuevo aprendizaje en cursos CTIM (ciencias, technologia, ingeniería y matemáticas). Un ejemplo de por qué este autor descubrió ésto, surgió debido a su experiencia inicial con Maple en el aula en RHIT. Las series de Fourier (sumas de sinusoides que aproximan una función) fueron parte del currículo requerido. Los coeficientes de las sumas son los valores de ciertas integrales definidas. Antes de la disponibilidad de Maple, se observó que los estudiantes escribían un símbolo de suma, ejecutaban algunas integrales (normalmente mal) y utilizaban lo que era un conjunto de símbolos sin sentido. En clases después de la introducción de Maple, en las que los estudiante podían graficar la función y sus aproximaciones de Fourier propuestas, su comportamiento cambió. Ellos vendrían con gráficos que mostraran que sus aproximacioines no representaban a la función, pero ahora percibiendo que habían cometido un error. Su pregunta ahora era: basándonos en los gráficos, ¿podríamos ayudarlos a determinar qué error habían cometido? Obviamente, se había conseguido una comprensión conceptual significativa de una serie de Fourier.

Figura 1: Aplicación de la definición de la derivada a un polinomio

En la Figura 1, la definición de la derivada como el valor límite del cociente de la diferencia se aplica a un polinomio. Observese la pedagógica "resecuenciación" mediante la cual Maple primero proporciona el resultado final, y entonces se utiliza para implementar los pasos algebraicos de la derivación. Según la Figura 1, el polinomio se ingresa como la función y la definición de la derivada, es decir, el límite del cociente de la diferencia, se implementa a través de la notación matemática natural de Maple, tal como aparecería en un libro de texto. La evaluación es inmediata a través del menú contextual (un menú emergente desde el que se pueden seleccionar opciones), o de manera equivalente, a través del teclado. La derivada también se obtiene utilizando las notaciones de Newton y Leibniz, solo para verificar que estas notaciones significan exactamente lo que la definición afirma. Finalmente, los pasos algebraicos del cálculo se implementan en Maple, principalmente a través del sistema del menú contextual.

Otro ejemplo de las experiencias de este autor tiene que ver con la enseñanza de la integral definida como el límite de una suma de Riemann apropiada. Ahora, una suma de Riemann es la suma de productos de valores de la función y pequeños incrementos, la suma que representa el área aproximada bajo la gráfica de la función. Antes del advenimiento de la calculadora de mano, los intentos de enseñar este concepto haciendo aritmética a mano, escribiendo columnas de números en la pizarra, etc., eran totalmente inútiles. Este enfoque no atrajo la atención de los estudiantes más que unos pocos minutos, y el concepto nunca despegó. Con el advenimiento de la calculadora de mano, parecía que los estudiantes podían pasar por toda la aritmética para llegar a una aproximación significativa. Desgraciadamente, es imposible obligar a treinta estudiantes a presionar de manera uniforme y precisa todas las teclas correctas de una calculadora, incluso si todos los estudiantes tienen la misma calculadora. Y sin registro de qué teclas presionaron, incluso estos experimentos fueron un fracaso abismal.

Sin embargo, las herramientas de Maple hacen esta tarea transparente. Para comenzar, considérese la imagen del tutor de Riemann Sum en la Figura 2. La gráfica mostrada enseña cómo el área debajo de la gráfica de una función se aproxima por la suma de áreas de rectángulos equiespaciados debajo de la curva, y muy rápidamente permite al usuario ver el efecto de diferentes particiones y diferentes estrategias para formar la suma.

En la Figura 2, el tutor de sumas de Riemann se ha aplicado a la función en el intervalo. La partición predeterminada es de diez subintervalos iguales, y la suma predeterminada es una suma de los puntos medios. Las áreas reales y aproximadas debajo de la curva se dan debajo de la gráfica. A medida que se realizan diferentes elecciones de parámetros, el gráfico y los valores mostrados debajo se actualizan. Una interfaz como esta permite a los estudiantes explorar el concepto de la suma de Riemann sin la carga de tener que hacer o implementar los cálculos, y mucho menos dibujar las cifras correspondientes.

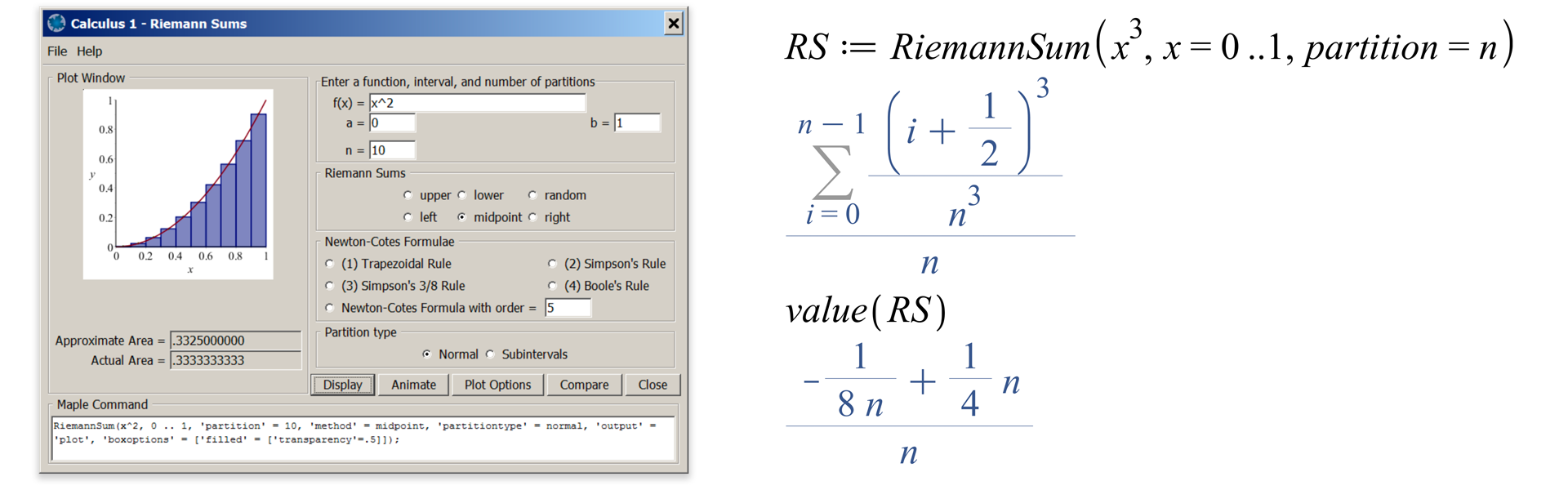
Figura 2 (izquierda): El tutorial de sumas de Riemann aplicado para f(x)=x² | Figura 3 (derecha): El comando RiemannSum con un indeterminado número de subdivisiones

El gráfico de la Figura 2 es dibujado por el comando RiemannSum que aparece al final del tutor en la Figura 2. Este comando también devolverá la suma de Riemann real, incluso una con un número indeterminado de subintervalos. En la Figura 3 se muestra un ejemplo de esto, donde, además, se ha aplicado el comando value para obtener una forma cerrada de la suma, una forma a partir de la que el límite puede ser determinado a medida que se hace infinito. Esto abarca la definición de la integral definida, y permite al estudiante ver la definición "en acción".

La Figura 4 de nuevo ilustra la definición de la integral definida, esta vez implementada con la tecnología libre de sintaxis "apuntar y clicar" de Maple. El integrando se define como una función a través del Menú Contextual emergente. Los operadores de límite y suma están implementados como plantillas de paleta. La evaluación del límite a la izquierda del sumatorio de riemann se realiza por el Menú Contextual. La matemática de la Figura 3 es exáctamente la matemática que un libro de texto utilizaría para expresar el mismo concepto. La observación más significativa es que Maple puede utilizar la misma notación, y que esta notación está conectada con el motor de cálculo subyacente.

Figura 4 (arriba): Implementación de Maple libre de sintaxis de la integral definida | Figura 5 (abajo): La suma de Riemann y su límite

Por supuesto, la suma de Riemann en si misma, y su forma cerrada equivalente, puede ser obtenida con su notación natural y sin la carga de una sintaxis especializada. En la Figura 5 se ven los pasos adicionales implementados mediante el Menú Contextual simplemente lanzando el sistema de menú emergente sobre las propias expresiones.

La suma de Riemann de la Figura 5 se construye a partir de una plantilla de paleta, y se evalúa con una expresión de forma cerrada invocando el Menú Contextual o su tecla equivalente. Esta transición requiere algunas habilidades algebraicas. En una clase tradicional, se debería de emplear un considerable tiempo y energía para este paso. Para cuando los estudiantes llegan a tener la suficiente capacidad para evaluar la suma de Riemann a mano, la conexión del proceso con la definición de la integral definida ya se ha evaporado. La adquisición de habilidades de manipulación manual interfiere con la absorción de los conceptos de alto nivel para los que la manipulación se supone que sirven. Si la herramienta con la que estas hacer estas manipulaciones fuera ella misma igual de difícil de dominar, sería un lavado - un proceso complicado reemplazado por otro. Que una herramienta como Maple pueda reemplazar fácil y naturalmente una manipulación tediosa es importante para la continuidad en la exposición de un concepto.

Se podrían dar innumerables ejemplos para respaldar el contenido de que las herramientas tecnológicas de un CAS no solo deben ser robustas y fácilmente disponibles , sino que también deben ser fáciles de aplicar. Pueden encontrarse ejemplos de cómo las herramientas en Maple satisfacen los requisitos de robustez y facilidad de uso en la sección Teaching Concepts with Maple de la web de Maplesoft. En esta página se pueden encontrar demostraciones grabadas en las que se resuelven problemas estándar de cálculo, ecuaciones diferenciales y álgebra lineal, con un paradigma "apuntar y clicar". De hecho, se listan más de 150 de estos ejemplos, no triviales, y se articulan utilizando herramientas integradas que requieren el uso de un único comando.

Se han adoptado nuevas tecnologías que mejoran las herramientas existenes. Incluso ha ocurrido en matemáticas cuando las reglas de tablas de logaritmos dieron paso a las calculadoras y después a los ordenadores. Pero el paso realmente radical de hacer que un CAS sea la herramienta de primer recurso para enseñar, aprender y hacer matemáticas todavía no ha ocurrido, en gran parte debido a que la curva de aprendizaje es demasiado pronunciada.

Excepto en Maple, donde la curva de aprendizaje es relativamente plana debido a su paradigma de facilidad de uso.

Como se muestra en los ejemplos de las Figuras 1-5 y en la página Teaching Concepts del sitio de Maplesoft, puede realizarse una importante exploración y resolución de problemasa matemáticos en Maple sin tener que hacer una inversión importante para aprender a utilizar la herramienta.

Esta simplicidad permite desarrollar la estrategia de resecuenciación de conceptos y habilidades. Gracias a que Maple es fácil de usar, la exploración de un nuevo concepto no lleva mucho tiempo. Las ideas matemáticas inherentes a un tema se pueden investigar, experimentar, manipular y aprender utilizando Maple como herramienta de trabajo, sin tener primero que dominar un conjunto de habilidades manipuladoras. Cuando el estudiante comprende por primera vez el concepto y ve cómo se relacionan los detalles con esa "imagen grande", el dominio de las habilidades manuales relevantes se lleva a cabo de forma mucho más efectiva y eficiente.