Las ecuaciones en derivadas parciales (EDP) son herramientas matemáticas fundamentales en la modelización de fenómenos físicos. Una de las EDP más importantes es la ecuación de Helmholtz, que surge en diversos contextos de la física y la ingeniería, incluyendo la acústica, el electromagnetismo y la mecánica cuántica. En este artículo, exploraremos la ecuación de Helmholtz y su aplicación en el estudio del experimento de doble rendija, un experimento clásico que demuestra la naturaleza ondulatoria de la luz y de otras partículas.

La ecuación de Helmholtz

La ecuación de Helmholtz se expresa generalmente como:

donde ∇² es el operador laplaciano, ψ es la función de onda y k es el número de onda, relacionado con la frecuencia de la onda y la velocidad de propagación. Esta ecuación describe cómo las ondas se propagan en un medio y se puede derivar de la ecuación de onda general en el caso de ondas estacionarias.

Aplicación en el experimento de doble rendija

El experimento de doble rendija, realizado por primera vez por Thomas Young en 1801, ilustra la interferencia de ondas. Cuando una onda de luz coherente (o cualquier otro tipo de onda) incide sobre dos rendijas estrechas, las ondas emergentes de cada rendija interfieren entre sí, creando un patrón característico de franjas brillantes y oscuras en una pantalla situada detrás de las rendijas. Ver referencia [1] para observar los patrones de difracción con el Double Slit Experiment.

Para modelar este fenómeno utilizando la ecuación de Helmholtz, consideramos la luz como una onda electromagnética. La ecuación de Helmholtz en dos dimensiones puede simplificarse para describir la propagación de la luz en el plano perpendicular a las rendijas. Si las rendijas están ubicadas en y=0 y están separadas por una distancia d, la solución de la ecuación de Helmholtz permite calcular la intensidad de la luz en cualquier punto de la pantalla.

La solución de la ecuación de Helmholtz en este contexto involucra considerar las condiciones de contorno y utilizar el principio de superposición de ondas. Las ondas emergentes de las dos rendijas se pueden representar como:

donde x y x′ son las posiciones relativas desde cada rendija hasta un punto en la pantalla. La interferencia de estas dos ondas produce un patrón de intensidad I dado por:

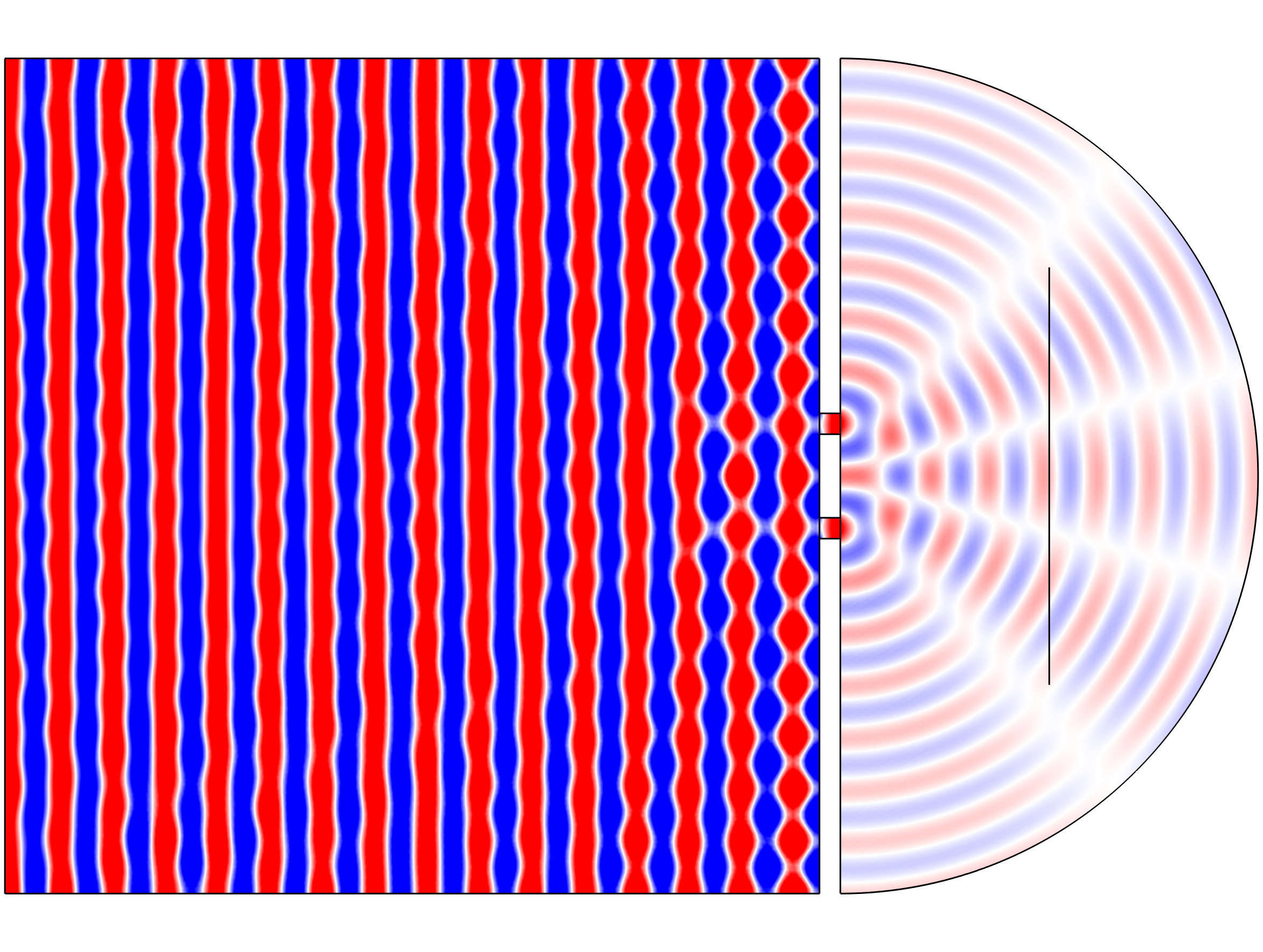
Al resolver esto, se obtiene el patrón de interferencia característico con máximos y mínimos en la intensidad de la luz, correspondiendo a las franjas brillantes y oscuras observadas en el experimento. Por ejemplo, ver modelo en la referencia [2]. A continuación, se ilustran algunos de los resultados, asumiendo un caso donde existen ondas de presión acústica. Una onda plana ingresa al dominio computacional desde la izquierda. Una parte de las ondas serán reflejadas y otra pasara a través de las rendijas hacia la derecha generando un patrón de interferencia. En la Figura de la cabecera se ilustra el patrón de interferencia del modelo [2] detrás de las rendijas. La amplitud decae hacia la derecha del Sistema. La amplitud por delante de las rendijas se incrementa debido a la reflexión.

Implicación

El uso de la ecuación de Helmholtz para modelar el experimento de doble rendija destaca cómo las EDP son esenciales para comprender y predecir fenómenos físicos. Este enfoque matemático no solo confirma la naturaleza ondulatoria de la luz, sino que también se extiende a otras áreas de la física, proporcionando un marco sólido para el estudio de la interferencia y la difracción de ondas. Así, el modelado con EDP, y en particular con la ecuación de Helmholtz, es una potente herramienta en la exploración de la naturaleza fundamental del universo.

Referencias

[1] Galería de aplicaciones de COMSOL: Diffraction Patterns
[2] Centro de aprendizaje de COMSOL: Modeling with Partial Differential Equations in COMSOL Multiphysics