Cómo usar estimación de máxima verosimilitud para la estimación de parámetros en COMSOL®
- Detalles
- Categoría: Comsol
- Visto: 5583
Kristian Ejlebjerg Jensen, ingeniero de COMSOL nos explica en este artículo del blog de COMSOL cómo utilizar la estimación por máxima verosimilitud para estimar con el mínimo error los parámetros de la simulación minimizando la diferencia entre los resultados experimentales medidos y los datos correspondientes en el modelo.
Nos recuerda que el método de mínimos cuadrados es un caso especial de estimación de parámetros de máxima verosimilitud que es un buen punto de partida para la estimación de parámetros básicos, lo que lo convierte en un enfoque popular. El software COMSOL Multiphysics® viene con soporte integrado para el método de mínimos cuadrados y en su publicación en el blog de COMSOL nos muestra cómo utilizar la estimación de parámetros de máxima verosimilitud puede ayudar a evitar la necesidad de ajustar manualmente los pesos para un problema determinado.
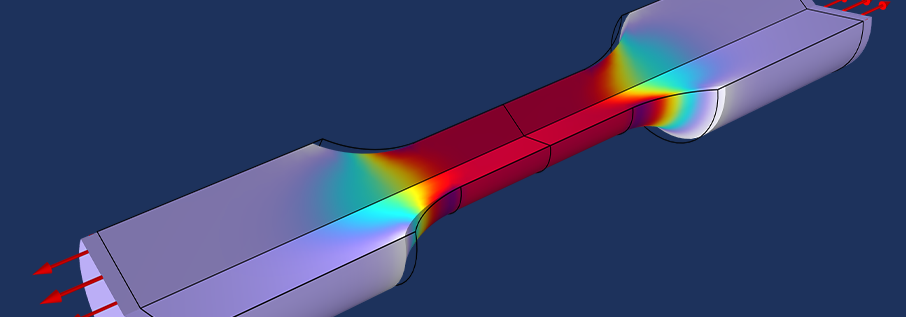
El modelo de ejemplo muestra cómo estimar el módulo de Young y la relación de Poisson en función de una prueba de tracción. El ensayo mide la fuerza de tracción y el desplazamiento radial. Los valores numéricos típicos de estas cantidades difieren en alrededor de 10 órdenes de magnitud. El uso de una estrategia de máxima verosimilitud junto con controles separados para el ruido de cada tipo de datos permite eliminar los parámetros de ponderación.
Nos recuerda que el método de mínimos cuadrados es un caso especial de estimación de parámetros de máxima verosimilitud que es un buen punto de partida para la estimación de parámetros básicos, lo que lo convierte en un enfoque popular. El software COMSOL Multiphysics® viene con soporte integrado para el método de mínimos cuadrados y en su publicación en el blog de COMSOL nos muestra cómo utilizar la estimación de parámetros de máxima verosimilitud puede ayudar a evitar la necesidad de ajustar manualmente los pesos para un problema determinado.
El modelo de ejemplo muestra cómo estimar el módulo de Young y la relación de Poisson en función de una prueba de tracción. El ensayo mide la fuerza de tracción y el desplazamiento radial. Los valores numéricos típicos de estas cantidades difieren en alrededor de 10 órdenes de magnitud. El uso de una estrategia de máxima verosimilitud junto con controles separados para el ruido de cada tipo de datos permite eliminar los parámetros de ponderación.

