por Walter Frei

Cuando se resuelven problemas de ondas electromagnéticas, es probable que se desee modelar un dominio con contornos abiertos — o sea, un contorno del dominio computacional a través del que una onda electromagnética pasará sin reflexión alguna. COMSOL Multiphysics ofrece varias soluciones para esto. Hoy, veremos como utilizar condiciones de contorno de dispersión y capas perfectamente acopladas para truncar dominios y discutiremos sus respectivas ventajas.

¿Por qué truncar el dominio?

A menudo estamos interesados en modelar un objeto radiante, como una antena, en el espacio libre. Podemos construir este modelo para simular una antena en un satélite en el espacio profundo o, más a menudo, una antena montada en una cámara anecoica de prueba.

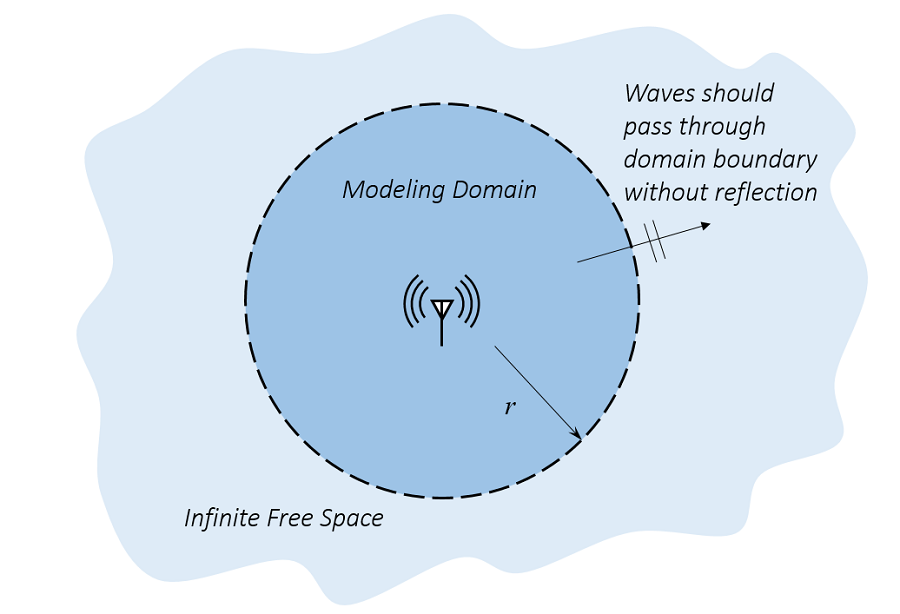
Una antena en el espacio libre. Solo queremos modelar una pequeña región alrededor de la antena.

Este tipo de modelos puede ser construido utilizando la formulación de ondas electromagnéticas en el dominio de la frecuencia del módulo RF o el Wave Optics Module. Estos módulos proporcionan interfaces similares para resolver la forma en el dominio de la frecuencia de las ecuaciones de Maxwell a través del método de los elementos finitos. (Para una descripción de las diferencias clave entres estos módulos, por favor, ver la entrada del blog titulado Computational Electromagnetics Modeling, Which Module to Use?)

En esta entrada del blog nos vamos a limitar a considerar únicamente problemas 2D, donde las ondas electromagnéticas se propagan en el plano x-y, con el campo eléctrico polarizado en la dirección z. Además consideraremos que nuestro dominio del modelo es puramente vacío, por lo que las ecuaciones de Maxwell en el dominio de la frecuencia se reducen a:

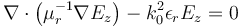
donde 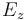es el campo eléctrico, 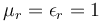la permeabilidad y permitividad relativas en el vacío, y 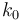es el número de onda.

Resolver la ecuación anterior por el método de los elementos finitos requiere disponer de un dominio de modelado de tamaño finito, así como un conjunto de condiciones de contorno. Queremos utilizar unas condiciones de contorno en el exterior que sean transparentes a cualquier radiación. De esta manera nuestro dominio truncado será una aproximación razonable del espacio libre. También queremos que el dominio truncado sea lo más pequeño posible, ya que mantener nuestro tamaño de modelo pequeño reduce los costes computacionales.

Veamos ahora dos de las opciones disponibles en el entorno de simulació de COMSOL Multiphysics para truncar el dominio del modelo: la condición de contorno de dispersión y la capa perfectamente acoplada.

La condición de contorno de dispersión

Una de las primeras condiciones de contorno transparentes formulada para problemas de ondas fue la condición de radiación de Sommerfeld, que para campos 2D puede escribirse como:

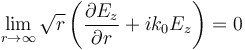
donde r es el eje radial.

Esta condición es exactamente no reflectante cuando las fronteras del dominio de nuestro modelo son infinitamente lejos de nuestra fuente, pero por supuesto un dominio de modelado infinitamente grande es imposible. Así que, aunque no podamos aplicar la condición de Sommerfeld exactamente, podemos aplicar una aproximación razonable de la misma.

Consideremos ahora la condición de contorno:

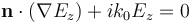
Se pueden ver claramente las similitudes entre esta condición y la condición de Sommerfeld. Esta condición de frontera es llamada, más formalmente, la condición de contorno de dispersión de pimer orden (SBC) y su implementación en COMSOL Multiphysics es trivial. De hecho, no es otra cosa que la condición de contorno de Robin con un coeficiente complejo.

Para ver un ejemplo de una ecuación de onda 2D implementada desde cero junto con esta condición de frontera, vea el modelo de ejemplo de patrones de difracción.

Ahora, existe una limitación significativa a esta condición. Sólo es no reflectiva si la radiación incidente es exactamente normal a la frontera. Cualquier onda que incida sobre la SBC con un ángulo de incidencia no normal será reflejada parcialmente. Más abajo se muestra el coeficiente de reflexión para una onda plana incidente sobre un SBC de primer orden en un ángulo variable.

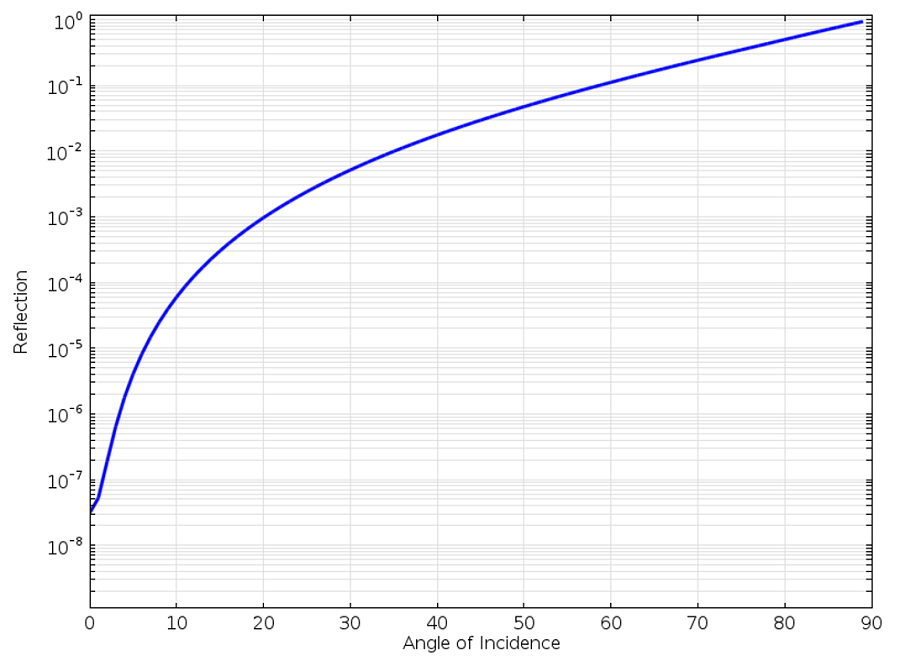
Reflexión de una onda plana en el SBC de primer orden respecto al ángulo de incidencia.

Podemos observar del gráfico anterior que a medida que la onda plana incidente se aproxima a la incidencia rasante, la onda es prácticamente reflejada completamente. A un ángulo de incidencia de 60º, la reflexión es aproximadamente del 10%, así que claramente querremos disponer de una condición de contorno mejor.

COMSOL Multiphysics también incluye (desde la versión 4.4) el SBC de segundo orden:

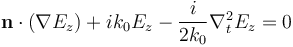
Esta ecuación incluye un término de segundo orden, que toma la segunda derivada tangencial del campo eléctrico en la frontera. Esto también es bastante fácil de implementar en la arquitectura del software COMSOL.

Comparemos los coeficientes de reflexión de los SBC de primer y segundo orden:

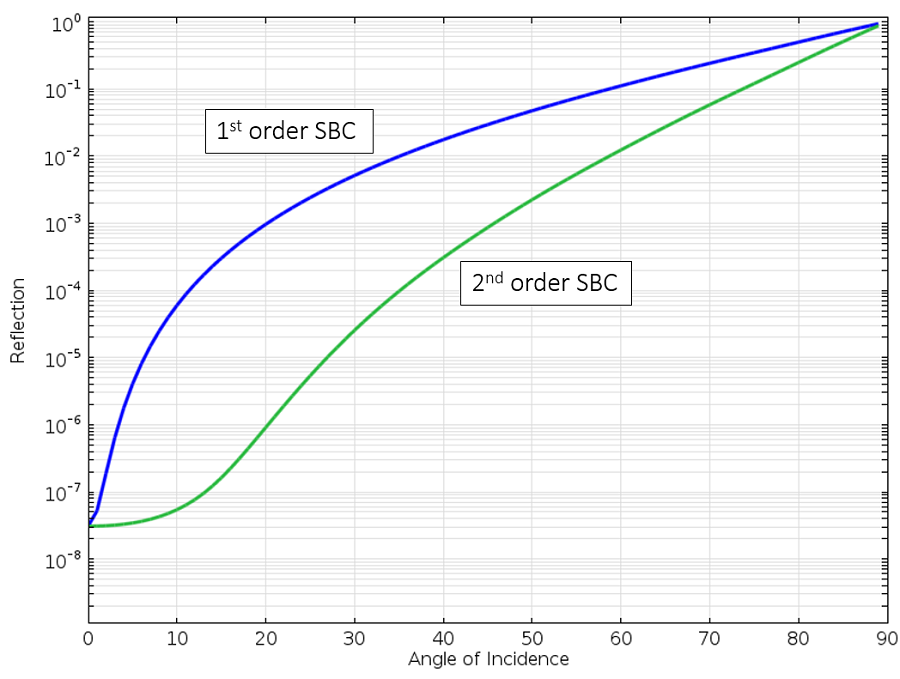
Reflexión de una onda plana en el SBC de primer y segundo orden respecto al ángulo de incidencia.

Podemos ver que el SBC de segundo orden es uniformemente mejor. Podemos llegar a un ángulo de incidencia de ~75° antes de que la reflexión sea del 10%. Es mejor, pero todavía no lo mejor que podemos obtener. Fijemos ahora nuestra atención lejos de las condiciones de contorno y veamos las capas perfectamente acopladas.

La capa perfectamente acoplada

Recordemos que estamos intentando simular una situación como la de una antena en una cámara anecoica, una habitación con cuñas piramidales de material absorbente a la radiación en las paredes que minimizará cualquier señal reflejada. Esta podría ser nuestra analogía física para la capa perfectamente acoplada (PML), que no es una condición de contorno, sino más bien un dominio que añadimos en el exterior del modelo, que debería absorber todas las onas salientes.

Matemáticamente hablando, la PML es simplemente un dominio que tiene unas permitividad y permeabilidad complejas y anisotrópicas. Para un ejemplo de una derivación completa de estos tensores, por favor, vea por ejemplo la referencia "Theory and Computation of Electromagnetic Fields". Aunque los PML son teóricamente no reflectantes, muestran cierta reflexión debido a la discretización numérica: la malla. Para minimizar esta reflexión, queremos utilizar una malla en la PML que se alinee con la anisotropía en las propiedades del material. Debajo se muestran las mallas PML adecuada, para dominios circular 2D y esféricos 3D. Las PML cartesianas y esféricas y su uso apropiado también se discuten en la documentación del producto.

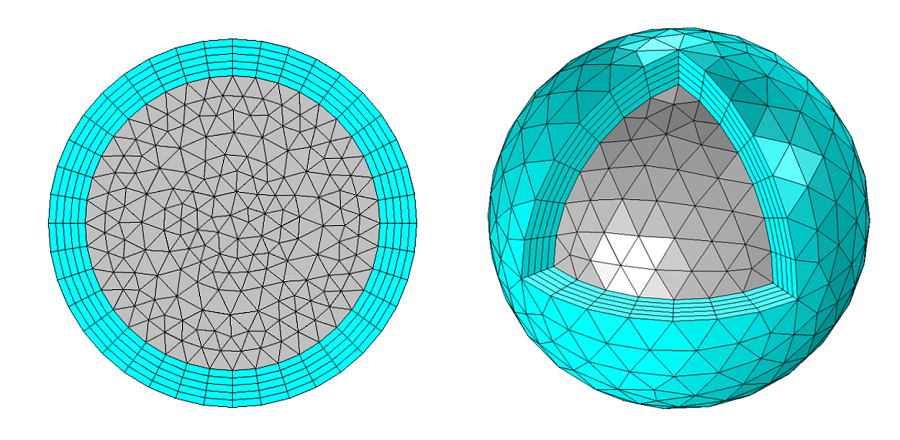
Mallas apropiadas para PML esférica 2D y 3D.

En COMSOL Multiphysics 5.0, estas mallas pueden configurarse automáticamente para problemas 3D utilizando el mallado controlado por la física, como se demuestra en este vídeo.

Veamos ahora la reflexión en una PML respecto al ángulo incidente en comparación con las SBC:

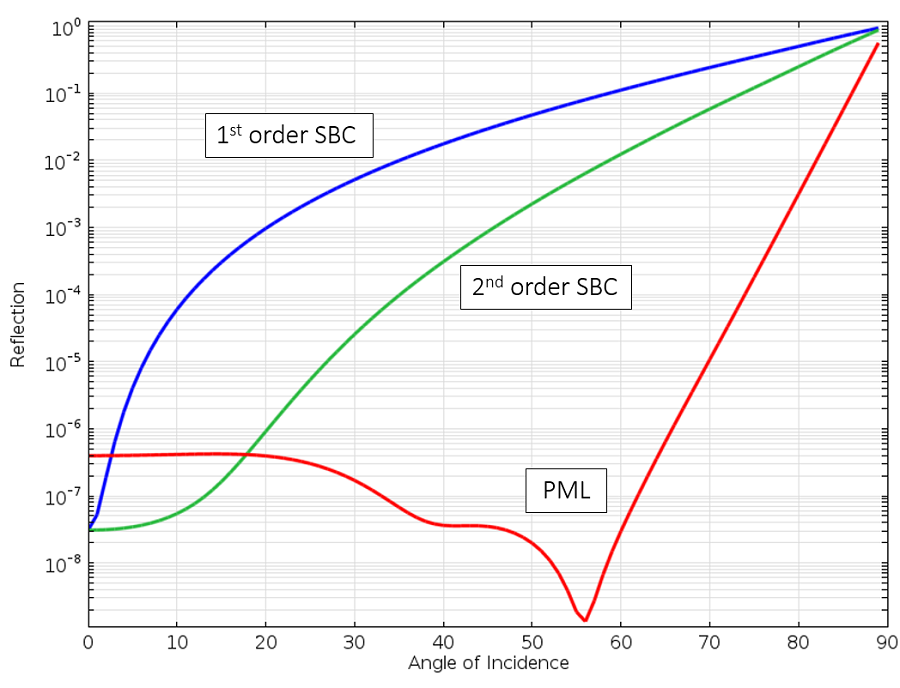
Reflexión de una onda plana en SBC de primer y segundo orden y en la PML respecto al ángulo de incidencia.

Podemos ver que la PML refleja la menor cantidad en el rango más amplio. Todavía existe reflexión cuando la onda se propaga prácticamente paralela a la frontera, pero estos casos son bastante raros en la práctica. Una funcionalidad adicional de la PML, que ahora no veremos en profundidad, es que absorbe no solo la onda propagada, sino también cualquier campo evanescente. Así que desde un punto de vista físico, la PML realmente puede pensarse como un material con absorción prácticamente perfecta.

¿Entonces, qué opción debería utilizar?

Claramente, la PML es la mejor de las aproximaciones descritas aquí. Sin embargo, la PML utiliza más memoria en comparación con los SBC. Así que, si se está en las etapas tempranas del proceso de modelado y se quiere construir un modelo que sea un poco menos intensivo computacionalmente, el SBC de segundo orden es una buena opción. También se puede utilizar en situaciones donde se tenga una razón importante para creer que cualquier reflexión en el SBC no afectará en gran medida los resultados en los que se está interesado.

El SBC de primer orden es en la actualidad el método por defecto, por razones de compatibilidad con versiones previas del software, pero con COMSOL Multiphysics versión 4.4 o superior, mejor utilizar SBC de segundo orden. Aquí solo hemos hablado de la forma de onda plana del SBC, pero también están disponibles formas de onda cilíndrica y esférica (en 3D) de los SBC de primer y segundo orden. Aunque utilizan menos memoria, todos presentan mayor reflexión en comparación con la PML.

Los SBC y las PML son condiciones apropiadas para contornos abiertos donde no se sabe mucho, a priori, de los campos en las fronteras. Si, por otro lado, se quiere modelar un contorno abierto donde se sabe que los campos tienen una cierta forma, como un contorno que represente a una guía de onda, las condiciones de contorno de Puerto y Pueto Balanceado son más apropiadas. Veremos estas condiciones más adelante en una entrada del blog.