video Taller: Experimentar en Matemáticas con Maple (17 de junio de 2021)

Etiquetado en Conjetura de Casas-Alvero, cuádricas, experimentación, investigación, Maple, Maple 2021, matemáticas, matrices bohemias

Taller: Experimentar en Matemáticas con Maple (17 de junio de 2021)

La disponibilidad de herramientas como Maple ha permitido introducir la componente experimental dentro de la investigación que hacemos en Matemáticas. El objetivo de este taller es presentar tres ejemplos concretos donde la utilización de Maple ha sido esencial para poder descubrir, conjeturar y, en algunos casos, demostrar nuevas propiedades de los objetos matemáticos que se estaban analizando.

En el primer ejemplo mostraremos cómo el uso de Maple permitió proporcionar los primeros resultados no triviales sobre la Conjetura de Casas-Alvero que pregunta si todo polinomio que tenga una raíz en común con cada una de sus derivadas (no siempre la misma) es forzosamente una potencia de un factor lineal. Se puede encontrar más información en:

  • G.M. Diaz-Toca y L. Gonzalez-Vega: On analyzing a conjecture about univariate polynomials and their roots by using maple. Proceedings of the Maple Conference 2006, 81-98, 2006.
  • W. Castryck, R. Laterveer y M. Ounaïes: Constraints on counterexamples to the Casas-Alvero conjecture and a verification in degree 12. Mathematics of Computation 83, 3017-3037, 2014.

En el segundo ejemplo mostraremos cómo el uso de Maple permitió describir la estructura de la ecuación implícita de la proyección de la curva de intersección entre dos cuádricas 3D. Por ejemplo, sin la ayuda de Maple y entre otras propiedades, hubiera sido muy complicado demostrar que su grado es siempre menor o igual que 8 cuando, en principio, podría llegar a tener hasta 12. Se puede encontrar más información en:

  • L. Gonzalez-Vega y A. Trocado: Tools for analyzing the intersection curve between two quadrics through projection and lifting. Journal of Computational and Applied Mathematics 393,113522, 2021.

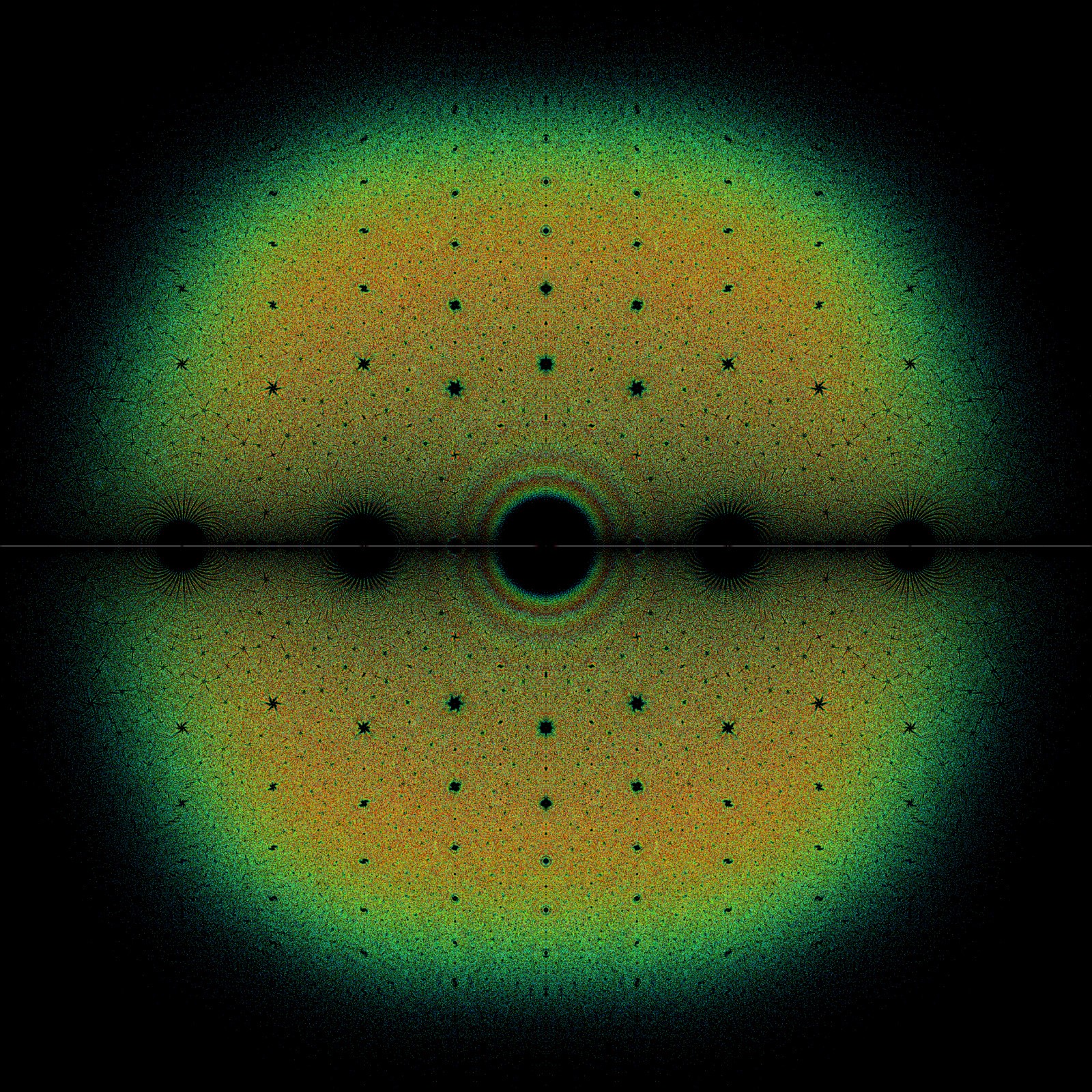
Finalmente, en el último ejemplo, mostraremos cómo el uso de Maple ha sido esencial en el estudio de las propiedades las denominadas matrices bohemias, matrices cuyas entradas pertenecen a un conjunto finito de valores (por ejemplo, -1, 0 y 1). Sin la ayuda de Maple hubiera sido imposible llegar a resultados sobre el comportamiento asintótico de los autovalores de las matrices bohemias partiendo de figuras como la que acompaña a este texto, donde se visualizan los autovalores de todas las matrices 5x5 cuyas entradas son, o -1, o 0, o 1 (el color se asigna en función de la densidad con la que aparece cada autovalor). Se puede encontrar más información en: