Por Josué Zable.

Anteriormente escribí que los especialistas en marketing deben conocer (al menos) un método estadístico básico para realizar correctamente las pruebas A/B. Con suerte, con algunos conocimientos en su haber, dejará de permitir que la ansiedad por las estadísticas le frene en su carrera de marketing y emprenderá una tarea un poco más desafiante: las pruebas A/B/C.

¿QUÉ SON LAS PRUEBAS A/B/C?

Las pruebas A/B/C, al igual que las pruebas A/B, son una forma de experimento controlado. En el caso de A/B/C, está probando más de dos versiones (por lo tanto, agrega la “C” a A/B) de una variable (página web, elemento de página, correo electrónico, etc.). Esto se puede usar para comparar 3 o más versiones de algo para determinar qué versión funciona mejor, como enviar varios correos electrónicos para ver cuál genera más participación o usar diferentes anuncios para medir las tasas de clics. Un caso de uso común es desafiar un grupo estándar o de control contra múltiples variantes. Por ejemplo, probar una página web actual con dos diseños de página web alternativos para ver qué diseño genera más conversiones, el original o los dos rivales.

Como escribimos antes, hay muchas pruebas diferentes que puedes ejecutar, incluidas herramientas que prueban múltiples componentes al mismo tiempo. Hoy veremos una prueba A/B/C simple, comparando tres versiones en una sola medición. Podrían ser tasas de apertura o tasas de clics en correos electrónicos, anuncios o páginas web.

INTRODUCCIÓN A LA REGRESIÓN LOGÍSTICA BINARIA

El análisis de regresión logística binaria se utiliza para describir la relación entre un conjunto de predictores y una respuesta binaria. Una respuesta binaria tiene dos resultados, como aprobado o reprobado. En marketing, esto a menudo se traduce en clics, aperturas o conversiones. Cuando solo se comparan dos enfoques, existen métodos más simples, como la prueba de dos proporciones.

UN EJEMPLO DE PRUEBA A/B/C

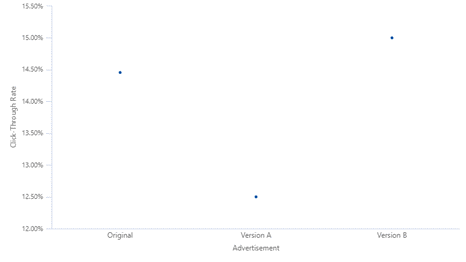
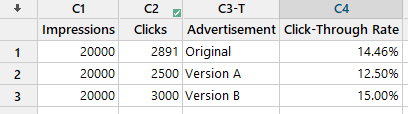
Imagine que un especialista en marketing ejecuta una campaña publicitaria periódica en las redes sociales para atraer visitantes a su sitio web. Deciden ejecutar una prueba A/B/C con diferentes versiones del anuncio para ver qué anuncio generará más clics. Apuntan a 20.000 impresiones para cada anuncio y realizan su prueba. Recopilan sus resultados y los grafican. Según el gráfico de valores individuales, está claro que la Versión A tuvo un peor desempeño que la Original y la Versión B. La pregunta sigue siendo: ¿son las diferencias estadísticamente significativas para alejarse del original?

REGRESIÓN LOGÍSTICA BINARIA PARA ANALIZAR LA PRUEBA

Con los datos recopilados, puedo usar Minitab para ajustar un modelo de regresión logística binaria.

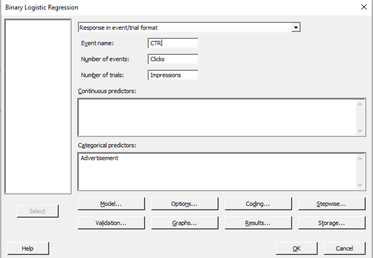
Al ir a Estadísticas > Regresión > Regresión logística binaria > Ajustar modelo logístico binario, Minitab presenta una ventana de diálogo para que seleccione “Respuesta en formato de evento/ensayo” y complete mis eventos (clics) y ensayos (impresiones). ¡También selecciono Publicidad como elemento que estoy probando y dejo que Minitab cree mi modelo!

CONCLUSIONES DEL ANÁLISIS DE LOS RESULTADOS

Ahora necesitamos profundizar un poco en las estadísticas (¡no mucho, solo un poco! Estás aquí para aprender algo, ¿no?). Mirando la tabla a continuación, vemos el Odds Ratio que compara las probabilidades de dos eventos, en nuestro caso haciendo clic en los diferentes anuncios. Minitab configura la comparación enumerando los niveles en 2 columnas, Nivel A y Nivel B. El nivel B es el nivel de referencia para el factor. Los índices de probabilidad superiores a 1 indican que el evento, en nuestro caso los clics, es más probable en el nivel A. Los índices de probabilidad inferiores a 1 indican que es menos probable que se produzca un clic en el nivel A.

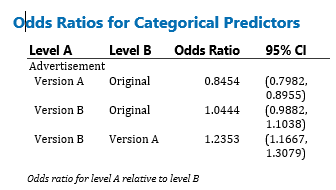
Con respecto a nuestra tabla, al comparar la Versión A con la Original, un Odds Ratio inferior a 1 significa que es menos probable que se produzca un clic en la Versión A. Al seguir la tabla, vemos que es más probable que la Versión B obtenga un clic que la Versión B. tanto el original como la Versión A. Esto valida lo que graficamos y comparamos, pero ¿dónde está la información adicional?

Al observar la segunda columna, Intervalo de confianza del 95 %, obtenemos información adicional sobre nuestros datos. En este tipo de análisis, los intervalos de confianza que contienen 1 dentro de su rango (como la versión B frente a la original, donde el IC del 95 % es 0,9882,1,1038) indican que las probabilidades de hacer clic o no hacer clic son esencialmente las mismas para los dos grupos.

Como resultado, esta prueba nos ha enseñado que, sin lugar a dudas, la Versión A es el anuncio con peor rendimiento y no vale la pena conservarlo. Sin embargo, sería un error sustituir automáticamente la versión B por la original. Nuestros próximos pasos deberían ser a) refinar nuestra prueba a una prueba A/B comparando el Original con la Versión B o b) seleccionar el Original o la Versión B por razones cualitativas como "seguir con nuestro mensaje consistente" o "actualizar nuestro mensaje". sin preocuparse por comprometer los resultados.