La pruebas de hipótesis es un procedimiento esencial en estadística. Una prueba de hipótesis evalúa dos afirmaciones mutuamente excluyentes sobre una población para determinar qué afirmación es mejor admitida por los datos de la muestra. Cuando se dice que un hallazgo es estadísticamente significativo, es gracias a una prueba de hipótesis. ¿Cómo funcionan realmente estas pruebas y qué significa realmente significación estadística?

En esta serie de artículos se ayudará a comprender de forma intuitiva cómo funcionan las pruebas de hipótesis al centrarse en conceptos y gráficos en lugar de ecuaciones y números. Después de todo, una razón clave para utilizar un software estadístico como Minitab es no quedarse atascado en los cálculos, y, en cambio, poder concentrarse en comprender sus resultados.

Para comenzar el tema en este artículo, resaltamos la razón para utilizar pruebas de hipótesis con un ejemplo.

El escenario

Un economista quiere determinar si el coste mensual de energía para las familias ha cambiado con respecto al año anterior, cuando el coste promedio mensual fue de 260$. El economista toma muestras aleatorias de 25 familias y registra sus costos de energía para el año en curso. (Los datos para este ejemplo son CostEnergFamilia y es solo uno de los muchos conjuntos de datos de ejemplo que se pueden encontrar en la Biblioteca de conjuntos de datos de Minitab.)

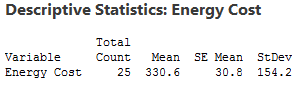
Estas estadísticas descriptivas se utilizarán para crear un gráfico de distribución de probabilidad que muestra la importancia de las pruebas de hipótesis.

La necesidad de pruebas de hipótesis

¿Por qué se necesitan pruebas de hipótesis? Después de todo, tomamos una muestra aleatoria y nuestra media de la muestra de 330.6 es difernte de 260. Es diferente ¿verdad? Desafortunadamente, el panorama es confuso porque se está viendo una muestra en lugar de toda la población.

El error de muestreo ese la diferencia entre una muestra y toda la población. Gracias al error de muestreo, es totalmente posible que mientras nuestra media muestral sea 330.6, la media poblacional aún sea 260. O dicho de otra manera, si se repite el experimento, es posible que la segunda media muestral esté cerca de 260 ¡Una prueba de hióptesis ayuda a evaluar la probabilidad de esta posibilidad!

Utilizar la distribución del muestreo para ver si la media muestra es poco probable

Para cualquier muestra aleatoria dada, la media de la muestra casi seguro que no es igual a la media real de la población debido al error de muestreo. Para este ejemplo, es poco probable que el coste promedio para toda la población sea exactamente 330.6. De hecho, si tomamos múltiples muestras aleatorias del mismo tamaño de la misma población, podríamos trazar una distribución de las medias muestrales.

Una distribución muestral es la distribución de una estadística, como la media, que se obtiene al extraer repetidamente un gran número de muestras de una población específica. Esta distribución le permite determinar la probabilidad de obtener el estadístico de la muestra.

Afortunadamente, se puede crear una gráfica de medias de muestras sin recolectar muchas muestras aleatorias diferentes. En su lugar se crea un gráfico de distribución de probabilidad utilizando la distribución t, el tamaño de la muestra y la variabilidad en nuestra muestra para representar gráficamente la distribución muestral.

Nuestro objetivo es determinar si la media de la muestra es significativamente diferente de la media de hipótesis nula. Por lo tanto, usaremos el gráfico para ver si nuestra media muestral de 330.6 es poco probable, suponiendo que la media poblacional es 260. La muestra siguiente muestra la distribución esperada de las medias muestrales.

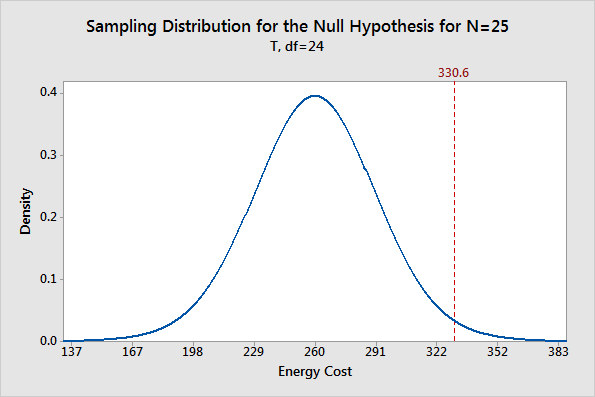
Se puede ver que la media muestral más probable es 260, lo que tiene sentido porque suponemos que la hipótesis nula es cierta. Sin embargo, existe una probabilidad razonable de obtener una media muestral que oscila entre 167 y 352, e incluso más allá. El resultado de este gráfico es que aunque nuestra media muestral de 330.6 no es la más probable, tampoco está fuera del ámbito de lo posible.

El papel de las pruebas de hipótesis

Hemos colocado la media muestral en el contexto de todas las medias muestrales posibles, asumiendo que la hipótesis nula es cierta. ¿Son estos resultados estadísticamente significativos?

Como puede verse, no hay un lugar mágico en la curva de distribución para hacer esta determinación. En cambio, existe una disminución continua en la probabilidad de obtener medias muestrales que están más lejos del valor de la hipótesis nula. ¿Dónde trazamos la línea?

Aquí es donde las pruebas de hipótesis son útiles. Una prueba de hipótesis permite cuantificar la probabilidad de que nuestra media muestral sea inusual.

En esta serie de publicaciones se continuará utilizando este marco gráfico y se añadirá el nivel de significación, el valor de P y el intervalo de confianza para mostrar cómo funcionan las pruebas de hipótesis y qué significa realmente la significación estadística.

• Parte Dos: Intervalos de confianza y niveles de confianza
• Parte Tres: Niveles de significancia (alpha) y P valores