Por Bruno Scibilia (Traducido del blog de Minitab)

Estamos en una era de datos masivos. Se está generando una gran cantidad de datos de la web y de registros de relaciones de clientes, sin mencionar también los procedentes de los sensores utilizados en la industria productiva (empresas de semiconductores, farmacéuticas, petroquímicas y muchas otras industrias).

Gráficos de control univariable

En la industria manufacturera las características críticas de los productos son recogidos rutinariamente para asegurar que todos los productos en cada paso del proceso se mantienen dentro de las especificaciones. Los gráficos de control univariable dedicados se utilizan para asegurar que cualquier deriva es detectada cuanto antes para evitar efectos negativos en el rendimiento del producto final. De forma ideal, cuando se identifica una causa especial, la maquinaria debería de ser parada inmediatamente hasta que se resuelva el problema.

Monitorización de los parámetros del proceso de las herramientas

En las plantas modernas, muchas herramientas de producción se conectan a redes IT de forma que los parámetros del proceso de esa herramienta pueden registrarse y almacenarse en tiempo real (presiones, temperaturas, etc.) Desgraciadamente, este tipo de datos, muy a menudo no se monitorizan continuamente, aunque se puede esperar que esos parámetros del proceso jueguen un importante papel en términos de la calidad final del producto. Cuando ocurre un incidente de calidad, a menudo se recuperan los datos de esos numerosos parámetros del proceso de la base de datos para investigar (después del hecho) por qué tuvo lugar ese incidente.

Una aproximación más eficiente sería monitorizar esos parámetros del proceso en tiempo real e intentar comprender cómo afectan a los complejos procesos de fabricación: ¿Qué parámetros del proceso son realmente importantes y cuáles no? ¿Cuáles son sus valores de mejor ajuste?

Gráficos de control multivariable

Sin embargo, monitorizar los parámetros de las herramientas a medida que se avanza en el proceso podría llevar a un inmenso incremento en el número de gráficos de control. En este contexto, los ingenieros de procesos podrían beneficiarse del uso de gráficos multivariable que permiten monitorizar hasta 7 u 8 parámetros juntos en un único gráfico. En vez de utilizar datos de parámetros de los procesos de los equipos para investigar las causas de incidentes previos de calidad en un modo de equipos de intervención, esta aproximación se centraría en mejoras de largo término.

Los gráficos de control multivariable se basan en distancias cuadráticas multivariables estandarizadas (generalizadas) de la media general. En Minitab, el método T² Hotelling se utilize para generar gráficos multivariable. Si todavía no dispone de Minitab y desea probar de crear algunos de estos gráficos sobre los que estamos hablando, puede descargar la versión de evaluación de 30 días.

Una ventaja obvia de utilizar gráficos multivariable es que permiten minimizar el número total de gráficos de control que se necesitan gestionar, pero existen también otras ventajas relacionadas adicionales involucradas:

• Analizar conjuntamente parámetros del proceso: Muchos parámetros del proceso están relacionados con otros, por ejemplo, para un paso particular del proceso podríamos esperar que el valor de la presión sea grande cuando la temperatura es alta. Considerar cada parámetro del proceso por separado no tiene por qué ser una buena opción e incluso podría ser engañoso. Detectar cualquier desajuste entre los ajustes de los parámetros puede ser de gran utilidad.
  
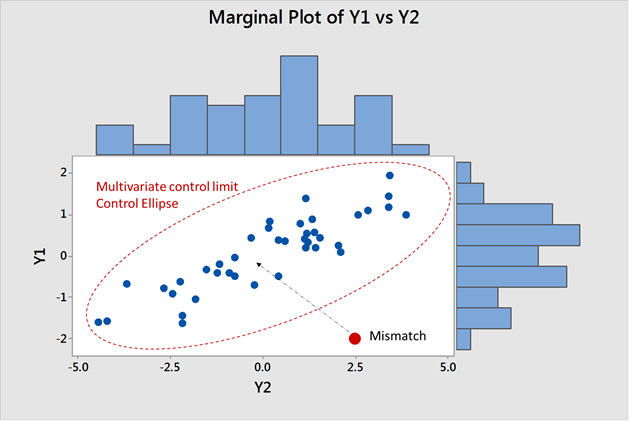
  En el gráfico inferior, los valores de los parámetros Y1 y Y2 están correlados (altos valores de Y1 están asociados con altos valores para Y2) así que el punto rojo en la esquina inferior derecha parece estar fuera de control (fuera de la elipse de control) desde un punto de vista multivariable. Sin embargo, desde una perspectiva univariable, este punto rojo permanece dentro de los márgenes de fluctuación usuales tanto para Y1 como Y2. Este punto claramente representa un desajuste entre Y1 y Y2. La distancia cuadrática multivariable generalizada del punto rojo a la media de la nube de puntos es inusitadamente grande.
  
  
• Tasa global de falsas alarmas: La probabilidad de una falsa alarma con límites estándar tres-sigma en un gráfico de control es 0,27%. Si se monitorizan 100 gráficos al mismo tiempo, la probabilidad de una falsa alarma automáticamente aumenta al 27% (0.27% * 100).
  
  Sin embargo, cuando se monitorizan simultáneamente numerosas variables utilizando un gráfico multivariable, la tasa global/familiar de falsas alarmas permanece cercana al 0.27%.
• Medidas 3-D: Cuando se toman medidas tridimensionales de un product, la cantidad de datos necesarios para asegurar que todas las dimensiones (X, Y y Z) permanecen dentro de las especificaciones puede ser realmente grande. Pero si el producto queda dañado en una zona particular, esto normalmente afecta a más de una dimension, por lo que las tres dimensiones no deberían de considerarse por separado. Si un gráfico multivariable monitoriza simultáneamente las desviaciones de los valores X, Y, Z planeadas, serán tenidos en cuenta sus efectos combinados.

Un sencillo ejemplo

Se han monitorizado ocho parámetros del proceso utilizando ocho gráficos de control Xbar univariable. No se ha detectado ningún punto fuera de control (ver debajo):

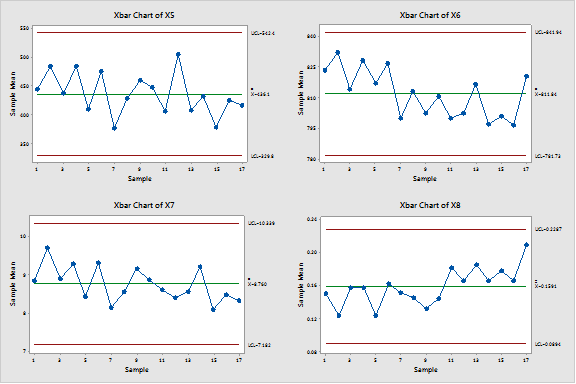
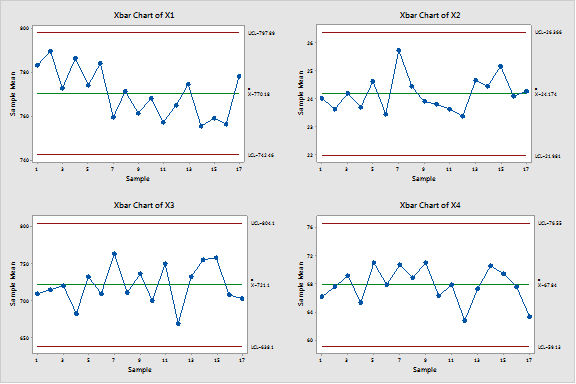
Los ocho gráficos de control anteriores pueden reemplazarse por un único gráfico multivariable que monitorice las ocho variables simultáneamente. Aunque no se detectó ningún punto fuera de control en los gráficos univariable, el subgrupo número 12 resulta estar fuera de control en el gráfico multivariable:

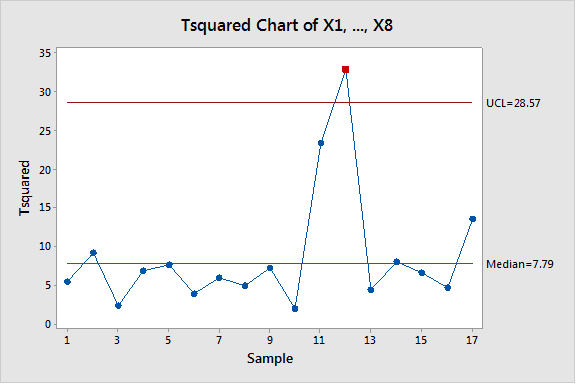
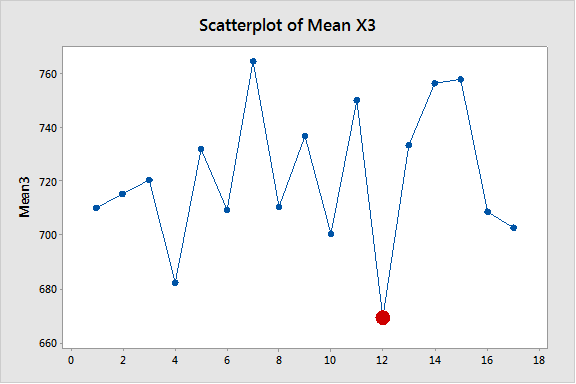
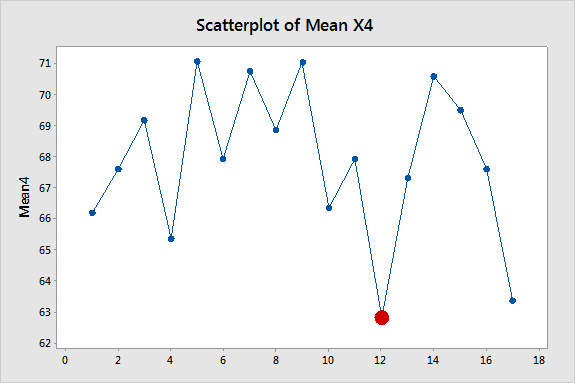
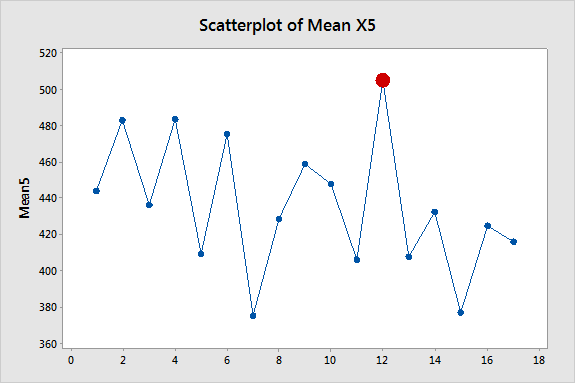
Para investigar por qué ocurrió un punto fuera de control (subgrupo 12) en el gráfico multivariable, utilizamos unos sencillos gráficos (gráficos de dispersión) para analizar las tendencias temporales. Nótese que en lo que respecta a donde están involucrados los parámetros X3, X4 y X5, el subgrupo 12 está posicionado lejos de los otros puntos.

Conclusión

Cuando los parámetros del proceso no tienen un efecto crítico directo, no se requiere necesariamente un gráfico univariable dedicado. Los gráficos multivariable permiten monitorizar rutinariamente muchos parámetros del proceso de las herramientas con menos gráficos. El objetivo sería comprender mejor cuándo pueden utilizarse puntos fuera de control en un gráfico multivariable para prever problemas de calidad relativas a las características del producto.

Para controlar major un proceso, necesitamos evaluar cómo afectan los parámetros de las herramientas que vamos utilizando sobre el producto final. Los gráficos multivariable también son de gran utilidad para monitorizar medidas 3D. Identificar la razón por la que existe un punto fuera de control en un gráfico multivariable es un aspecto clave para utilizarlo con éxito.