Simulación de la dinámica de evolución en poblaciones finitas con Mathematica
- Detalles
- Categoría: Mathematica
- Visto: 3590
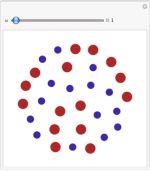
En poblaciones finitas, la dinámica de evolución no puede ser descrita a partir de ecuaciones diferenciales deterministas; su descripción requiere la formulación estocástica.
Bernhard Voelkl explica en su artículo Simulation of Evolutionary Dynamics in Finite Populations publicado en el volumen 13 de The Mathematica Journal cómo Mathematica puede ser utilizado tanto para simular como para visualizar procesos evolucionarios en poblaciones limitadas. El proceso de Moran se introduce como el modelo estocástico básico de un proceso de evolución en poblaciones finitas. Este modelo es extendido a poblaciones mixtas con diferencias de ajuste relativo. En el artículo, el autor combina ecología de poblaciones con ideas de teoría de juegos, para simular jeugos de evolución en poblaciones estructuradas y bien mezcladas.
El artículo se puede consultar en la propia web y también se puede descargar en formato notebook de Mathematica y PDF.
Bernhard Voelkl explica en su artículo Simulation of Evolutionary Dynamics in Finite Populations publicado en el volumen 13 de The Mathematica Journal cómo Mathematica puede ser utilizado tanto para simular como para visualizar procesos evolucionarios en poblaciones limitadas. El proceso de Moran se introduce como el modelo estocástico básico de un proceso de evolución en poblaciones finitas. Este modelo es extendido a poblaciones mixtas con diferencias de ajuste relativo. En el artículo, el autor combina ecología de poblaciones con ideas de teoría de juegos, para simular jeugos de evolución en poblaciones estructuradas y bien mezcladas.
El artículo se puede consultar en la propia web y también se puede descargar en formato notebook de Mathematica y PDF.

